无线传感器网络的定位改进算法

雷景生，郝阳阳，郝 伟

(1.上海电力学院 电子与信息工程学院，上海 200090;2.63870部队 测试站电测兼容测试室，陕西 华阴 714200)

无线传感器网络是一种分布式的自组织网络.在无线传感器网络绝大多数的应用中，节点的位置信息和感知信息同等重要，没有位置信息的感知数据是没有实际意义的.传感器节点自身的正确定位使待定位事件位置信息得到保障，也就是说，在传感器节点自身正确定位的前提下，才可以定位待定位节点事件的实际位置.因此，节点的有效定位成为无线传感器网络应用需要考虑的重要因素之一.

目前，国内外已经提出了很多优化传感器网络节点定位算法.DV-Hop算法是通过一个锚节点到待定位节点的最小跳数乘以平均跳距估计待定位节点和锚节点之间的距离.然而节点分布不均，相邻节点之间的距离实际差异不能真正反映平均跳距离，甚至有一些实际的距离，相邻节点与平均跳距相差很大.[1]所以当节点分布不均匀时，DV-Hop算法的测距误差较大，从而使定位精度受到影响.而且针对测距误差已经有了很多的改进方法，[2-3]虽然误差有所降低，[4]但都不是很理想.因此，本文在原有DV-Hop算法的基础上进行加权改进，提出了一种新的误差较小的节点精确定位算法.

1 经典DV-Hop算法分析

DV-Hop定位算法包括3个过程.

第一步 通过典型的距离矢量交换协议，网络中的每个参考节点向邻居节点传播自身位置信息的分组，使得网络中的所有节点获得距离参考节点的最小跳数信息.然后对跳数值加1，并转发到邻居节点.通过此方法可以得到网络中每个锚节点的最小跳数.

第二步 利用其他参考节之间的最小跳数和位置信息，让每个参考节点求出平均跳距，然后将平均跳距当作校正值传播至网络.当未知节点收到校正值后，以跳数为根据可以计算出其与参考节点之间的距离.

利用其他参考节点之间的最小跳数和位置信息，使每一个参考节点得到平均跳距，然后将平均跳距的平均传播作为网络的校正值，再对跳数进行校正，每个节点根据参考节点之间的距离进行计算.通过第一步中的校正值，利用式(1)来估算:

式中:(xi，yi)——第i个节点的坐标;

(xi，yi)——第j个节点坐标;

hij——第i个节点至第j个节点的跳数.

DV-Hop 的模型如图 1 所示.例如，Q1，Q2，Q3分别是信标节点，Q1到 Q2的实际距离S12=24，Q1到p的实际距离为13，Q2到p的实际距离为11，Q1与Q2之间跳数Hops12=5跳;Q2到Q3的距离S23=16，其间的跳数Hops23=3跳.根据 DVHop算法，得出平均跳距Hopsize=(S12+S23)/(Hops12+Hops23)=5.再根据Q1和Q2到未知节点p的跳数分别为2跳和3跳，得到未知节点p到信标节点Q1和Q2的距离分别为d1=10，d2=15.测出的结果与实际结果相差较大，造成误差的原因是节点分布不均匀.即如图1，在算法中，Q1仅用了2跳到达未知节点p.但在实际中，因为节点分布不均匀而并不是2跳，所以导致测试出来的结果有差异.

图1 DV-Hop算法模型

当计算完与一个信标点无关的信标节点每跳的平均距离后，再将邻居节点广播的消息发至分组中，其中包含了周围相邻节点先得到的各信标节点的最新信息.[5]在无线传感器网络中，位置信息以传播的形式发散，当网络节点收到位置信息时将与原来的位置信息进行比较，若收到的位置信息与原来的位置信息不同，就忽略原来的位置信息，将刚收到的位置信息进行储存，这样就可以保证节点只储存一条最新的位置信息.待定位节点收到信标节点每段的平均距离，再由式(2)计算可得到待定位节点到信标节点之间的距离

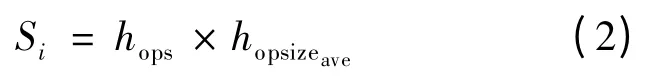
式中:hops——待定位节点到锚节点的最小跳数.

第三步 如果要获得与3个以上参考节点的距离时，可以通过最大似然估计法和最小二乘法来计算待定位节点的位置.

在DV-Hop定位算法中，将跳数的距离与平均每段的跳距作为距离的估算值，因此DV-Hop的定位精度很大程度上取决于平均跳距.如果要将误差保持在合理的估算范围内，则需要无线传感器网络中的节点分布均匀、密集.但在实际的网络中，节点较少且分布离散，这样很容易造成迭代误差.而且随着跳数的增加，误差将会越变越大.

2 DV-Hop算法的改进

针对上述DV-Hop算法的误差分析，下面提出利用mandist和dist分别加权最小二乘法.

在极大似然估计法的定位过程中，一般步骤为:已知信标节点 1，2，3，4，…，n 的坐标分别是(x1，y1)，(x2，y2)，(x3，y3)，…，(xn，yn)，待定位节点C的坐标是(x，y).则由空间坐标计算可知:

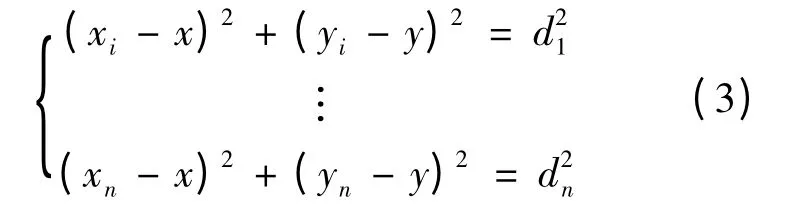
式(3)也可以表示为:

式中:

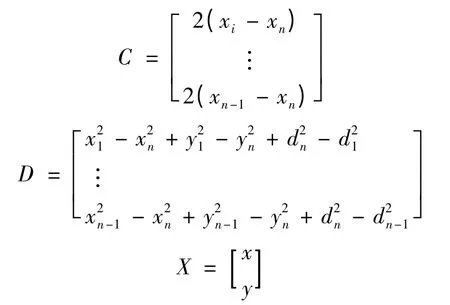
对于方程(4)，由标准的最小均方差的估计法可得到位置节点坐标为:

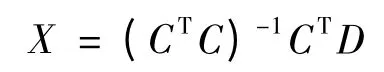
在大型网络中，位置估计误差较大.为了解决迭代误差的问题，可以采用加权最小二乘估计方法，它根据每个信标节点上的最小二乘估计的位置精度定位不同的加权因子来提高定位精度.[6]在实践中，加权系数的误差为协方差.

在实际应用中可知，误差的协方差与加权系数有关.理论上，要使估计误差的方差最小，则加权矩阵w取测量值误差方差矩阵的逆矩阵.然而在实际应用中如何定义w还需要进一步研究.[7]一般情况下，随着节点间的跳数变大时产生的误差也变大，所以加权取值要小一点;而随着节点间的跳数变小时产生的误差会变小，所以加权取值需大一点.

因此，我们需要引入加权系数wi，其中wi=1/hi(hi为参加定位节点与未知节点C之间的最小跳数[8])，再利用曼哈顿距离加权函数mandist和欧氏距离加权函数dist分别加权wi，可以得出

经过加权，利用最小二乘法可得位置节点的坐标为X=(CTWC)－1CTWD.

3 仿真与分析

为了对改进算法性能进行检测，在Matlab平台上分别将 DV-Hop，mandist，dist加权定位算法进行仿真，然后对产生的数据进行对比分析，主要从平均定位误差方面对3种定位算法的性能进行评估.

3.1 训练次数变化分析

仿真网络的参数设计如表1所示.初始节点分布如图2所示.

表1 仿真参数设置

图2 初始节点分布

由dist和mandist加权的最小二乘法定位算法与DV-Hop算法每次定位误差的对比图结果分别如图3和图4所示.由图3和图4可以得出，加权后的定位算法在每次的训练优化后的平均定位误差都分别低于DV-Hop算法.

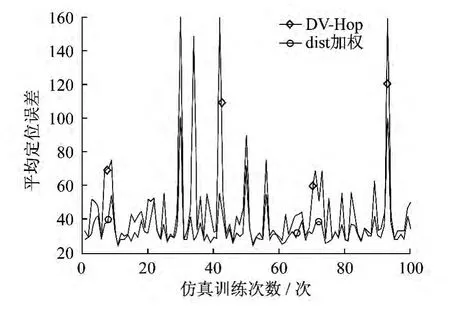
图3 dist加权和DV-Hop算法每次定位误差对比

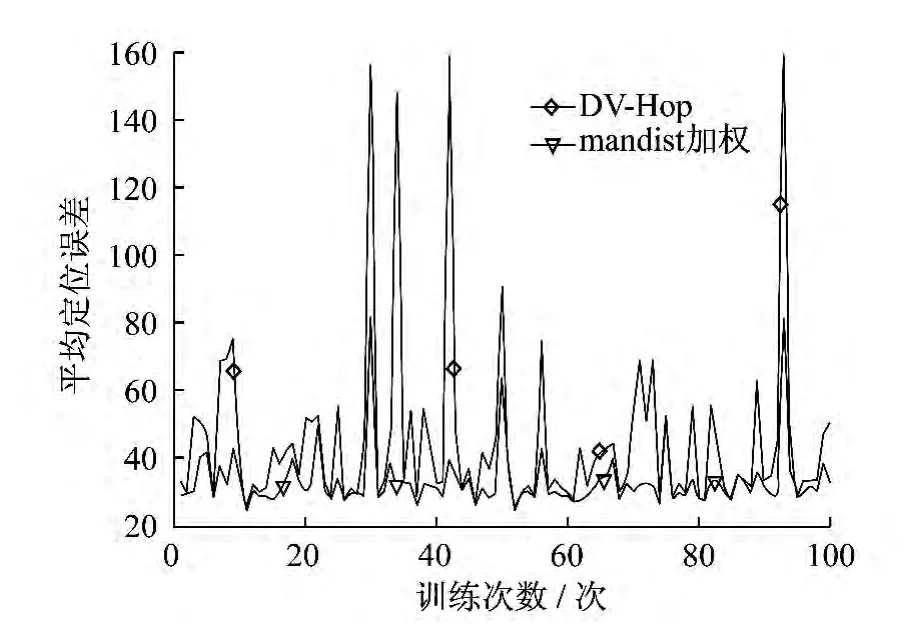
图4 mandist加权和DV-Hop算法每次定位误差对比

3种算法随训练次数增加的平均定位误差对比如图5所示.

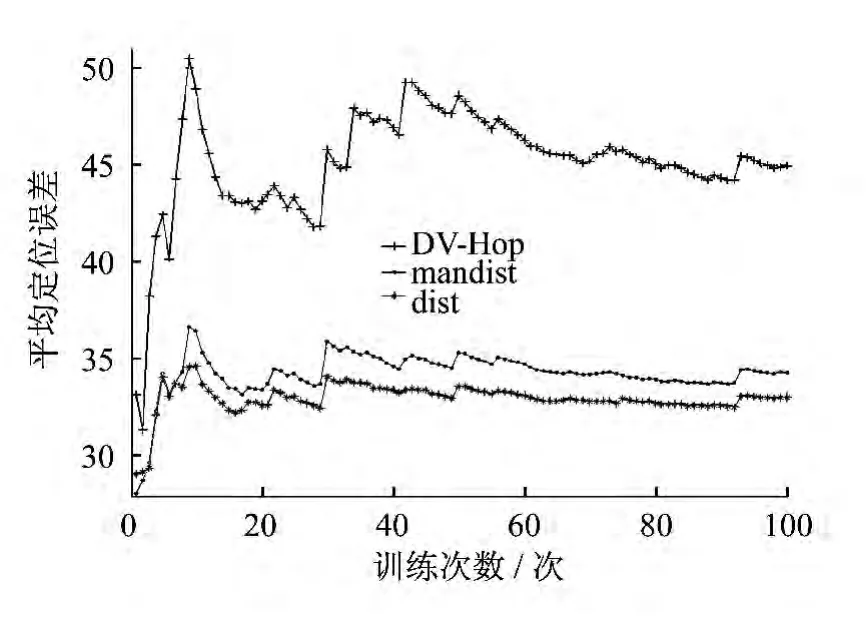
图5 3种算法随训练次数增加的平均定位误差对比

当仿真训练次数变化到10次时，与DV-Hop算法相比，两种加权改进方法的平均定位误差变化幅度较小，而DV-Hop算法则较大.相比DV-Hop算法，经过mandist加权的最小二乘法的平均定位误差降低了21.48%;dist加权的最小二乘法降低了22.49%.从10～100次，DV-Hop算法平均定位误差变化幅度比较大，且在29～50次中呈现出增加趋势;mandist加权的最小二乘法的平均定位误差从30 次开始保持在33.751 4 ～35.655 0，变化幅度比较小，比较稳定;dist加权的最小二乘法的平均定位误差从30次开始保持在32.589 2～33.976 9，变化幅度也较小，而且误差有降低的趋势，最后基本保持不变，也比较稳定.

3.2 锚节点数变化分析

随着锚节点数增加而变化的3种定位算法的平均定位误差对比如图6所示.

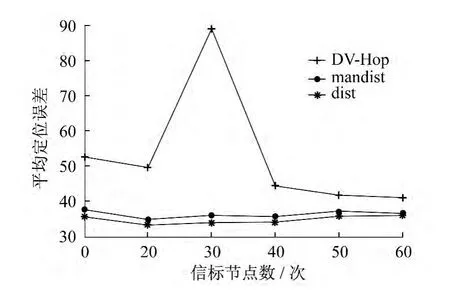
图6 随锚节点增加时3种算法的平均定位误差对比

由图6可以看出，随着信标节点的增加，DVHop算法平均定位误差波动较大，并且误差也较大，平均误差为52.233 2;经过 mandist加权的最小二乘法算法，误差波动很小，平均误差为36.180 9，比 DV-Hop 算法降低了 30.73%，且较为稳定;经过dist加权的最小二乘法，误差波动也较小，平均误差为34.754 4，比 DV-Hop算法降低了33.46%，很稳定，并且误差最小.由此可以看出，由mandist和 dist加权改进的 DV-Hop算法，两者都非常稳定，但dist加权算法更为理想.

4 结语

本文提出了两种改进DV-Hop定位算法，即mandist加权最小二乘法和dist加权最小二乘法.这两种算法对经典DV-Hop算法存在误差较大的平均跳距进行了最小跳数mandist和dist加权处理，使得改进后的DV-Hop算法能更加有效地对平均每跳距离进行估计.由仿真结果可以看出，与经典的DV-Hop算法相比，本文提出的两种改进算法的平均定位误差有所降低，而且定位精度更为稳定.

[1]许秀兰.无线传感器网络距离无关定位算法研究[J].计算机与现代化，2009，4(10):6-9.

[2]张松涛，蒋洪波，唐振华，等.无线传感器网络中一种精细距离控制定位算法[J].计算机科学，2010(4):80-83.

[3]谢晓松，程良伦.传感器网络基于移动信标改进的DV-Hop定位算法[J].计算机应用与软件，2011(4):33-36.

[4]李冰，李聪.基于移动代理的无线传感器网络节点定位算法[J].计算机时代，2010(10):10-13.

[5]方海涛，雷菁，胡昆明，等.基于 RSSI修正的改进 DV-Hop测距算法[J].通信技术，2012，45(2):16-18.

[6]王建刚，王福豹，段渭军.加权最小二乘估计在无线传感器网络定位中的应用[J].计算机应用研究，2006(9):41-43.

[7]梁银.传感器网络中的数据查询处理[J].计算机应用与软件，2008，25(5):201-202.

[8]杨军.无线传感网络节点定位算法综述[J].仪器仪表标准化与计量，2012(1):38-41.