基于交叉导纳矩阵的单相桥式整流性负荷的谐波建模

林顺富，叶建荣，赵伦加

(上海电力学院 电气工程学院，上海 200090)

近年来，随着国家经济的发展和居民生活的持续改善，以及社会对节能和环境保护意识的提高，越来越多的电力电子型非线性负荷在居民家庭中得到了应用，电力系统谐波产生来源正在逐渐发生变化.

基于电力电子的现代负荷越来越广泛应用于居民家庭中，在配电网中产生越来越多的谐波.例如，大量高能效荧光灯替代了传统的白炽灯，液晶电视机代替了彩色、黑白电视机等.这些谐波源具有类似的大小并分布在整个电力网络中，成为目前日益突出和引起极大关注的新型谐波源——分布式谐波源.

居民家庭中的单相桥式供电负荷包括台式电脑、笔记本电脑、液晶电视机、冰箱等.测试表明，液晶电视机输入电流总谐波含量高达137%，3次、5次、7次谐波畸变率分别高达 90%，75%，70%.由于较高次的谐波(特别是高次谐波)会沿着输电线路产生传导干扰和辐射干扰，进而对供电系统产生污染，影响其他用电设备的安全经济运行.因此，对居民家庭非线性负荷的谐波模型的研究非常必要.

居民负荷的谐波模型通常采用固定幅值的谐波电流源表示，所建立的模型简单方便，但模型没有考虑系统不平衡、变负载、谐波电压畸变等非典型运行情况，降低了模型的精度和使用范围.[1-2]文献[3]至文献[5]采用通用负荷模型，通过参数辨识对负荷进行建模，同样不能反映输入电压畸变时的情况.

考虑到大量非线性负荷接入电网时供电电压含有畸变的情况，本文针对居民家庭中的单相桥式供电负荷，建立了其频域谐波交叉导纳矩阵模型，[6-9]分析了其特性，并利用仿真和实验验证了该模型的准确性.

1 谐波分析电路

居民家庭中单相桥式供电负荷产生的谐波主要来源于开关电源，其原因主要有以下两个方面:一是由开关电源中普遍采用的电容滤波型桥式整流电路造成输入电流波形畸变引起的;二是由电源电路中的开关器件(二极管、三极管)及感性负载工作于15 kHz左右的高频开关状态产生尖峰脉冲引起的.相对于整流电路产生的谐波含量，由开关器件引起的谐波含量较小，本文只研究由整流电路造成的电流畸变.居民家庭中单相桥式供电负荷的谐波分析电路[10-14]如图1所示.其中，L为输入滤波电感;C为大容量直流滤波电容;R为负载等效电阻;uac为输入端电压;udc为含纹波的直流输出电压.

该电路电容有充、放电两种工作状态.仅当交流侧输入电压uac的绝对值大于直流侧电压udc时，二极管桥导通，滤波电容处于充电阶段，交流侧流过电流iac;其余时刻二极管桥关断，滤波电容对R放电.电容充电时间只占交流半周期中的很小部分，因此交流电流呈间断的脉冲状波形，含有丰富的谐波.

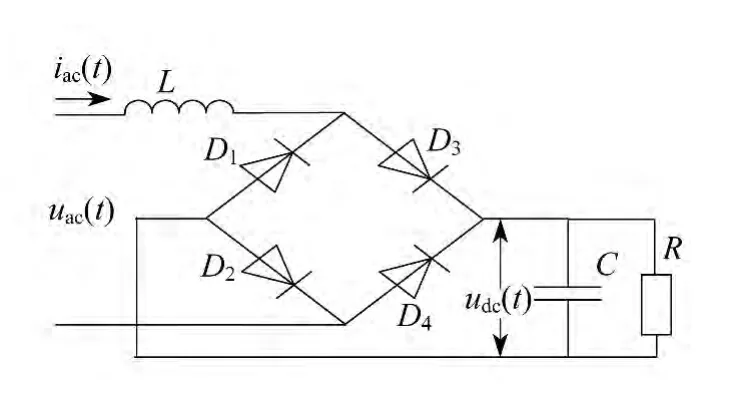
图1 单相桥式谐波分析等效电路

用一个可变电阻Rd来模拟二极管单相桥，如图2所示.当二极管单相桥导通时，Rd=Ron;当二极管单相桥关断时，Rd=Roff.另外，为了简化公式及计算，可以忽略二极管的电压降.

图2 单相桥式供电负荷的谐波分析简化电路

图2 的状态空间方程描述如下:

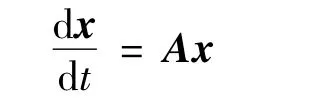
即

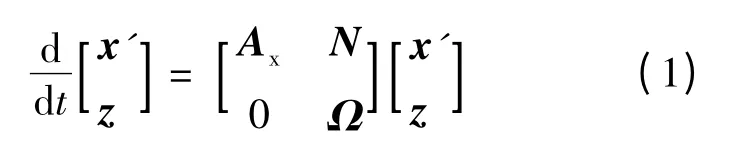
其中

(1)二极管单相桥导通和关断时Rd取值不同，所以状态转移矩阵A是时变矩阵.为了区别Rd=Ron和Rd=Roff两种不同的情况，A分别用Aon和 Aoff表示.

(2)在实际系统中，电源电压不是理想的基波电压，而是包含若干奇数次谐波.设电源电压为:

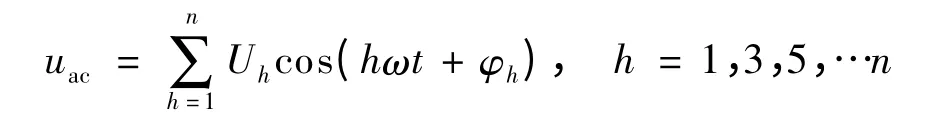
(3)uxh和uyh表示一对h次谐波电压:

图3为在连续导通的情况下，交流侧电压波形、电流波形及直流侧电压波形图.图3中，α表示交流电压和直流侧电压之差为零的时刻，对应着二极管桥的导通角;而(α+μ)表示交流侧电流为零的时刻，对应着二极管桥的截止角.

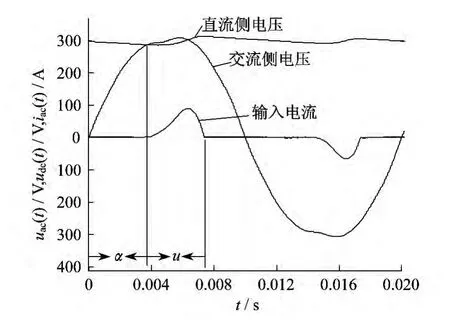
图3 输入侧电压、直流侧电压及电流波形

为了明确描述谐波等效电路的工作过程，必须想办法解出α和μ.分别分析二极管桥导通和截止时的情况.

当二极管导通时，则有:

当二极管关断时，则有:

式中:C1=[1 0 0…0].

为了求解方程(2)和方程(3)，必须找到另一个关于udc(α)和α的方程表达式.在导通的稳态过程中可以得到式(4);又因为在后半周期，交流侧电压、电流与前半周期大小相等符号相反，直流侧电压保持不变，可以得到式(5).

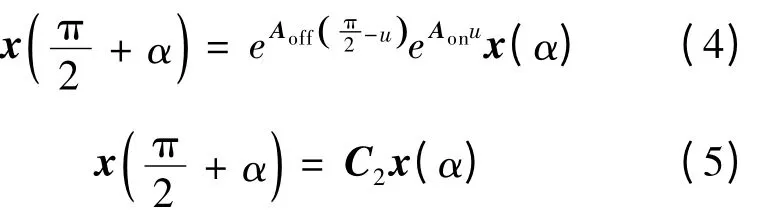
式中:C2=[－1 1 －1… －1].

联合式(4)和式(5)可以得到:

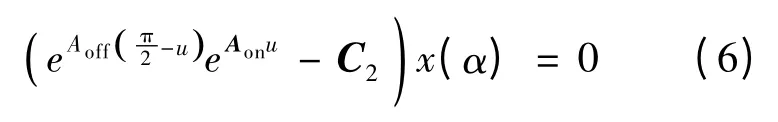
令

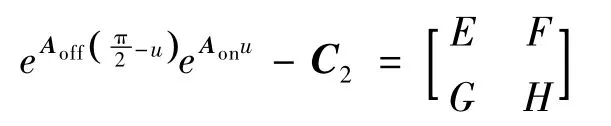
则

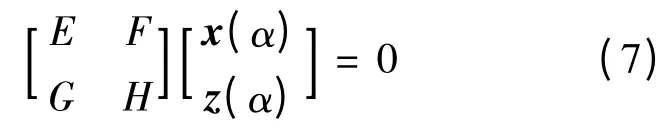
展开得到:

由式(8)可以得到一个关于udc(α)和α的方程表达式.由于式(2)、式(3)、式(8)都是超越方程，故可以采用牛顿数值迭代方法进行求解，求解过程如图4所示.

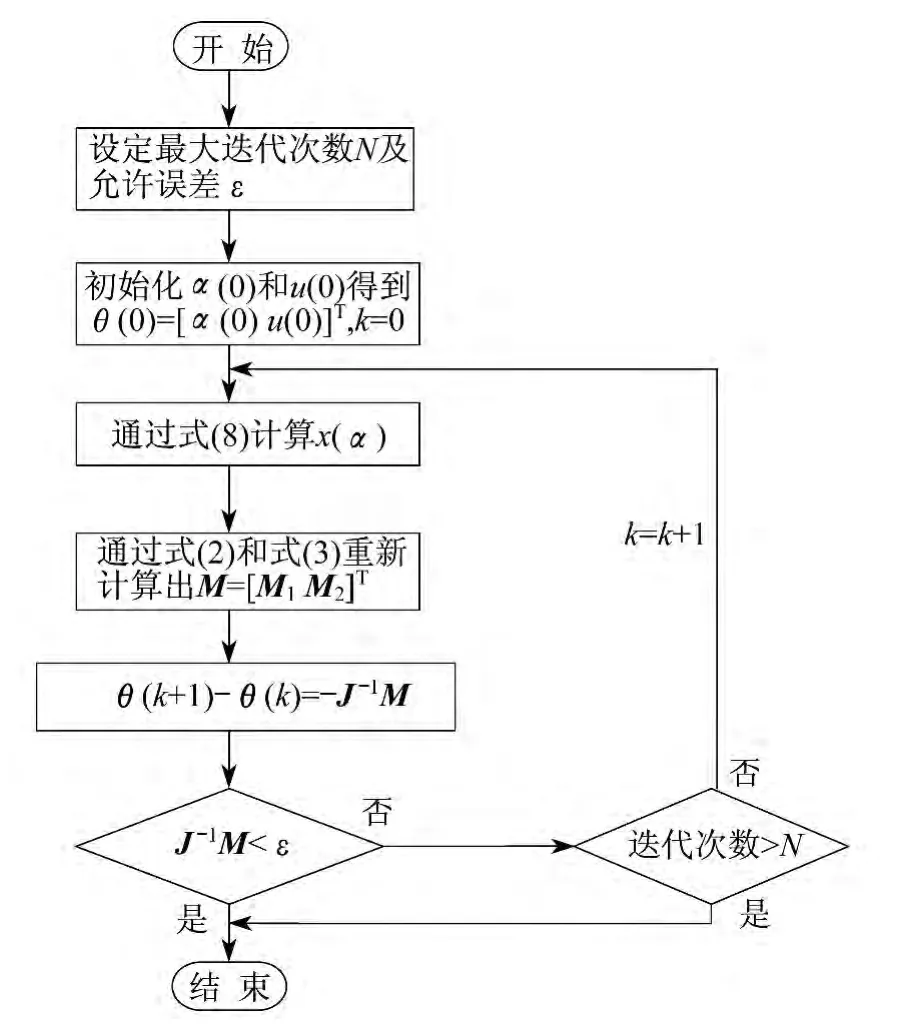
图4 数值迭代流程

图4 中:

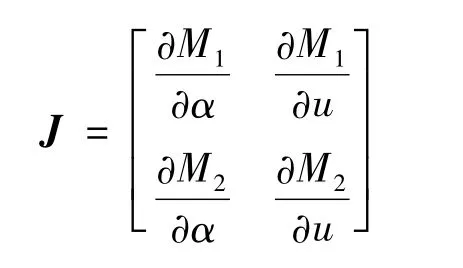
运用上述迭代方法，以液晶电视机为例，求解得到两种不同供电电压情况下谐波分析等效电路的参数，如表1所示.

表1 案例1和案例2的求解结果

2 基于交叉导纳矩阵的谐波模型

2.1 谐波交叉导纳矩阵的推导

一般来说，大部分的频域算法可以表达为:

式中:U——含谐波的交流输入端电压向量;

I——谐波电流向量;

Y——谐波导纳矩阵.

为了得到导纳矩阵，由式(1)展开可得到如下方程:

为了简化计算，忽略二极管两端压降.假设直流侧电压保持不变，取Udc=udc(α).对方程两边同时积分，通过欧拉公式换算得到iac(t).为了解出电流的各次谐波含量，将iac(t)在一个周期里做傅里叶变换，则有:

将式(11)得到的结果整理成矩阵的形式，就可以得到液晶电视机交叉导纳矩阵模型:

即:

式中:

矩阵Y+反应了交流侧输入端各次谐波电压对各次谐波电流的影响大小;Y－反应了交流侧输入端各次谐波电压的共轭对各次谐波电流的影响大小;Yk，h表示第h次输入谐波电压对第k次谐波电流所产生的影响大小.

方程(12)是单相整流电路的谐波耦合矩阵模型.可以看出，该方程的推导来源于电器基本电路的结构，几乎没有近似之处.因此，对非线性的单相桥式整流电路来说，该模型是一个精确的频域表达式.它将非线性特性有效地转化为一个线性的模型.另外，与普通线性化的模型相比，该频域模型具有以下两个特点:一是它耦合了所有次谐波电压和各次谐波电流分量，各次谐波电压都对每次谐波电流的产生有一定的影响;二是交流侧电流不仅是关于交流侧端电压的函数，它也与供电侧电压的共轭相量电压有关.然而与诺顿等效模型相比，导纳矩阵模型最重要的特征是具有相对于供电侧电压的恒定性，即矩阵的元素与供电侧各次谐波电压是相互独立的，不随之改变.这意味着该模型在频域中是一种线性表达式，且由于其线性特性，不管供电电压是否含有谐波，都可以提前计算出导纳矩阵的各个元素.

2.2 谐波交叉导纳矩阵的特性分析

为了更好地分析谐波交叉导纳矩阵及模型的特性，[15]采取上述案例1以液晶电视机为例对模型进行求解.为方便比较，将Y+，Y－，Y0几个元素都以其各自的最大元素为基准进行换算，求解出的矩阵的各元素模值大小对比如图5，图6，图7所示.

图5 Y+矩阵元素幅值大小对比示意

图6 Y－矩阵元素幅值大小对比示意

由图5，图6，图7可以总结出Y矩阵元素有如下特性:矩阵是满秩矩阵，矩阵元素的模值随谐波次数的增加而递减，说明高次谐波电压的影响较小;3个矩阵在各自矩阵中的模值最大，说明基波电压对基波电流影响最大;Y+和Y－矩阵的第一行元素的模值相对较大，说明基波电流受各次谐波电压影响较大，但由于谐波电压值较小，其影响效果不一定显著;Y+和Y－矩阵的第一列元素的模值相对较大，说明各次谐波电流受基波电压影响较大，且由于基波电压值大，影响效果十分显著;Y+和Y－矩阵对角线元素相对较大，说明h次谐波电压对h次谐波电流影响较大，但由于谐波电压值相对较小，其影响效果不一定显著;除第一行、第一列及对角线元素相对较大外，其他耦合元素较小，说明各次谐波的耦合特性不是特别明显.由此可以看出，所提出的频域谐波交叉导纳矩阵模型耦合了所有次谐波电压和各次谐波电流分量，能够反映各次谐波电压对每次谐波电流产生的影响.

图7 Y0矩阵元素幅值大小对比示意

3 仿真与实验验证

为了验证交叉导纳矩阵模型的正确性，本文对模型推导结果、实验采集的数据以及Matlab仿真结果进行了对比.其中，实验室液晶电视机输入端交流电压情况如表2所示;谐波等效电路的各项参数取值如表3所示.图8为案例1的交流侧电流谐波频谱对比;图9为案例2的交流侧电流波形对比.

由图8和图9可以看出，通过谐波导纳矩阵模型计算的各次谐波电流幅值与实测和仿真所得的结果都十分近似;导纳模型计算的各次谐波电流相角与实测和仿真所得的结果相比，较低次谐波的相位十分接近，但部分高次谐波相位上有显著的差异，可能是由文中谐波分析等效电路与实际单相桥式整流负荷的开关电源电路谐波产生特性的细微差异引起的.此外，由于实际测量中谐波相位信息对实验室测量环境要求较高，对测量误差十分敏感，也容易引起模型计算结果与实际测量结果之间的差异.

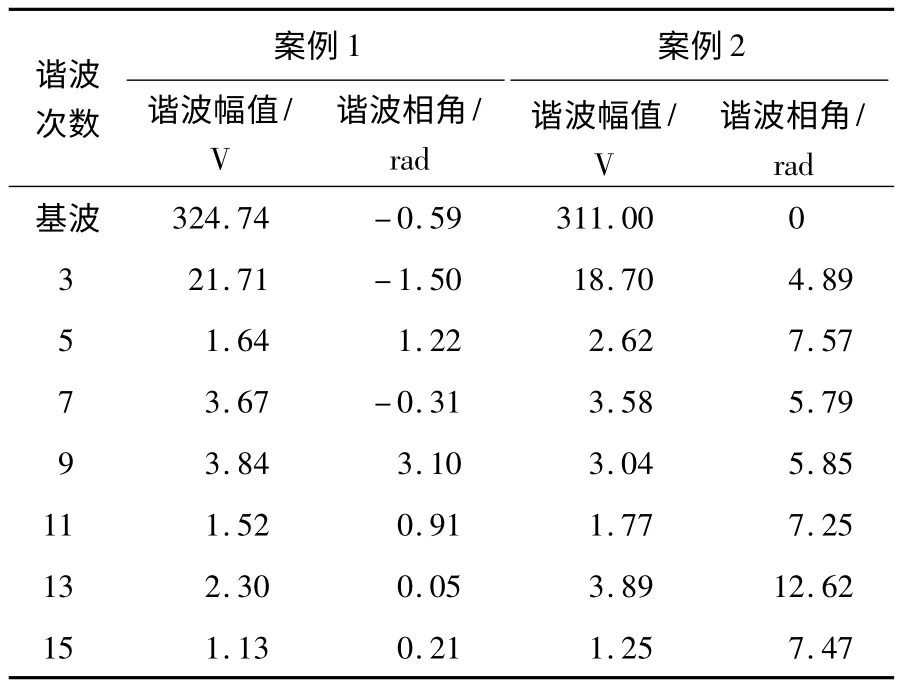
表2 输入端交流电压情况

表3 谐波等效电路各项参数值

图8 案例1交流侧电流谐波频谱对比

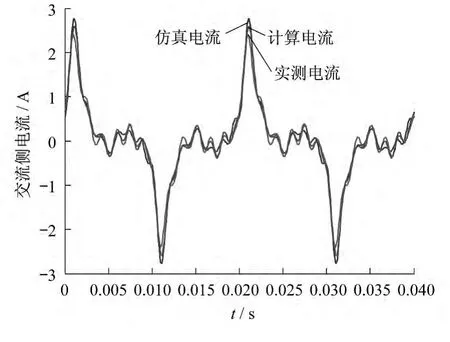
图9 案例2交流侧电流波形对比

4 结语

基于居民家庭中的单相桥式供电负荷开关电源的基本电路，以液晶电视机为例，建立了其频域谐波交叉导纳矩阵模型.通过数值迭代计算得到电路参数，进而对比模型计算结果和仿真及实测结果，验证了交叉导纳矩阵在谐波计算上的较高准确性.而且在交叉频率导纳矩阵模型中考虑到了各次谐波电压对各次谐波电流的影响，克服了传统恒谐波电流源模型不能反映供电电压畸变时存在的谐波衰减效应的缺陷，同时也克服了Norton等效模型参数受供电侧电压波动影响的缺点.由于模型的推导是基于居民家庭中的单相桥式供电负荷的基本电路，因此该模型可推广到其他具有类似电源电路结构的装置.

[1]王奎，李建超，潘贞存，等.居民用户谐波调查及仿真分析[J].电力系统保护与控制，2008，36(22):88-92.

[2]郑连清，吴萍，李鹍.电力系统中谐波源的建模方法[J].电网技术，2010，34(8):41-45.

[3]吴笃贵，徐政.电力负荷的谐波建模[J].电网技术，2004，28(3):20-24.

[4]冯士刚，艾芊，徐伟华，等.基于瞬时对称分量的负荷谐波建模[J].高电压技术，2008，34(4):783-787.

[5]冯士刚，艾芊.一种谐波负荷建模的新方法[J].电力系统自动化，2007，31(17):26-30.

[6]FAURI M.Harmonic modelling of non-linear load by means of crossed frequency admittance matrix[J].IEEE Transactions on Power Systems，1997，12(4):1 632-1 638.

[7]SUN Y，ZHANG G，XU W，et al.A harmonically coupled admittance matrix model for AC/DC converters [J].IEEE Transactions on Power Systems，2007，22(4):1 574-1 582.

[8]雍静，陈亮，陈双燕.台式计算机负荷的频域谐波模型及衰减特性[J].电机工程学报，2010，30(25):122-129.

[9]MANSOOR A，GRADY W M，THALLAM R S，et al.Effect of supply voltage harmonics on the input current of singlephase diode bridge rectifier loads[J].IEEE Transaction on Power Delivery，1995，10(3):1 416-1 422.

[10]El-SAADANY E F，SALAMA M M A.Effect of interactions between voltage and current harmonics on the net harmonic current produced by single-phase non-linear loads[J].Electric Power Systems Research，1997，40(3):155-160.

[11]PETER W Lehn. Direct harmonic analysis of the voltage source converter[J].IEEE Transactions on Power Delivery，2003，18(3):1 034-1 042.

[12]LEHN P W，LIAN K L.Frequency coupling matrix of a voltage-source converter derived from piecewise linear differential equations[J].IEEE Transactions on Power Delivery，2007，22(3):1 603-1 612.

[13]LIAN K L，LEHN P W.Harmonic analysis of single-phase full bridge rectifiers based on fast time domain method[C].IEEE International Symposium on Industrial Electronics，2006(4):2 608-2 613.

[14]CARPINELLI G，LACOVONE F，VARILON P，et al.Single phase voltage source converters:analytical modeling for harmonic analysis in continuous and discontinuous current conditions[C].International Journal of Power and Energy Systems，2003，23(1):37-48.

[15]JING Yong，LIANG Chen，ALEXANDRE B Nassif，et al.A frequency-domain harmonic model for compact fluorescent lamps[J]. IEEE Transaction on Power Delivery，2010，25(2):1 182-1 189.