基于自适应量子遗传算法的电力系统机组组合问题

于艾清，刘 滔

(上海电力学院 电气工程学院，上海 200090)

节能减排发电调度[1]要求在电力系统安全稳定运行和连续供电的前提下，最大限度地减少能源和资源的消耗，以及污染物的排放.其中，机组组合优化是编制短期发电计划首先要解决的问题，是整个发电计划的基础.火电机组组合调度问题(Unit Commitment Problem，UCP)是指在满足大量运行约束下在某一特定时间内安排机组运行状态来满足预测的负荷需求，使其达到某些目标.[2]

由于UCP的非确定多项式(NP)的难特性及其经济重要性，一直以来都是电力生产企业的重点关注问题.传统的确定性算法有优先权(PL)方法、动态规划(DP)、混合整数规划、分支定界算法和拉格朗日松弛法，利用这些方法在求解过程中或多或少都存在一些缺点，得不到十分理想的结果.[3]

现代的智能优化方法如遗传算法、人工神经网络、粒子群算法、蚁群算法和量子进化算法[4-9]等，为解决 UCP问题提供了较好的方法，因此得到了广泛应用.其中，量子遗传算法(Quantum Genetic Algorthm，QGA)结合了量子计算和遗传算法的优点，得到了较多学者的关注和研究.

但这些文献有很多相似之处，一是采用二进制编码方式，用0-1表示发电机组的运行状态，将所有机组的运行状态编码串接起来作为种群中的一个个体，编码规模大，影响算法效率;二是量子旋转角根据表格查询，根据问题不同有所区别，没有规则可循.

本文研究的火力发电机组组合问题以最小标准煤耗为优化目标，考虑机组自身约束和基本系统约束，提出了自适应量子遗传算法(Adaptive Quantum Genetic Algorithm，AQGA)求解该模型.对个体进行量子编码，缩短编码长度;采用量子旋转门作为遗传的进化操作，定义了针对个体适应值和进化代数的自适应量子旋转角，使个体向更好的解靠近;采用改进的随机窗口变异操作.最后，在仿真实验中改变各参数，分析和总结了其对算法求解机组组合问题性能的影响，并验证了算法的有效性.

1 机组组合问题的数学模型

本文研究的机组组合优化问题就是在一定的约束条件下求得目标函数的极小值，这是一个有整数变量、连续变量及非线性函数的混合整数非线性规划问题.

1.1 目标函数

要求系统在T小时时段内各机组的总发电成本为最小.总发电成本包括发电机组运行耗能成本和启动耗能成本(煤耗成本).目标函数可写为:

式中:T——机组调度总周期，将其分为T个时段;

N——机组或等效机组台数;

U it——机组i在t时段运行状态变量，U it=0表示运行;

Pit——机组i在t时段的功率变量，MW;

Fi(Pit)——机组i的运行耗能，t/h;

Si——机组i的启动耗量，它与停机时间的长短有关，t/h.

式(1)中发电机组的燃料费用采用二次函数形式表示为:

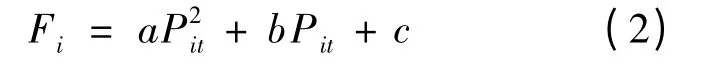
式中:a——发电机组i成本函数中二次项，t/WM2h;

b——发电机组i成本函数中一次项，t/MWh;

c——发电机组i成本函数中常数项系数，t/h.

1.2 约束条件

(1)功率平衡约束条件为:

式中:PDt——t时刻系统中的总负荷，MW.

式(3)表示任何时段电力负荷之和必须等于发电机发电出力之和.

(2)机组容量约束条件为:

式中:Pimin——机组i发电能力下限;

Pimax——机组i发电能力上限.

(3)机组启停次数约束条件为:

式中:M——机组启停的次数，机组不能频繁的启停.

(4)机组最小连续停运和连续运行小时数约束条件为:

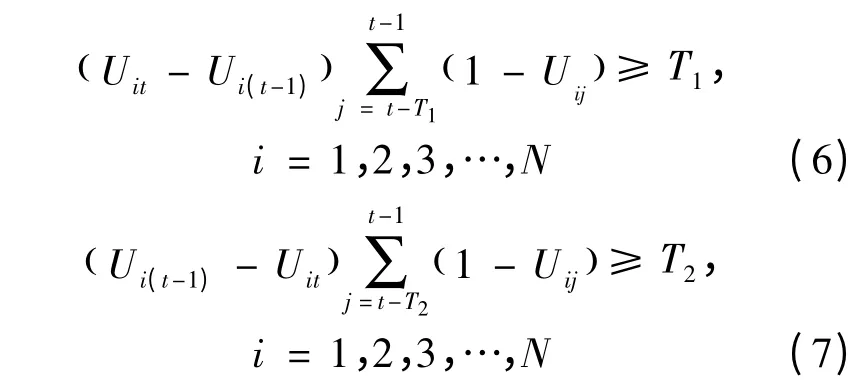
式中:T1，T2——每台机组的最小连续停运和连续运行小时数.

2 求解UCP的自适应量子遗传算法

量子遗传算法(QGA)是一种概率进化算法，是量子计算与进化计算理论相结合的新兴交叉产物.它使用量子位编码染色体这一概率幅值表示，可以使一个量子染色体同时表达多个状态的信息，用量子门对叠加态的作用作为进化操作，能很好地保持种群的多样性，避免选择压力问题，使得种群以大概率向着优良模式进化，从而实现目标的优化求解.

2.1 UCP的量子编码

本文提出了新的量子编码方式，在编码中考虑两个约束，即机组启停次数约束，机组最小连续停运和连续运行小时数约束.一个量子个体由N行5M+1列的矩阵构成.矩阵中每一行代表一个机组在24 h内的启停状态.每一行的第一列为机组的初始状态(0表示停止;1表示启动)，后面每5列代表一个启停位置的二进制码.矩阵中每一个二进制码都采用量子位表示:

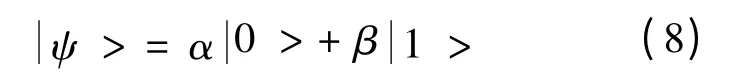
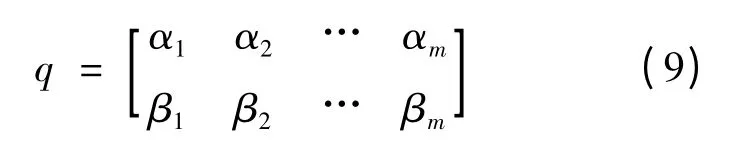
由此可以看出，一个具有m个量子位的个体可以表示2m个状态.这样，种群的多样性得到了丰富，更加有利于算法在搜索空间中搜索.

2.2 种群初始化

本文在初始化过程中，即对生成的矩阵进行约束处理.约束处理的先后顺序为:机组启停次数;机组最小连续停运和连续运行小时数;机组容量约束;功率平衡约束.

以某一台机组的启停位置生成为例，具体方法如图1所示.

图1 机组启停位置编码生成范例

2.3 自适应量子旋转操作

本文采用量子旋转门作为AQGA的主要进化操作，根据一般情况，量子门必须为可逆的酉矩阵.每个量子位都通过如下的量子旋转门来更新:

更新后的量子位如下:

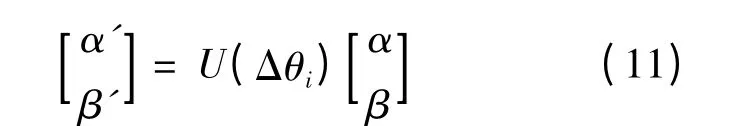
在量子旋转中，旋转角的选择对算法尤为重要，其幅度选择会影响算法的收敛速度，若幅度过大，会导致算法跨越的步长过大，从而会使算法陷入早熟;反之，又会使算法进行大量的冗余计算，导致算法的收敛速度变慢.

针对本文的最小总成本的机组组合优化模型，定义了自适应旋转角θi:

式中:θmin——最小旋转角;

θmax——最大旋转角;

fi——第i个体的适应值;

fmin——最小适应值;

fmax——最大适应值;

G——当前代数;

Gmax——最大代数.

式(12)表示个体较为优秀时，对旋转角进行较小的调整;个体较差时，使用相对较大的旋转角.在算法运行初期，设置较大的角步长大范围搜索最优解，后期则采用较小的角步长局部搜索最优解，从而在保证搜索效率的同时，兼顾了搜索精度.

2.4 变异操作

文献[10]针对实数编码的机组组合问题，提出了多窗口变异操作，但其窗口宽度w是一固定值，本文改进其窗口变异操作，宽度w随机确定.具体操作如下.

步骤1 将整数编码转换成二进制编码，并且根据二进制编码来确定机组出力矩阵，以此实数矩阵进行变异操作，变异前个体为:

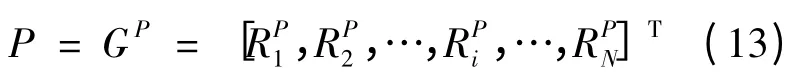
进行变异操作个体中的任意行向量R表示为:

式中:C i，t——编码矩阵中的第i行、第t列元素，表示发电机组i在时段t中的发电量大小.

变异后的个体为:

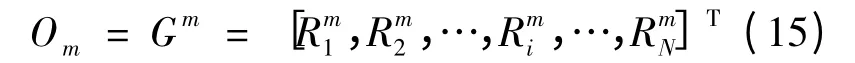
步骤2 生成随机数 α，α∈(0，1);确定窗口变异的起始位子j，满足j+w-1≤T;确定变异前的行向量

步骤3 进行窗口变异操作，生成变异个体O m.

具体方法如下:

2.5 算法流程

AQGA的算法流程如图2所示.

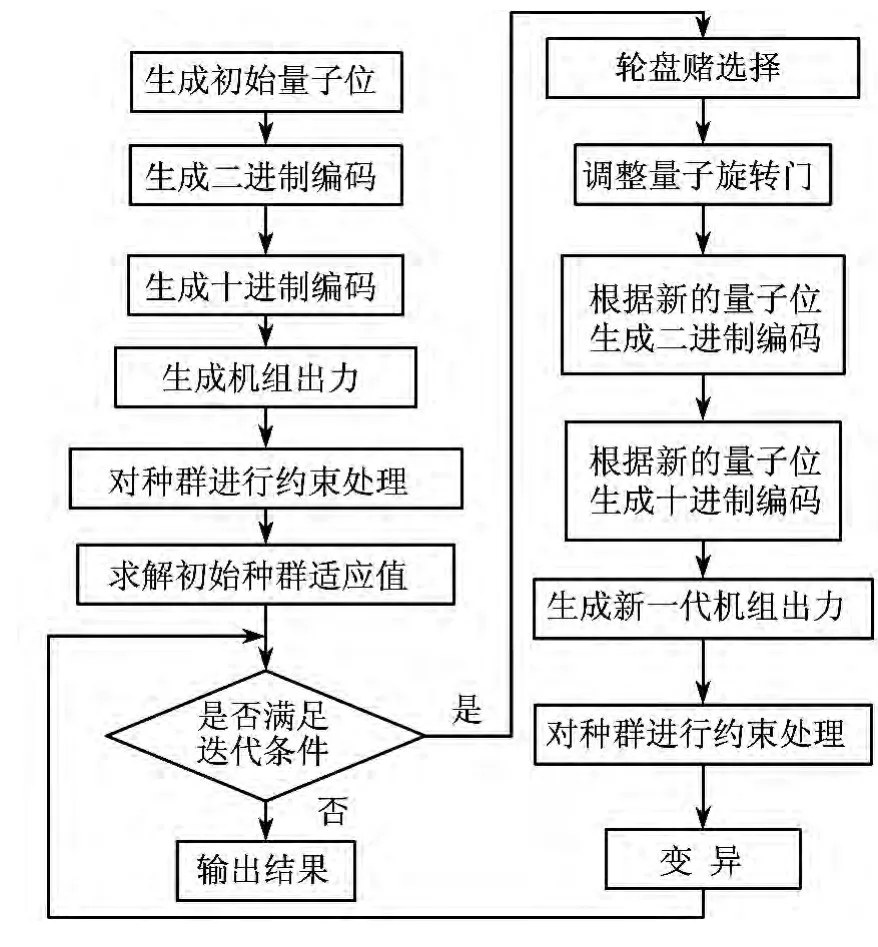
图2 AQGA算法流程

3 仿真算例分析

为验证本文中AQGA算法的有效性，采用文献[11]中的机组组合模型进行仿真研究.此次仿真在Intel Core-i5 3337U 1.8 GHz处理器4 G内存的Aspire V5-472G上运行，软件环境为Matlab 7.6.0(R2008a).

算法中的参数确定规则为，在确定其他参数不变的情况下，只对其中一个参数进行调整，并进行10次运算.综合考虑所得10次运算结果的平均值、最优值及运算时间，确定最优参数.经过大量仿真，最优算法参数设置为:进化代数为1 000代;种群规模为100;量子进化率为75%;变异率为2%;量子旋转角范围 θmin=0.05π，θmax=0.1π;机组启停次数为2次时的仿真结果为最优.

仿真的最优值结果进化曲线与甘特图见图3.其中，图3a的线的变化代表最优值随着进化代数的变化趋势，图3b是机组启停调度图，图中黑色框代表机组运行，白色框代表停机.

经过10次运算之后，最低耗费值的最小值是79 036 t，其运算时间是 26.482 9 s，10 次运算的平均耗量为 79 133.5 t，平均计算时间 27.831 4 s.相比于文献[11]所求得的运行耗量(80 766 t)降低了1 730，表明该AQGA算法有很好的收敛性和有效性.最优值各机组出力见表1.

图3 最优值结果进化曲线与甘特图

表1 最优值各机组出力

4 结语

本文提出了一种使用量子编码的自适应量子遗传算法来求解电力系统机组组合问题.提出的量子编码，采用了二维量子矩阵代替传统的二进制矩阵对发电安排进行编码，有效减小了矩阵规模，简化了计算，提高了计算效率.采用量子旋转门代替了传统遗传算法的交叉操作.提出的自适应量子旋转角，可根据问题自适应变化旋转角度.通过算例仿真分析，验证了该算法在求解机组组合问题时的有效性.

[1]中华人民共和国中央人民政府门户网站.国务院办公厅关于转发发展改革委等部门节能发电调度办法(试行)的通知(国办发[2007]53 号)[EB/OL].[2007-08-07].http:∥ www.gov.cn/zwgk/2007 - 08/07/content_708486.htm.

[2]王锡凡.机组组合问题的优化方法综述[J].电力系统自动化，1999，23(4):51-56.

[3]PADHY N P.Unit commitment——a bibliographical survey[J].IEEE Trans on Power Systems，2004，19(2):1 196-1 205.

[4]蔡超豪，蔡元宇.机组优化组合的遗传算法[J].电网技术，1997，21(1):44-47.

[5]GIL E，BUSTOS J，RUDNICK H.Short-term hydrothermal generation scheduling model using a genetic algorithm[J].IEEE Trans.on Power Systems，2003，18(4):1 256-1 264.

[6]赵波，曹一家.电力系统机组组合问题的改进粒子群优化算法[J].电网技术，2004，28(21):6-10.

[7]SISHAJ P Simon，PADHY Narayana Prasad，ANAND R S.An ant colony system approach for unit commitment problem[J].International Journal of Electrical Power ＆ Energy Systems，2006，28(5):315-323.

[8]LAU T W，CHUNG C Y，WONG K P，et al.Quantuminspired evolutionary algorithm approach for unit commitment[J].IEEE Transactions on Power Systems，2009，24(3):1 503-1 512.

[9]于艾清，顾幸生.一种求解同等并行机调度的混合量子衍生进化算法[J].控制与决策，2011，26(10):1 473-1 478.

[10]孙力勇，张焰，蒋传文.基于矩阵实数编码遗传算法求解大规模机组组合问题[J].中国电机工程学报，2006，1(2):82-87.

[11]韩学山，柳焯.考虑发电机组输出功率速度限制的最优机组组合[J].电网技术，1994，18(6):11-16.