基于ATENA的钢筋混凝土无腹筋梁的非线性有限元分析*

易伟建，吴羽宇

(湖南大学 土木工程学院，湖南 长沙 410082)

基于ATENA的钢筋混凝土无腹筋梁的非线性有限元分析*

易伟建†，吴羽宇

(湖南大学 土木工程学院，湖南 长沙 410082)

通过ATENA软件建模对Bresler-Scordelis梁进行非线性有限元模拟，将模拟结果与试验结果进行对比，验证了所建立的有限元模型能较好地模拟无腹筋简支梁的破坏过程和破坏形态.采用已验证的有限元模型对Kani试验的133根梁进行了计算，模型能够准确地模拟试验梁的破坏荷载.通过对Kani梁计算结果的进一步分析发现，随剪跨比的增大，“拱”作用对梁受剪承载力的贡献逐渐减小，“齿”作用对梁受剪承载力的贡献逐渐增大.无腹筋简支梁名义极限剪应力随剪跨比的增大而减小，在剪跨比为2.5处，曲线发生明显转折，剪跨比小于2.5时减小幅度较大，剪跨比大于2.5后减小幅度较小.对于其他条件相同情况下的梁，在剪跨比超过2.5后，抗剪承载力减小幅度较小甚至基本保持不变，而剪跨区段的长度增大，导致破坏弯矩增大，破坏弯矩与截面计算最大受弯承载力的比值增大，因此，Kani提出的“剪切破坏谷”在剪跨比超过2.5后出现上升段.

无腹筋梁；名义极限剪应力；“拱-齿”模型；有限元分析；ATENA

自20世纪初至今，钢筋混凝土构件抗剪计算的理论和试验研究一直在不断地探索中，各国研究者们提出了大量的抗剪模型和理论.最早的桁架模型至今已有100余年.1964年，Kani[1-2]提出了“拱-齿”模型对无腹筋梁的工作机理及弯剪裂缝进行解释，认为无腹筋梁的剪力传递是通过“拱-齿”实现的，大剪跨比梁的受力以“齿”为主，而小剪跨比梁的受力则以“拱”为主.1980年，Hamadi和Regan[3]对齿模型进行了发展，假定裂缝方向是垂直的，且裂缝间距为梁截面有效高度的一半.1986年，Collins和Vecchio[4]在压力场理论的基础上考虑了开裂混凝土的拉应力作用，即修正压力场理论.1990年，Kotsovos[5]在试验研究的基础上提出了压力路径理论，认为压力的传递有一定的路径，与裂缝垂直的拉应力使该路径破坏，从而无法传递压力，导致梁发生剪切破坏.尽管抗剪理论研究起步较早，但由于剪切机理本身的复杂性，至今仍没有完善且受到公认的抗剪理论模型.

随着计算技术的进步，非线性有限元方法已逐渐成为钢筋混凝土结构分析和设计的一种非常有效的方法.1967年，Ngo和Scordelis[6]首次把有限单元法应用于钢筋混凝土简支梁的抗剪分析中，为钢筋混凝土有限元分析方法奠定了基础.几十年来在这一领域的大量研究[7-8]形成了丰富的成果，并集中反映在有限元分析的大型商业软件中，如ABAQUS，ANSYS等.利用非线性有限元分析软件，可以在计算模型中分别反映混凝土和钢筋材料的非线性特性，考虑或模拟钢筋与混凝土之间的粘结滑移，并在一定程度上模拟结点的构造和边界条件.软件后处理可以提供大量诸如应力、变形的全过程，结构开裂后的各种状态等结构反映信息.非线性有限元软件分析已经可以部分代替试验进行大量的参数分析，为合理的工程设计或规范修订提供依据.

ATENA软件是针对土木工程领域的一款非线性有限元分析软件.专注于混凝土结构的有限元分析，在混凝土开裂破坏和钢筋屈服方面有其独特的专业性.与其它软件相比，ATENA能够更加自由地定义材料性能，更加真实地模拟钢筋混凝土结构的行为，包括混凝土开裂、压碎和钢筋屈服等问题.该软件对混凝土结构的裂缝开展形态的模拟更是其它软件无法做到的.

本文利用ATENA软件建立有限元分析模型，先对Bresler-Scordelis的试验梁进行模拟分析，说明模型的适用性.而后对Kani的无腹筋梁受剪试验进行有限元模拟，将模拟结果与试验结果进行对比，并绘制“剪切破坏谷”.最后，以有限元数值模拟结果为基础，揭示“拱”作用以及“齿”作用对梁承载力的贡献随剪跨比增大而变化的情况，并进一步解释Kani提出的“剪切破坏谷”.

1 ATENA模型验证

1.1 试验简介

1963年，美国加州伯克利分校的Bresler和Scordelis两位教授在ACI发表了一篇钢筋混凝土简支梁抗剪性能试验研究的论文[9]，试验数据的可靠性得到公认使之成为所谓的Benchmark试验而被计算分析广泛引用进行模型校核.2004年，加拿大多伦多大学的Vecchion教授重复了Bresler和Scordelis的试验[10]，证明当年的试验观测结果是可以重现的.因此，可以采用Bresler和Scordelis的试验结果对有限元分析模型进行校核.由于Kani试验缺少梁剪切破坏时的极限挠度数据，也需要另外选择试验结果对ATENA有限元模型进行验证.

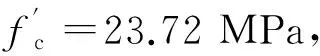
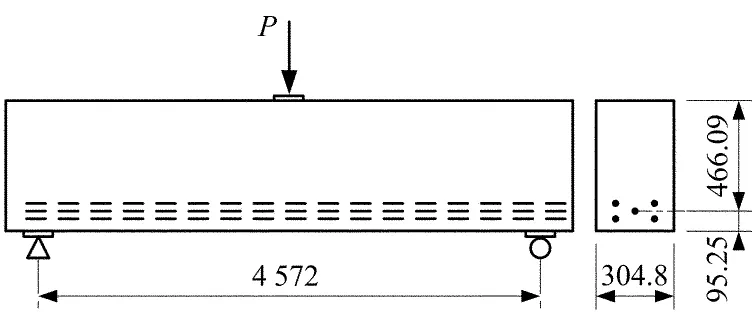
图1 试验梁截面尺寸及荷载布置(单位：mm)

1.2 模型建立及相关材料参数取值

ATENA为不同的研究目的研究对象提供了丰富的材料模型[11].

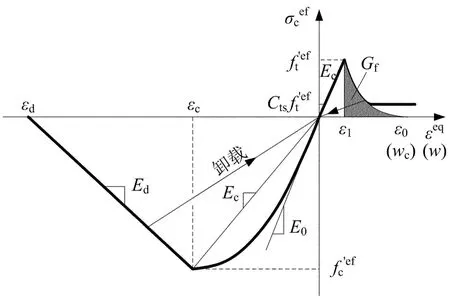
图2 混凝土等效单轴应力-应变关系[11]

对图2所示曲线作如下说明：

图3 混凝土双轴失效曲线[11]

对图3所示曲线作如下说明：

ATENA使用弥散裂缝模型，假定裂缝均匀地分布在单元内部而不是发生在单元之间.将混凝土材料处理为各向异性材料，利用混凝土的材料本构模型来模拟裂缝的影响[14].裂缝模型分为定角裂缝模型和转角裂缝模型.ATENA通过设置定角裂缝系数来对上述两种模型进行选择，根据大量的数值模拟算例可知定角裂缝模型的计算结果更接近实际结果.因此，将定角裂缝模型系数设置为1.0.

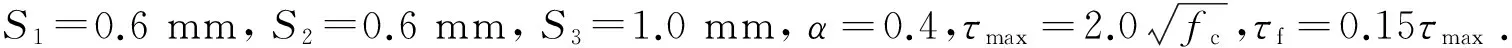
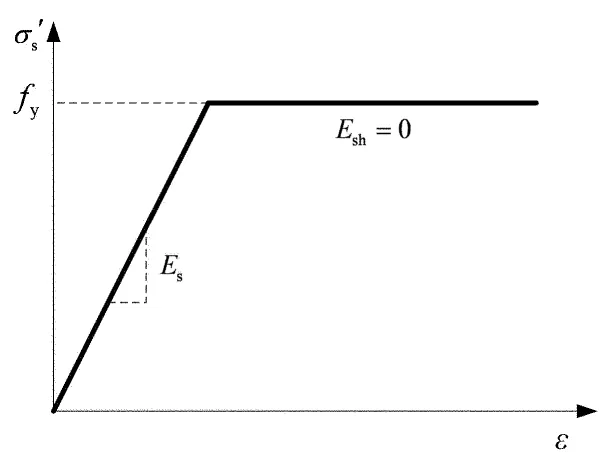
图4 钢筋应力-应变曲线

图5 CEB-FIB Model Code 1990粘结滑移准则

试验中，为了防止加载面及支座处发生局部受压破坏，在梁加载处和支座处设置钢垫板，以增加接触面积和刚度.因此，模拟梁也在加载处与支座处设置尺寸为304.8 mm×100 mm×20 mm的钢垫板.另外，本文分析没有考虑材料的随机性，忽略滚轴支座和铰支座导致的轴向变形的微小不对称，可采用对称1/2模型，即支座处约束竖向及梁宽方向位移，跨中截面约束梁长度方向的位移.为了便于收敛，模拟采用位移控制加载.

混凝土单元类型为六面体单元，钢筋为杆单元，支座及加载点钢垫块为四面体单元.垫块与混凝土单元之间不考虑单元兼容.兼顾计算准确性和计算速度，单元尺寸取为0.05 m.

1.3 Bresler-Scordelis试验梁模拟结果

分析得到荷载-挠度曲线和裂缝开展情况与试验结果的比较如图6和图7所示.从图6可以看出，荷载-挠度曲线得到较好的模拟，破坏荷载的模拟误差仅为1.25%.通过对图7的观察，发现裂缝开展和破坏形态也得到较好的模拟.应当指出，由于混凝土结构本质的随机性以及裂缝界面的复杂性，目前的有限元分析难以捕捉钢筋混凝土梁受剪破坏过程中的局部性能，但可以认为本文建立的有限元模型可以较精确地描述梁的受力过程，并以此为基础进行相应的应力分析.

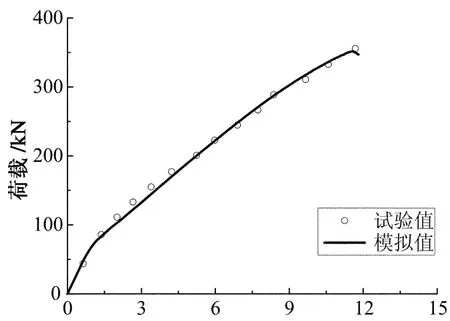
位移/mm

2 Kani试验梁的有限元模拟

2.1 试验简介

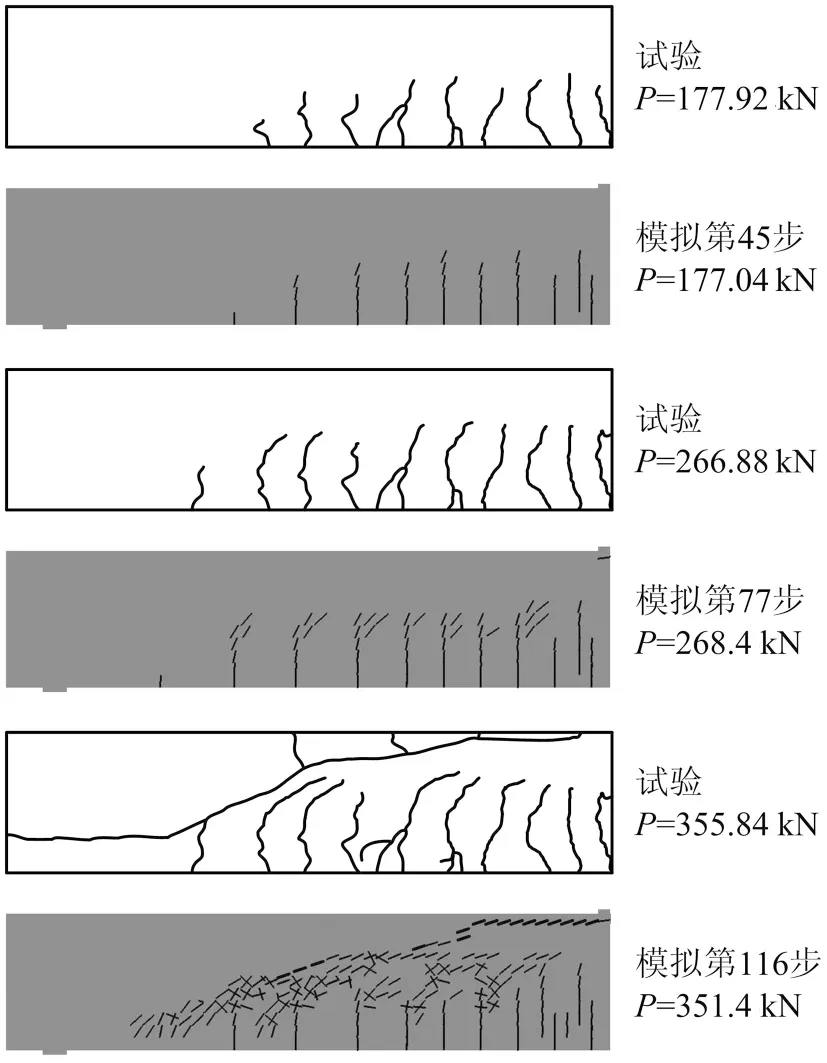
图7 OA-2号试验梁与模拟梁裂缝开展情况对比

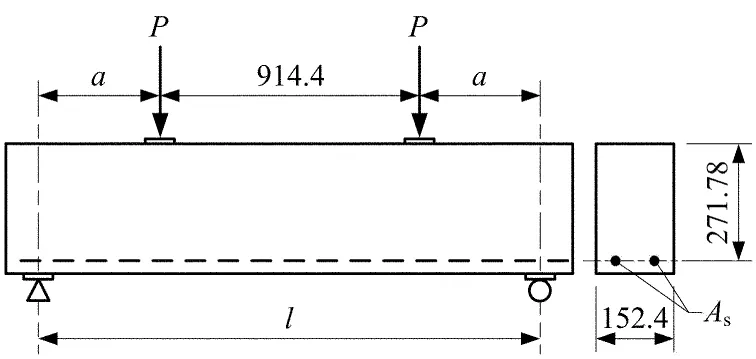
图8 试验梁截面尺寸及荷载布置(单位：mm)

表1 试验梁分组情况Tab.1 The series of experimental beams

根据试验结果，Kani在三维坐标系下提出了“剪切破坏谷”的概念，如图9.“剪切破坏谷”直观地表现了剪切强度和弯曲强度分别控制的区域.从图中可以看出，纵筋配筋率较高时，谷较深且宽；随着纵筋配筋率降低，谷变浅，最后消失.“剪切破坏谷”的谷底位于剪跨比大约为2.5的位置，是剪压破坏和斜拉破坏的转换区间.通常也认为“剪切破坏谷”反映了无腹筋梁的抗剪机理随剪跨比的变化.

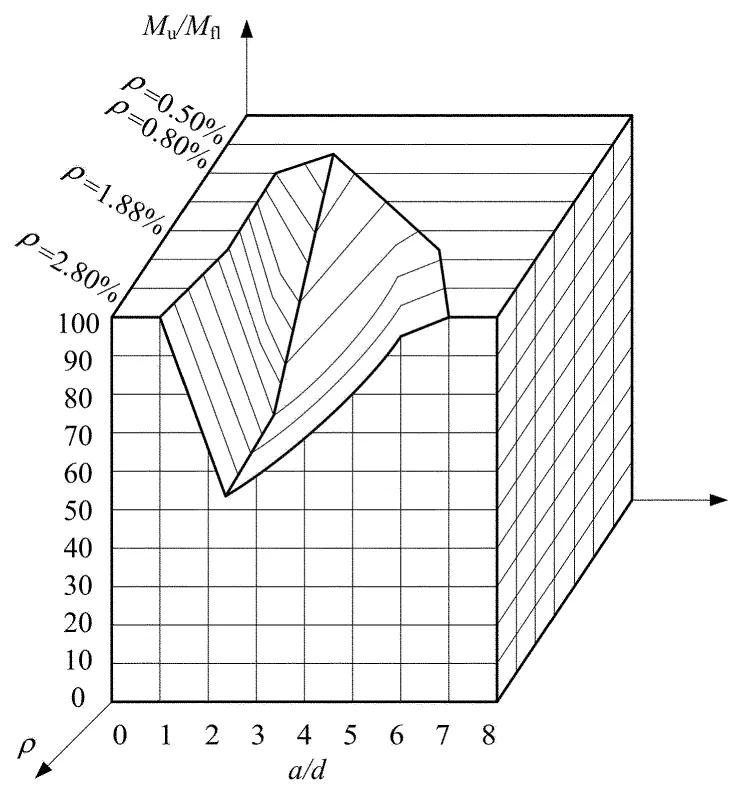
图9 剪切破坏与弯曲破坏的关系：剪切破坏谷

2.2 有限元模型

材料模型与1.2节相同，模型梁截面尺寸以及荷载布置情况均按试验实际情况设置.由于文献[2]中仅给出混凝土抗压强度、钢筋屈服强度，其余材料参数均按照软件默认公式计算结果.按Kani试验实际情况，模拟梁加载处与支座处设置钢垫板，尺寸为152.4 mm×100 mm×20 mm.根据试验梁对称性，建立1/2模型，支座与对称截面约束同Bresler-Scordelis梁.以132号梁(17.24-1.88)为例，模型图如图10所示.单元尺寸大小取为0.05 m，加载方式采用位移控制.

图10 132号简支梁1/2模型

3 有限元模拟结果与分析

3.1 有限元模拟结果与试验结果对比

仍以132号梁为例，对比模拟分析与试验结果.根据文献[2]，试验梁极限荷载为51.98 kN，而ATENA分析结果，模拟梁极限荷载为49.61 kN(第30步)，相对误差约为4.559%，在可接受的范围内.

试验梁破坏时的裂缝分布与模拟梁的对比如图11所示.当荷载增加到几乎与破坏荷载相等时，最外侧的弯曲裂缝迅速连通相邻弯曲裂缝靠近梁顶的部分，并向集中荷载作用点延伸，很快形成临界斜裂缝，梁丧失承载力，发生剪切破坏.由于纵向钢筋拉应力的增大导致钢筋与混凝土之间的粘结应力增大，梁破坏时还出现了沿纵向钢筋的粘结裂缝与撕裂裂缝.另外，由于支座处梁顶受拉，还出现少许短小的裂缝.有限元分析准确地模拟出了试验梁的最后破坏形态.

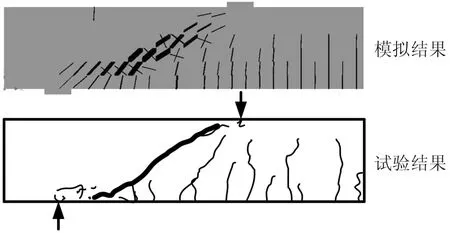
图11 132号试验梁破坏形态模拟

模拟梁计算过程因剪切破坏而突然终止，破坏荷载与出现临界斜裂缝时的荷载相当接近，破坏具有明显的脆性，而根据Kani的试验记录，132号试验梁为Dsu(Sudden Diagonal Failure)，即突然的斜截面破坏，与模拟结果相符.

表2给出每一组试验梁的极限承载力模拟结果与试验结果比值的平均值以及标准差.图12给出133根梁的模拟结果与试验结果的对比.模拟结果的精确性再一次表明，ATENA有限元分析模型能够得到与试验基本相符的结果，建立的有限元模型能够准确地模拟Kani试验梁的破坏荷载.

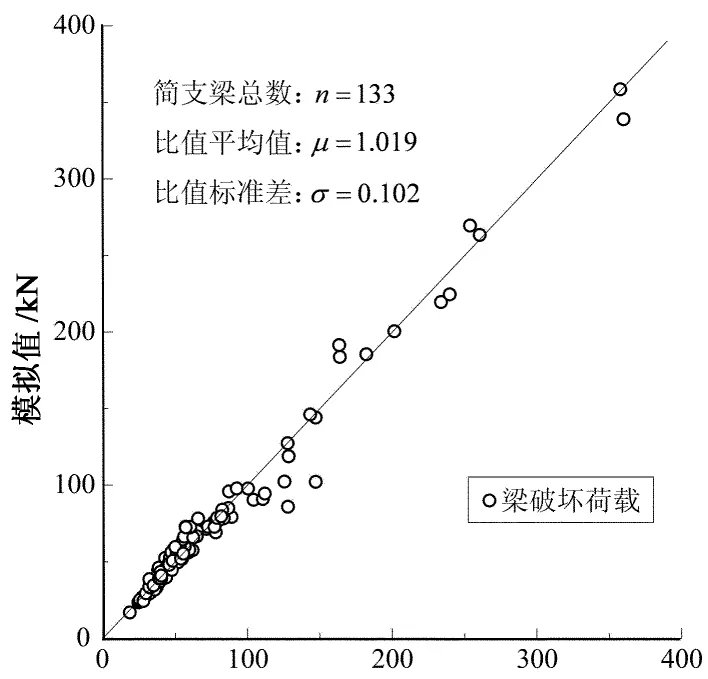
试验值/kN

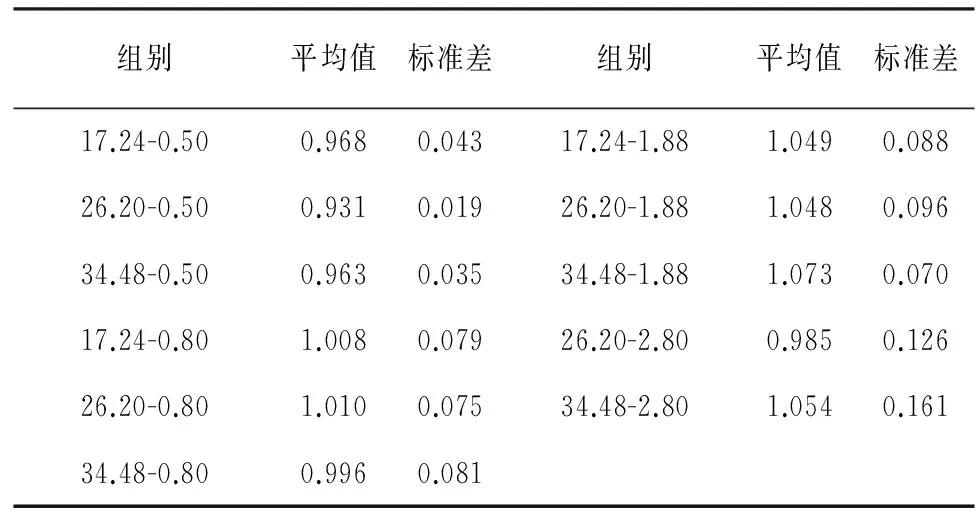
表2 各组梁模拟值/试验值结果的平均值与标准差Tab.2 The average and standard deviation of analytical results/experimental results of each series of beams

图13给出了关于11组共133根梁数值模拟结果的剪切破坏谷与试验结果的对比.图中，纵坐标为梁破坏时截面最大弯矩Mu与梁截面受弯承载力Mfl的比值[2].其中，

Mfl=Asfyd(1-0.4k)，k=Asfy/0.75fcbd

(1)

对于同一试验组相等剪跨比的梁，取最大值和最小值绘制包络线.对比试验与模拟的剪切破坏谷，可见ATENA软件较为准确地模拟出了梁抗剪承载力随纵筋配筋率以及剪跨比的变化规律.

图13 随剪跨比变化的无量纲试验结果与模拟结果对比

3.2 模拟梁名义极限剪应力分析

模拟梁名义极限剪应力数值模拟结果随剪跨比和纵筋配筋率的变化如图14所示.纵坐标采用名义剪应力vu=Vu/bd(Vu为梁的抗剪承载力，b为截面宽度，d为截面有效高度).从模拟结果可以看出，对于不同纵筋配筋率的无腹筋梁，在混凝土强度和剪跨比相同的条件下具有不同的承载力，且配筋率越大，承载力越高.另一个现象是不同配筋率的梁，其受剪承载力随剪跨比变化的程度不同.纵筋配筋率较低的梁，随剪跨比变化的剧烈程度要小于配筋率较高的梁.此外，我们可以发现：当剪跨比小于2.5时，配筋率变化对承载力的影响较大;而当剪跨比大于2.5时，影响较小.总而言之，剪跨比和纵筋配筋率这两个影响因素相互交织，共同影响着梁的抗剪承载力[15].

图14 名义极限剪应力随剪跨比的变化Fig.14 Nominal ultimate shear stress at failure versus a/d

从图14中可以发现，对于相同纵筋配筋率的无腹筋简支梁，名义极限剪应力随剪跨比的增大而减小，且在剪跨比约为2.5处，曲线发生明显转折.名义极限剪应力在梁剪跨比小于2.5时减小幅度较大，剪跨比大于2.5后减小幅度较小.当剪跨比超过2.5后，尽管抗剪承载力减小幅度较小甚至基本保持不变，但随剪跨比的增大，剪跨区段的长度增大，导致破坏弯矩Mu增大.按照上一小节的计算公式，截面最大受弯承载力Mfl仅与截面尺寸、纵筋配筋率、混凝土强度、钢筋屈服强度有关，与剪跨比无关.于是，破坏弯矩与截面最大受弯承载力的比值Mu/Mfl随剪跨比的增大而增大，直到达到1，即截面混凝土和钢筋材料性能得到完全发挥.因此，Kani提出的“剪切破坏谷”出现上升段，见图9和图13.

4 有限元分析结果中的“拱-齿”

4.1 有限元分析结果中的“拱”作用

根据有限元分析结果，以试验组17.24-1.88为例,说明在其他条件都相同的情况下“拱”作用随剪跨比的变化规律.取试验组中剪跨比不同的9根简支梁，图15为9根梁在破坏荷载计算值时的混凝土主压应力云图，所有云图均采用相同尺度，相邻灰度的应力差为0.5 MPa，图中白色部分主应力接近于零.试验组的梁最大主压应力值在15～24 MPa之间，即黑色部分，具体数值见图15.由图可见，随剪跨比的增大，云图中的“拱”形开始渐渐淡化，“拱”部分的混凝土主压应力渐渐减小.即可得出，对于截面尺寸、混凝土强度、纵筋屈服强度、纵筋配筋率等因素相同情况下的无腹筋梁，“拱”作用对梁受剪承载力的贡献随剪跨比的增大而逐渐减弱.通过对其余试验组梁的结果分析，发现均存在此种现象.

4.2 有限元分析结果中的“齿”作用

图15 混凝土主压应力云图(17.24-1.88)

Kani对无腹筋梁抗剪的工作机理提出的“拱-齿”模型是基于公式：

(2)

式中：M为外加荷载承受的弯矩；T为受拉钢筋合力；jd为受拉钢筋合力作用点到受压混凝土合力作用点之间的距离，d为截面有效高度，j为内力臂系数.右式中第一项理解为“齿”作用，代表纵筋拉力合力在临界斜裂缝与梁跨中范围内沿梁长度的变化梯度.

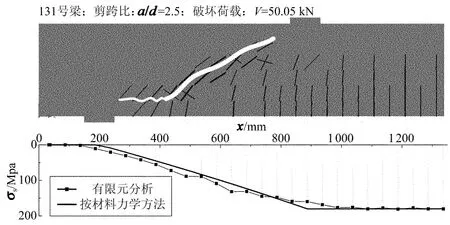
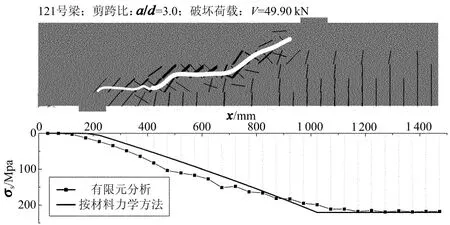
图16 纵向钢筋应力(17.24-1.88)

对图16进一步观察分析，可得出表3中纵筋在临界斜裂缝以及梁跨中处的应力，已知梁截面纵筋配筋面积，从而得出纵筋拉力合力变化值ΔT.根据图16中临界斜裂缝与水平裂缝的交点，可知纵筋处临界斜裂缝到梁跨中的水平距离Δl.从表3中数据可以看出，纵筋拉力合力沿梁长度的变化梯度ΔT/Δl随剪跨比的增大而增大.这说明，对于截面尺寸、混凝土强度、纵筋屈服强度、纵筋配筋率等因素相同情况下的无腹筋梁，随剪跨比的增大，“齿”作用对梁受剪承载力的贡献将会逐渐增大.对于其余试验组梁，纵筋拉力合力变化也存在这种现象.

表3 纵向钢筋应力结果分析

Tab.3 The analysis of longitudinal reinforcement stress results of numerical analysis

梁号剪跨比a/dσs/MPaσs/MPaσs-σs/MPaΔl/mmΔT/kNΔT/Δl/(kN·m-1)1312.572.34180.30107.9690084.0793.41121382.59217.80135.211050105.29100.27122494.71276.50161.901150126.07109.621335112.40366.50254.101450197.86136.46

5 结 论

通过对Kani试验11组共133根无腹筋钢筋混凝土简支梁的非线性有限元模拟分析，证明了Kani提出的“拱-齿”模型.得到如下主要结论：

1) 基于ATENA软件，通过合理选择非线性本构关系及相关参数，本文建立的有限元分析模型准确地模拟了Bresler-Scordelis梁的非线性全过程宏观受力行为和破坏特征，说明采用非线性有限元分析方法研究钢筋混凝土梁受剪性能是可行的.

2) 采用经过校验的有限元模型计算Kani的133根试验梁，所得结果与试验值较为吻合.从计算分析的角度再现了剪跨比和纵筋配筋率等因素对梁的受剪承载力的影响，从而形成进行“拱-齿”模型应力分析的基础.

3) 基于非线性有限元模型的应力分析表明，随剪跨比的增大，“拱”作用对梁受剪承载力的贡献逐渐减小，而“齿”作用对梁受剪承载力的贡献逐渐增大.小剪跨比梁的受力以“拱”为主，大剪跨比梁的受力以“齿”为主.当剪跨比小于2.5时，抗剪承载力减小幅度较大，剪跨比超过2.5后，抗剪承载力减小幅度较小甚至基本保持不变，但随剪跨比增大，剪跨区段长度增大，破坏弯矩增大，Mu/Mfl增大，因此，Kani谷出现上升段.

受ATENA软件及研究水平所限，本文分析没有考虑混凝土结构的随机性和剪切裂缝的局部特性，今后值得进一步深入研究.

Nonlinear Finite Element Analysis of RC Beams without Web Reinforcement by Using ATENA

YI Wei-jian†, WU Yu-yu

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China)

Bresler-Scordlis beam was numerically analyzed to verify a finite element model proposed by ATENA. The simulated damage process and failure mode of Bresler-Scordlis beam and the experiment result are in good agreement. Then, 133 beams of Kani test were analyzed with the verified model. The ultimate load of simulated beams agrees well with the experiment data. From the further analysis of the simulation results of Kani beams, it can be found that the shear capacity contribution of arch action grows and the shear capacity contribution of teeth action reduces as the shear-span ratio increases. The nominal ultimate shear stress of the beams decreases with the increase of shear-span ratio. The curve turns obviously at the shear-span ratio of 2.5. The degree of the reduction before the turning point is larger than that after the point. When the shear-span ratio is larger than 2.5, the shear resistance of the beams with similar factors reduces slowly or even almost remains constant. However, the length of the shear span increases due to the growth of shear-span ratio. As a result, the maximum moment at failure increases, as well as the ratio of the moment and full flexural capacity. Hence, "The valley of shear failure" proposed by Kani has a rising branch as the shear-span ratio is greater than 2.5.

beam without web reinforcement; nominal ultimate shear stress; “arch-teeth” model; finite element analysis; ATENA

2014-11-14

国家自然科学基金资助项目(51178175,51338004), National Natural Science Foundation of China (51178175,51338004)

易伟建(1954-)，男，湖南黔阳人，湖南大学教授，博士生导师

†通讯联系人，E-mail:wjyi@hnu.edu.cn

1674-2974(2015)11-0001-09

TU375.1

A