输电塔线体系风致覆冰脱落动力响应的研究*

杜运兴，卢心龙

(湖南大学 土木工程学院，湖南 长沙 410082)

输电塔线体系风致覆冰脱落动力响应的研究*

杜运兴†，卢心龙

(湖南大学 土木工程学院，湖南 长沙 410082)

建立了两塔三线模型，采用数值实验研究了输电线路的动力特性和中跨覆冰导线发生舞动时覆冰脱落、覆冰不脱落这两种工况的输电塔线系统的动力响应特性，探讨了不同风速下二者响应的差异.计算模型考虑了输电线的初始变形和初始应力.分析结果表明，塔端不平衡张力和邻跨导线横向振幅都随着风速的增加而增大，舞动导致的覆冰脱落使邻跨导线横向振动频率大幅增加，竖向回弹高度相对减小，而中跨的竖向回弹高度和横向振幅分别增加了73.9%和57.7%左右.舞动导致的覆冰脱落对线路的影响不容忽视，在实际线路的设计中应加以特别的考虑.

输电线路；有限元；风；脱冰；舞动

覆冰输电塔线体系在气温升高、风力以及其它环境因素的作用下会出现覆冰的不均匀和不同期脱落.覆冰脱落时将会对导线、地线、绝缘子、杆塔构件以及输电塔等产生动力冲击作用.近年来，国内外学者对导线脱冰进行了大量的研究.Mirshafiei F等[1]建立了六塔五线输电塔线耦合体系有限元模型，并分析了覆冰脱落和导线断线共同作用下体系的动力响应，但是模型中没有考虑空气中气流的作用.实际上覆冰输电导线这一细长的构件还会因空气中气流的自激作用，产生低频、大幅、不稳定、纯弯曲的舞动.导线的舞动会造成相间短路、绝缘子闪络，引起线路跳闸、绝缘子和金具损坏、导线断线、杆塔松动甚至倒塔等严重事故.目前，覆冰导线舞动的机理和模型主要有：DenHartog[2]提出的忽略导线扭转运动的垂直舞动机理、Nigol等[3]提出的考虑垂直方向气动力和导线扭转运动的扭转激发舞动机理和YU P等[4]提出的考虑垂直方向气动力、扭转力、偏心惯性对舞动影响的偏心惯性耦合失稳机理.李欣业等[5]等考虑基于输电导线垂向和扭转振动耦合的两自由度模型,利用多尺度法和数值分析方法,分别就系统参数和环境参数对临界风速和舞动振幅的影响进行了理论分析；王丽新[6]等利用梁单元模拟覆冰导线，通过动坐标迭代法和Newmark法进行静力、动力响应分析，给出了高压输电线舞动的有限元分析方法，然而对于输电塔的耦合作用和舞动过程中覆冰的脱落均未有涉及.杜运兴[7]等分析了塔线体系在风荷载和覆冰荷载共同作用下对塔端不平衡张力造成影响的各种因素并提出了二者共同作用下计算不平衡张力的理论公式，但对系统的动力响应特性未做探究.

针对在实际运行线路中导线舞动时伴随着覆冰脱落的情况，本文采用数值实验的方法建立了塔线体系的耦合模型，通过覆冰破坏准则的定义，对覆冰线路发生舞动导致覆冰脱落时体系的动态响应进行了探讨和分析，以期为覆冰线路的设计提供参考.

1 有限元模型

1.1 输电塔线体系结构及材料参数

为了研究导线舞动导致的覆冰脱落对输电线路的影响，本文选用5B-ZBC1酒杯型铁塔建立了二塔三线的三维有限元模型，如图1～2所示.输电塔架的所有杆件均采用空间梁单元,考虑到导线具有一定的抗扭刚度并承受一定扭矩，对导线采用忽略剪切变形的弹性梁单元来模拟.针对导线抗拉不抗压的性质，利用软件中的亚弹性材料定义其拉压方向的应力应变关系曲线来实现这一特性，即当ε大于0时，弹性模量E取导线的实际弹性模量；当ε小于0时，弹性模量E取为0.导线外侧的覆冰采用基于欧拉伯努利梁理论的闭合截面梁单元模拟.覆冰单元采用与导线共节点的方式建立.绝缘子串一端与输电塔横担铰接，另一端与导线铰接，利用刚性连接连接横担及导线对应点，约束三个平动自由度来模拟，如图3所示.关于5B-ZBC1输电塔的具体几何尺寸均参照文献[8]建立，导(地)线的具体参数如表1所示.

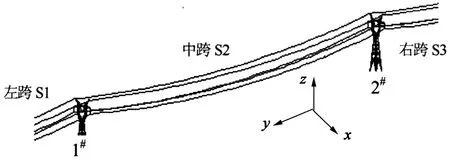
图1 输电塔线体系图

图2 5B-ZBC1型输电塔

图3 绝缘子两端连接示意图

表1 导(地)线的型号及参数Tab.1 Parameters of wire

覆冰的破坏准则目前所见有两种，一是文献[9]提出的等效塑性应变破坏准则；二是文献[10]提出的拉伸强度破坏准则.文献[11-12]通过冷风洞模拟大气结冰，测得冰的弯曲强度、等效模量和压缩强度.当覆冰厚度不大时，其剪切变形可以忽略，认为覆冰的破坏采用最大拉应力理论较合理，故本文采用拉伸强度理论.根据沈国辉[13]等的分析，本文的覆冰弹性模量取E=1.0×109N/m2，拉伸强度取0.9 MPa，冰密度取900 kg/m3.导线和杆塔的阻尼采用瑞利阻尼模型，即

C=αM+βK．

(1)

式中：α和β为瑞利阻尼系数.根据文献[14]中的分析，β通常很小，可以近似为0.对于覆冰导线和杆塔，α可分别取为0.1和0.2.计算模型采用的材料本构模型均为线弹性模型，计算过程中考虑整个体系的几何非线性.

1.2 导(地)线的形态和应力

输电塔线体系的动态响应都是在初始静态构型的基础上进行的，所以在进行导(地)线的动力分析前，导(地)线形态的确定和应力的施加尤其重要.架空线路导线在其自身重力作用下初始形态如图4所示，其构型可用下述悬链线方程[15]表示.

(2)

该方程的解为：

(3)

(4)

(5)

导线长度：

(6)

式中：q为沿导线长均布荷载(N/m)；c为两悬点的高差(m)；l为档距(m)；H为导线最低点的张力(N)由设计给定.本文档距l取440 m，H取23.21 kN，高差c为0，弧垂f为14.09 m(初始垂跨比为3.2%).为了在有限元模型中实现满足导线几何形态的同时满足相对应的应力状态，采用下述方法：根据文献[16]，导线的伸长量(式中A为导地线截面面积)：

(7)

无应力状态时导线的长度：

s=s0+Δs．

(8)

在最低点张力H已知的情况下可根据式(4)和(5)求出α和β，进而可根据式(7)和(8)求出无应力状态时的状态方程.以无应力时的状态方程建模再施加导线的自重荷载进行静力分析，即可达到在导线上施加相对应的应力的目的.

图4 自重作用下输电导线的形态

2 荷载分析

2.1 风荷载

2.1.1 导(地)线所受风荷载

当风吹过在垂直其方向上处于微振动状态的覆冰导(地)线时，导(地)线会因风的自激作用产生弯曲的大幅振动，振动激发的波会在两个输电塔之间快速传递，通常振幅可达导线直径的10倍以上.风作用于覆冰的导(地)线上相当于对其施加了3个分力[17]：阻力FD,升力FL和扭矩FM，如图5所示.这3个分力的表达式如下：

(9)

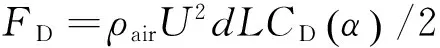
(10)

(11)

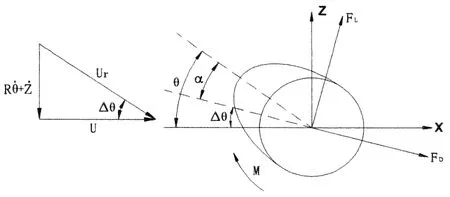
图5 导线舞动时相对攻角

α/rad

如图5所示，作用在导(地)线上的三分力投影到整体坐标系上的分力即为(FM不变)：

Fx=FL·sinΔθ+FD·cosΔθ；

(12)

Fz=FL·cosΔθ-FD·sinΔθ．

(13)

从以上两式可以看出导线在舞动过程中，作用于其上的气动荷载时刻在改变.本文通过子程序在每一步计算之前根据上一步的计算结果调整三分力系数，以实现气动荷载的实时施加.

2.1.2 输电塔所受风荷载

将塔所受风载集中等效在若干节点上,节点具体位置参见文献[7]，施加点风载按式(14)计算，采用指数型风剖面描述平均风速沿高度的变化规律.

(14)

式中:Ft为输电塔荷载施加点处风荷载值(N)；μs为构件体型系数，取2.5；As为塔承受风压投影面积计算值(mm2)；V为风载施加点高度处风速(m/s)；B是覆冰时风荷载增大系数[19].

2.2 导(地)线覆冰荷载

在静力分析时，覆冰单元处于“杀死”状态，将覆冰荷载等效为重力荷载来进行初始找形的静力平衡分析，以得到导(地)线在自重作用下的初始构型.在动力分析时，将覆冰单元“激活”以考虑覆冰的质量和刚度.静力分析时覆冰的重力等效荷载采用公式(15)计算：

(15)

式中：q为单位长度上的覆冰荷载(N/m)；d为导线的直径(mm)；b为覆冰厚度(mm)；γ为覆冰重度(kN/m3)，取8.82 kN/m3.

3 塔和塔线体系动力特性分析

本文在不考虑导(地)线对输电塔影响的情况下，首先对单塔进行了模态分析，其次分析了塔线耦合体系的动力特性，得到了单塔和塔线体系的自振频率和振型.限于篇幅,仅列举其前4阶的频率(如表2～3所示)和振型(如图7～8所示).

表2 输电塔动力特性

Tab.2 Dynamic characteristics of transmission tower

阶数频率f/Hz周期T/s振型主要特征11.80780.5532绕x轴一阶弯曲21.81890.5498绕y轴一阶弯曲32.57290.3887绕z轴一阶扭转45.42110.1845绕x轴二阶弯曲

表3 输电塔线体系动力特性

Tab.3 Dynamic characteristics of the system

阶数频率f/Hz周期T/s振型主要特征10.14446.9252xy面内正对称20.14746.7843xy面内反对称30.14746.7843xy面内正对称40.14746.7843xy面内正对称

(a)第一振型

(b)

图8 输电塔线体系前四阶振型

上述动力特性的分析结果表明，模型采用的输电塔在x，y方向的频率较为接近，因此输电塔在这两个方向上的整体刚度相差不大.本文提取了塔线体系的前800阶模态，发现塔线体系前600阶模态振动频率较为密集，且基本以导线振型为主而输电塔的振型分辨不清，600阶以后才出现可分辨的输电塔振型，这与文献[20]的分析结果较为一致.

4 舞动过程中覆冰脱落动力分析

为了探讨覆冰输电线路舞动过程中，覆冰脱落对体系动力响应的影响.本文以档距440 m，覆冰厚度15 mm，初始风攻角24°，无高差的三档线路为对象，首先分析了输电塔对导线舞动的影响，其次进行了舞动过程中脱冰与不脱冰两种情况下动力响应的对比分析，并探讨了不同风速下二者动力响应的差异.与耐张塔连接的边跨导线端点只发生很小的位移，将耐张塔简化为铰支座，地基对杆塔的约束按固结处理.具体计算工况为工况1：中跨线路发生舞动，体系无覆冰脱落；工况2：中跨线路发生舞动，中跨线路有覆冰脱落；工况3：中跨线路发生舞动，体系无覆冰脱落，输电塔以铰支座代替.

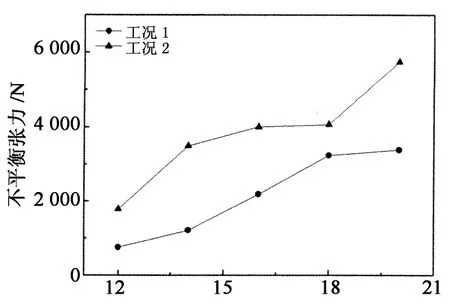
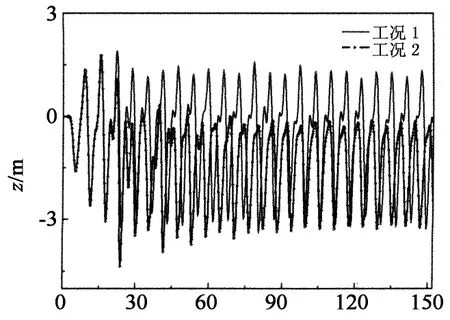
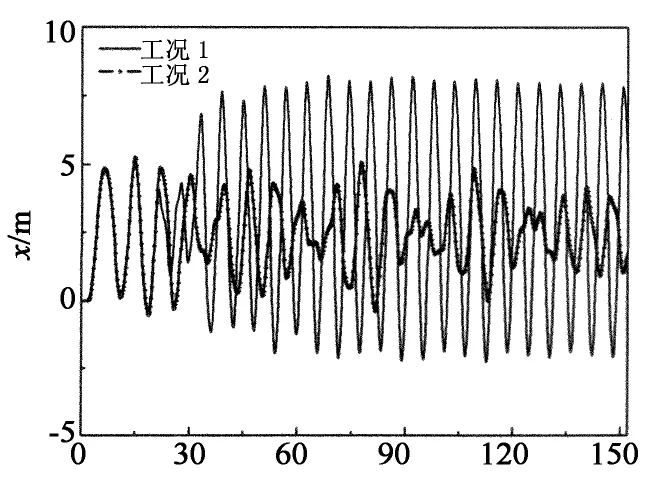
计算了在12～20 m/s的风速范围内，3种工况下的动力反应并从顺导线方向的最大不平衡张力、跨中中点横向和竖向的位移时程、振幅等方面进行了对比分析.具体的结果如图9～15所示，其中图11～15所示曲线为风速在16 m/s时各种工况下位移时程曲线相互对比图(以导线覆冰后的平衡位置作为零点).图题中的S1C2，S2C2分别表示左跨中相导线和中跨中相导线，时程曲线均取自各跨中点.

时间/s

风速/(m·s-1)

时间/s

从图9的简单比较可以发现，在覆冰线路舞动的分析中，单纯地用铰支座代替输电塔并不可取.图10显示，输电塔上的最大不平衡张力随着风速的增加而逐渐增大，在同一风速下工况2的不平衡张力均比工况1的要大，且随着风速的增大两者之间的差异更加明显.由于本文采用的模型是对称结构，在只有自重和覆冰荷载作用下塔端顺导线方向的初始张力是平衡的，中跨受空气动力作用发生舞动时不平衡张力才开始出现，此时中跨覆冰的脱落加剧了这种力的不平衡性，最大时工况2能达到工况1的2.37倍左右.当导线处于重冰区时，舞动过程中覆冰的脱落导致不平衡力的增加将更明显，严重时有可能超过设计值造成断线事故.

从图11也可以发现：由于中跨舞动导致的覆冰脱落对于边跨的输电导线的横向振幅也有一定的影响，而且趋势与不平衡张力的变化趋势大体一致.

从图12～13可以看出中跨导线舞动导致的覆冰脱落对邻跨导线的竖向和横向振动有着不同程度的影响.中跨发生舞动时，邻跨导线横向的振动开始是发散的，达到最大值后又逐渐收敛，如此交替循环.工况1完成一次循环需要103 s左右，是工况2 16 s的6.4倍，可见覆冰的脱落导致邻跨导线横向的振动频率大幅增加.这可能是由于覆冰脱落导致两侧的绝缘子在不平衡张力的作用下向邻跨摆动，造成邻跨导线出现应力松弛的结果.从图13还可以发现，覆冰脱落后，邻跨导线在横风向上的振幅出现了一定程度的减小，并在较低的平衡位置上下振动.

时间/s

时间/s

图14～15是中跨导线中点在横向和竖向的位移时程图.从图中可以明显观察到：由于该跨覆冰的脱落导致导线在横向和竖向的振幅都大幅增加.横向的最大振幅由5.2 m增加到8.2 m，竖向的最大振幅由6.9 m增加到12 m.覆冰的脱落引起中跨相对于邻跨的竖向荷载和侧向刚度的减小应该是导致这些变化的直接原因.

时间/s

时间/s

5 结 论

本文建立了二塔三线的连续档输电塔线体系舞动有限元模型，讨论了体系的动力特性和输电塔对导线舞动的影响，并分析了在中跨导线发生舞动时覆冰发生脱落和不脱落时系统响应的区别并得到以下结论：

1)本文采用的输电塔在横向和侧向两个方向的刚度较为接近，塔线体系这种复杂结构的振动频率较为密集，低阶振型以导线振型为主，而以输电塔为主的振型均出现在高阶模态中.覆冰导线舞动的分析中输电塔并不能简单采用铰支座来代替.

2)当中跨发生舞动时，塔端不平衡张力和邻跨竖向振幅都随着风速的增加而逐渐增大，且在同一风速情况下工况2比工况1的值都要大，最大分别达到2.37倍和1.3倍左右.当线路处于重冰区并遭遇大风天气时，舞动过程中覆冰的脱落导致不平衡力的增加将更明显，甚至有可能超过设计值造成断线事故.

3)舞动导致的覆冰脱落使中跨的竖向和横向振幅均出现较大程度的增长并维持在一个较高的平衡位置上振动，覆冰的脱落致使中跨横向振幅增加了57.7%，跨中回弹高度增加了73.9%．这一现象持续发展可能会引起导线之间的触碰造成相间短路.舞动导致的覆冰脱落使邻跨导线横向振动频率大幅增加而竖向回弹高度相对减小.以上结论说明舞动导致的覆冰脱落对线路的影响不容忽视，在实际线路的设计中应该加以特别的考虑.

[1] MIRSHAFIEI F，MCCLURE G， MASOUD F. Modelling the dynamic response of iced transmission lines subjected to cable rupture and ice shedding[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 948-954.

[2] DEN HARTOG J P. Transmission line vibration due to sleet[J].AIEE Transmission,1932,51(4): 1074-1086.

[3] NIGOL O, BUCHAN P. Conductor galloping—part Ⅱ torsional mechanism[J].IEEE Transmission on Power Apparatus and System，1981，100(2)：708-720.

[4] YU P, SHAH A H, POPPLEWWELL N. Inertially coupled galloping of iced conductors[J].Transmission of the ASME,1992，59(1)：140-145.

[5] 李欣业,张华彪,侯书军,等. 覆冰输电导线舞动的仿真分析[J]. 振动工程学报,2010,23(1):76-85.

LI Xin-ye, ZHANG Hua-biao, HOU Shu-jun,etal. Theoretical and numerical analysis of galloping of iced power transmission lines[J].Journal of Vibration Engineering, 2010,23(1):76-85. (In Chinese)

[6] 王丽新,杨文兵,杨新华,等. 输电线路舞动的有限元分析[J]. 华中科技大学学报:城市科学版,2004, 21(1):76-80.

WANG Li-xin, YANG Wen-bing, YANG Xin-hua,etal. Finite element analysis for galloping process of transmission lines[J].J of HUST:Urban Science Edition, 2004,21(1):76-80. (In Chinese)

[7] 杜运兴,孙倩. 山区覆冰输电塔线体系风致不平衡张力的研究[J]. 湖南大学学报:自然科学版,2014,41(4):72-77.

DU Yun-xing, SUN Qian. Analysis of the wind-induced unbalance tension of iced transmission tower-line system in mountains areas [J].Journal of Hunan University: Natural Sciences, 2014,41(4):72-77. (In Chinese)

[8] 刘振亚.国家电网公司输变电工程典型设计500 kV输电线路[M].北京：中国电力出版社，2005:188-191.

LIU Zhen-ya. Power transmission project typical design of state gird corporation of China 500 kV transmission line branch[M]. Beijing: China Electric Power Press, 2005: 188-191. (In Chinese)

[10]DRUEZ J, LOUCHEZ S, BOUCHARD G. Study of ice-shedding phenomenon on cables[C]//Proceeding of the 9th International Conference of offshore

[11]PHAN C L，MOCOMBER P. Adhesion of rime and glaze on conductors protected by variousmaterials[J]. Transactions CSME, 1976, 4(4): 204-208.

[12]LAFORTE J L，PHAN C L. Adhesion of ice on aluminum conductor and crystal size in the surface layer[R]. Alaska: CRREL Special Report, 1983: 83-91.

[13]沈国辉,徐晓斌,楼文娟,等.导线覆冰脱冰有限元模拟方法的适用性分析[J]. 工程力学,2011,28(10):9-15.

SHEN Guo-hui, XU Xiao-bin, LOU Wen-juan,etal. Applicability analysis of finite element methodologies to simulate the ice-accreting and ice-shedding on transmission lines [J]. Engineering Mechanics, 2011,28(10):9-15. (In Chinese)

[14]胡位勇,严波,程皓月,等.输电塔线体系断线动力响应及杆塔破坏模拟研究[J].应用力学学报,2012,4(29):431-436.

HU Wei-yong, YAN bo, CHENG Hao-yue,etal. Numerical investigation on dynamic response and failure of transmission line and tower after wire breaking [J].Chinese Journal of Applied Mechanics, 2012,4(29):431-436. (In Chinese)

[15]沈世钊,徐崇宝,赵臣.悬索桥结构设计[M]．北京：中国建筑工业出版社,1997:67-99.

SHEN Shi-zhao, XU Chong-bao, ZHAO Chen. The structural design of suspension bridges[M]. Beijing: China Architecture & Building Press, 1997:67-99.(In Chinese)

[16]廖圆圆,李周,王荣辉,等. 精确索单元法在找形及无应力索长计算中的应用[J]. 中外公路,2011, 31(6):33-37.

LIAO Yuan-yuan, LI Zhou, WANG Rong-hui,etal. Applications of accurate cable element method in form finding and unstressed cable length calculation[J]. Journal of China & Foreign Highway, 2011, 31(6):33-37. (In Chinese)

[17]MCCOMBER P, PARADIS A. A cable galloping model for thin ice accretions[J]. Atmospheric Research, 1998, 46(1): 13-25.

[18]楼文娟,杨伦,潘小涛. 覆冰导线舞动的非线性动力学及参数分析[J]. 土木工程学报,2014, 47(5):26-33.

LOU Wen-juan, YANG Lun, PAN Xiao-tao. Nonlinear dynamics and parametric analysis for galloping response of iced conductor[J].China Civil Engineering Journal, 2014, 47(5):26-33. (In Chinese)

[19]GB50545-2010 110～750 kV架空输电线路设计规范[S].北京：中国计划出版社，2010: 28-31.

GB 50545-2010 Code for design of 110～750 kV overhead transmission line[S]. Beijing: China Planning Press, 2010: 28-31. (In Chinese)

[20]李喜来,王开明,尹鹏.大跨越输电塔动力特性[J].电力建设,2010, 5(31):43-48.

LI Xi-lai,WANG Kai-ming,YIN Peng.Dynamic behavior of large-span power transmission tower[J]. Electric Power Construction,2010, 5(31):43-48. (In Chinese)

Research on Dynamic Response of Wind-induced Ice-shedding of Transmission Tower-line System

DU Yun-xing†，LU Xin-long

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China)

Wind-induced ice-shedding makes transmission-line tower system produce complex dynamic responses. This paper built a finite element model of a three-span transmission-line system. When galloping occurs in mid-span conductors, with or without ice-shedding, the dynamic responses of the transmission-line tower system were analyzed through numerical experiment, and the differences of the two load cases under different wind speeds were also studied. Besides, this paper also analyzed the dynamic characteristics of the system. In the model, the initial deformation and stress of the conductors is taken into account. The results show that the unbalanced tension of the tower head and the transverse conductor-amplitude of adjacent spans get larger with the increase of wind speed. The transverse vibration frequency of adjacent-span conductors led by ice-shedding increases dramatically, and the vertical rebound height decreases relatively. The vertical rebound height and transverse amplitude of the mid-span increase by about 73.9% and 57.7% respectively, to which special attention should be paid in the design of transmission lines.

transmission line；finite element method；wind；ice-shedding；galloping

2014-12-15

国家自然科学基金资助项目(51261120374，51378199),National Natural Science Foundation of China(51261120374，51378199)

杜运兴(1971-)，男，河南平顶山人，湖南大学副教授，博士

†通讯联系人，E-mail:duyunxing@hnu.edu.cn

1674-2974(2015)11-0088-07

TM75

A