二维多相式相位信号参数估计降维算法及仿真
廖建庆, 郑乃清, 黄李健
(宁德师范学院 物理与电气工程系,福建 宁德352100)
二维多相式相位信号(PPS)是雷达通信信号处理领域的一个非常重要的非平稳信号模型,在复杂二维非齐次双通道信号建模和合成孔径雷达干涉测量方面已有广泛的应用[1]。
二维多相式相位信号参数估计通过与估计函数相结合过程来完成对信号参数的估计,该处理过程可分为两个阶段,分别为粗估阶段和细化阶段。粗估阶段表示将未处理信号通过简单处理后获得的最大粗估位置,即通过计算估计函数或迭代方法对粗估阶段信号依次进行细化分解。应用估计函数方法是由Friedlander 和Francois 首次提出[2],被称为Francois-Friedlander(FF)算法。在FF 算法中,将初始信号转换为二维复杂正弦函数,其频率正比于相位参数值,由此为参数估计提供新的依据。该算法对文献[3]中迭代算法起到重要作用。但是,FF算法在参数估计中,其均方差很难达到Cramér-Rao下界(CRLB)即该算法精度不是很理想,而且在高阶PPS 条件下具有较高的信噪比和较大的估计误差,并且信噪比和估计误差会随着PPS 阶数的增加而变大。文献[4]提出一种二维立方相位函数估计方法(CPF),CPF 算法在信噪比方面远优于FF 算法,文献[5]已将该算法应用到五阶PPS 参数估计。直接研究二维PPS 参数估计的计算量很大,但文献[4-5]利用遗传算法有效降低了参数估计运算时间,然而遗传算法的引入又给高信噪比带来不必要的系统误差。
对此,文中提出一种有效计算估计量的二维PPS 参数估计优化算法,即先对粗估计量做滤波相位解(FPU),后对估计量进行细化分解,本优化方法不需要对二维估计函数的粗估计量做最大似然估计,而是通过固定其中一个参量,将二维PPS 看作一组一维PPS,通过对一维PPS 的计算处理,最终完成对二维PPS 的参数估计。基于FPU 参数估计方法如文献[6],该算法在计算上采用了滤波、相位展开的运算形式,整个算法的计算量显著减少。通过对二维多相式相位信号进行参数估计仿真实验,结果显示了本算法的有效性。
1 信号模型和一般估计方法
二维多相式信号模型如下:

其中
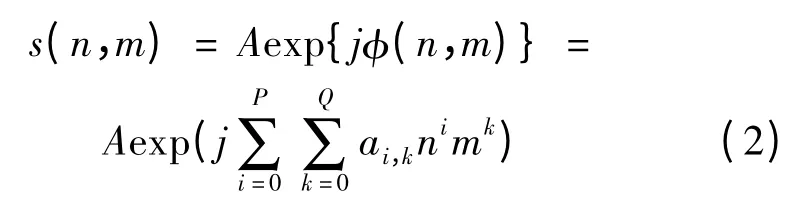
式(2)中,A 为信号的振幅,φ(n,m)为相位参数ai,k的P 阶和Q 阶的二维多相式函数;式(1)中,v(n,m)是均值为0 和方差为σ2v 的二维高斯白噪声。文中目的是要估计二维多相式信号x(n,m)中的相位参数ai,k,0 ≤i ≤P,0 ≤k ≤Q。
目前对信号s(n,m)参数估计最常用的方法是文献[2]提出的FF 算法,该算法是将信号s(n,m)转化为一个频率正比于该信号相位参数的二维复正弦信号,因此可以将参数估计归结为一个二维正弦曲线频率估计问题,即对二维信号频谱取最大化,为得到正确二维频谱,可在信号处理过程中增加采样点(但会显著增加计算量)或采用替代方法比如迭代算法[3]。但无伦采用什么方法,FF 算法一般很难达到Cramér-Rao 下界(CRLB),即FF 函数估计达不到满意的估计效果,因此文中提出一种新型的替代算法。
2 提出算法
2.1 算法描述
首先,设信号s(n,m)中的参数m 一定,则二维多相式相位信号便转化为一维多相式:
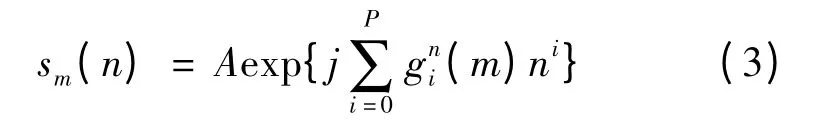
其中
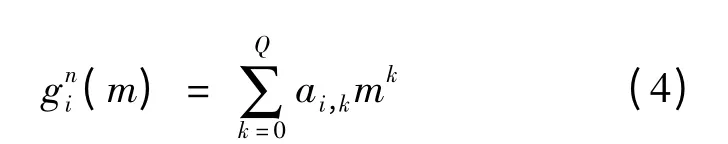
同理,设s(n,m)中的参数n 一定,这样二维多相式相位信号转化为一维多相式相位信号sn(m):
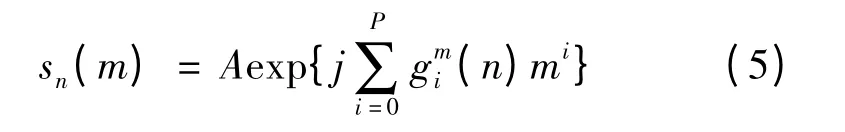
其中
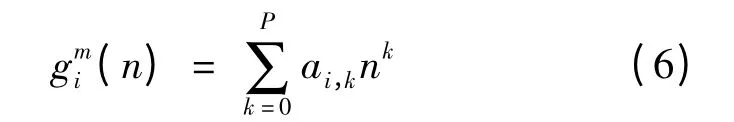
假设参数ai,k的粗估计有效,那么信号估计可以利用FF 算法或一般的二维CPF 方法[5]得到,即如果ai,k的粗估计已知,那么多相式和的粗估计便可得到。
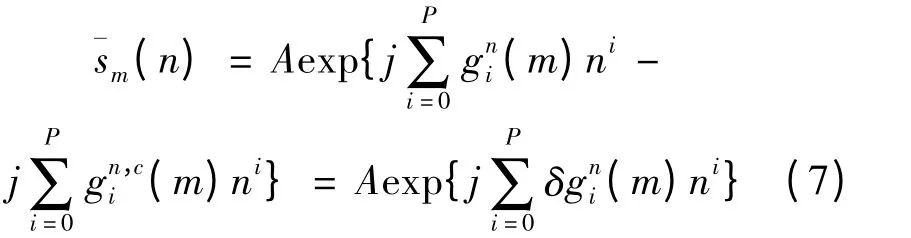
2)对解线性调频信号(移动平均(MA)滤波器长度为LMA)进行滤波处理,目的是获得较高的信噪比;

文中描述的算法可以用FPU[·]运算表示,即当输入的参数是一维多相式相位信号s(n)及对应的初始PPS 参数的向量a 时,则其输出为向量a 经过优化后的参数向量,例如

经过优化参数的向量可以分解为
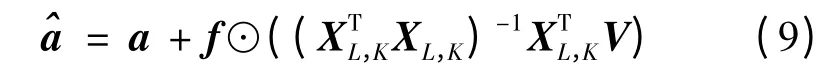
其中,T 为转置算符;⊙为Hadamard 乘积算子
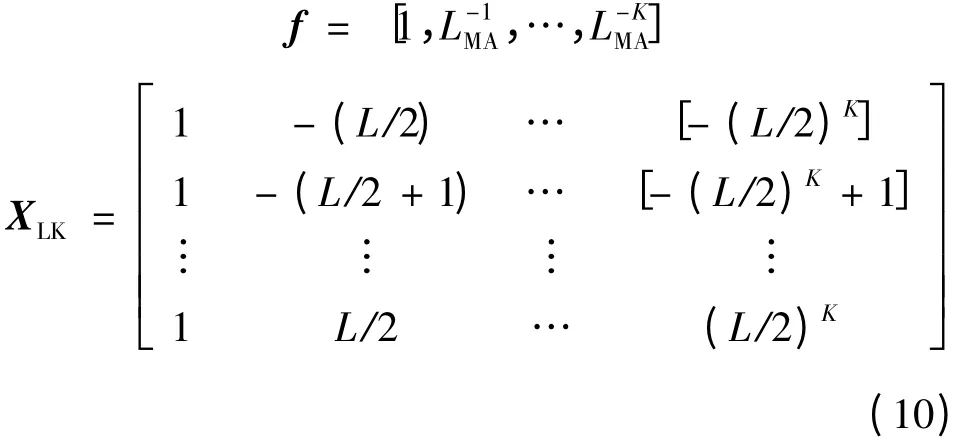
其中:K 为s(n)的PPS 的阶数;(L +1)为解线性调频信号¯s(n)的移动平均滤波器输出长度;V 是¯s(n)的解缠相,文献[6]提出了FPU 实现方法。
2.2 算法实现
For
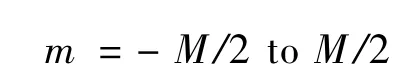
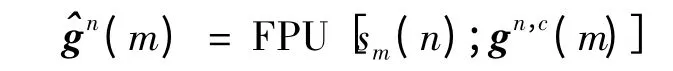
End for
For
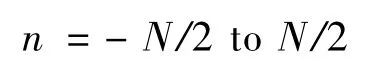
将粗估计向量

用
学校担负着培养学生游泳技能及自救能力的重任,而体育教师是促使游泳教学得以安全进行的执行者,也是校本课程资源的开发者。我们必须在提高他们的专业综合素质同时,充分地挖掘他们的潜力确保校本课程的开展与普及。在调查研究中发现,高中、初中、小学中会游泳的体育教师队伍比例有较大差距,城镇体育教师队伍也有较大差距。因此,我们要加大教师游泳技能与游泳救助技能的培养力度,教育以及相关体育行政部门要加大对体育教师游泳技术教学能力、救生技术培训的力度,把游泳技术、救生技术作为体育老师教学的必备能力之一,使学生更好地掌握救生技术。
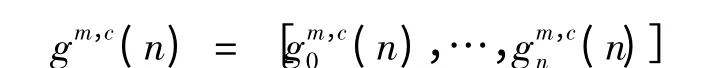
形式表示,而后对gm,c(n)进行优化,得到优化估计向量
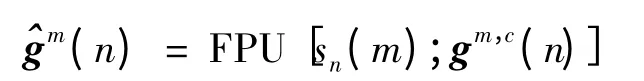
End for
For
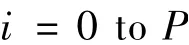
利用多相式回归:
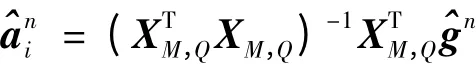
其中XM,Q在式(10)已定义
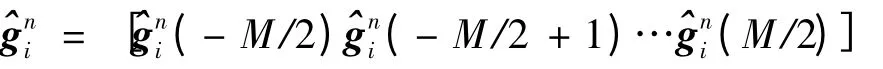
End for
For
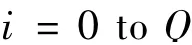
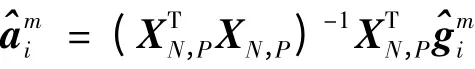
其中XM,Q在式(10)已定义
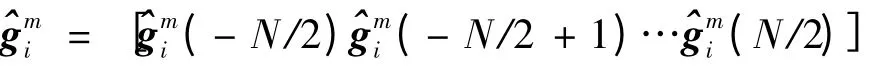
End for
2.3 计算复杂度分析
要考虑一个算法的粗略计算复杂度,只要考虑该算法核心部分的运算次数。在FPU 算法中,主要考虑的是矩阵的运算,即矩阵乘法和矩阵转置运算,而考虑到本算法中的矩阵维数比较小,所以矩阵转置计算量在本算法中不需要考虑。
因此,实际FPU[sm(n);gn,c(m)]和FPU[sn(m);gm,c(n)]需要做○(MP2/LMA)和○(MQ2/LMA)次实数乘法运算,其中○表示最大值符号。由此可见,整个乘法运算次数为○(NM(P2+ Q2)/LMA),比算法[3]在相同条件下的乘法次数○(NMPQ)少,即运算处理速度得到提高。
3 仿真分析
为了验证本算法的有效性,做如下仿真实验,实验信号模型采用三阶的二维PPS 三角形式[2],设信号幅值为1,其阶数为3,信号模型如下。
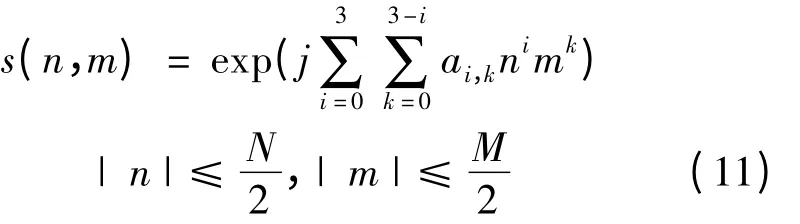
其中

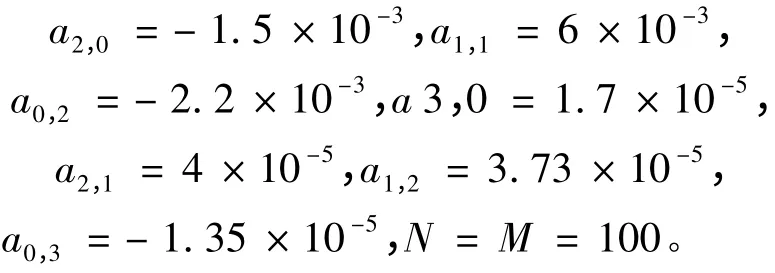
信号中引入均值为0,方差为σ2v 的高斯白噪声v(n,m),信噪比定义为SNR = - 20lgσv。对文中算法(LMA= 11,L =8)和文献[3]给出的优化搜索算法(做3 次迭代)性能进行比较,两种算法都是经过FF算法粗略参数估计得到的粗估计值,对三阶多相式相位信号进行200 次蒙特卡洛仿真实验,仿真结果如图1 ~4 所示。
仿真结果显示估计值a3,0,a0,3,a2,1,a1,2的均方误差(MSE),其中FF 算法仿真曲线用带菱角虚线表示,迭代算法[3]用点线表示,文中算法用实线表示。由仿真结果可见,几种算法的MSE 结果都接近于相应的CRLB(虚线),信噪比阈值都在-4 dB 附近。但是,在高信噪比时,文中算法基本达到了CRLB,而取决于估计参数的迭代算法[3]比CRLB高3 ~4 dB。由此可见,文中算法的参数估计精确度优于其它几种算法。
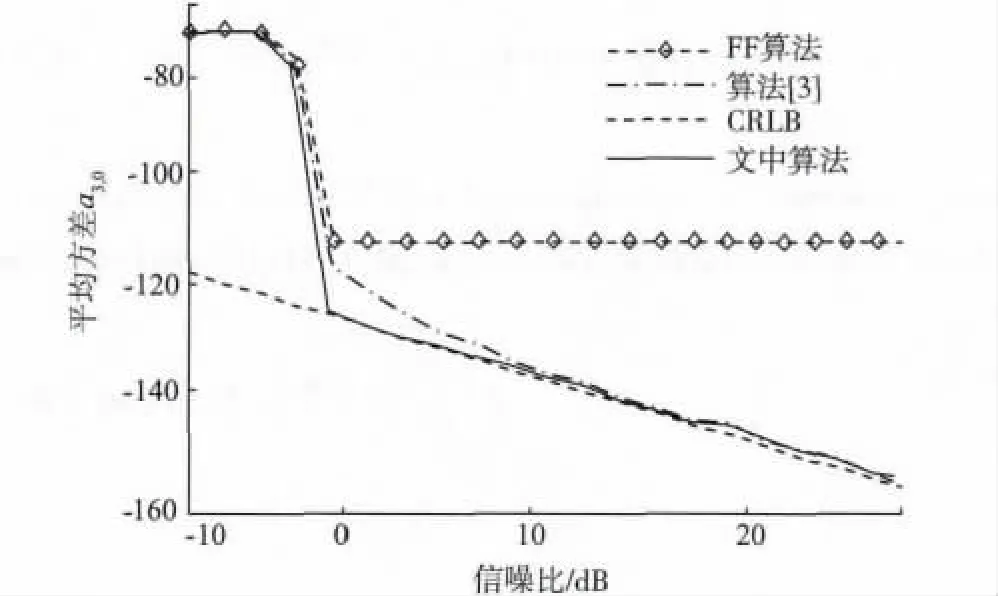
图1 估计值a3,0 时的均方误差Fig.1 Mean squared error of the parameter a3,0
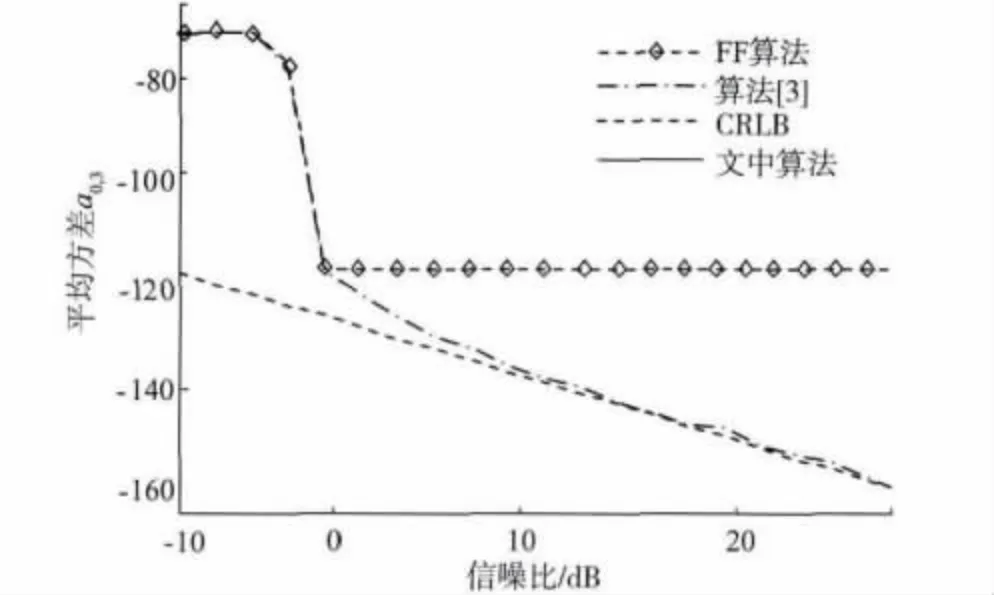
图2 估计值a0,3 时的均方误差Fig.2 Mean squared error of the parameter a0,3
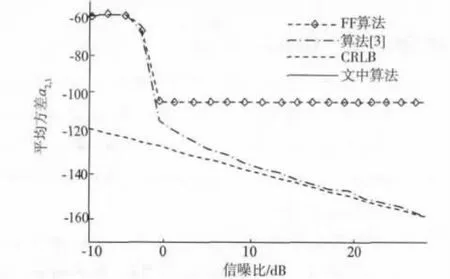
图3 估计值a2,1 时的均方误差Fig.3 Mean squared error of the parameter a2,1
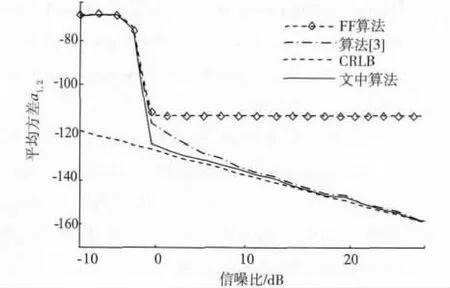
图4 估计值a1,2 时的均方误差Fig.4 Mean squared error of the parameter a1,2
另外,为了进一步提高在较低信噪比的情况下,参数估计的均方误差接近Cramér-Rao 下界,文献[7-8]采用了傅里叶系数插值的频率估计算法,用以提高该方法的运算速度。虽然该算法在一定程度上改进了信号计算的精确度,但其运算复杂度随着多相式估计信号的维数增加而变得更为复杂,由此降低算法的运算速度,进而影响算法的估计精度。文中提出的降维算法正好解决了这一难题,为多维多相式参考估计提供新的思路。
对信号的参数优化,一般来说是采用迭代加梯度模式,首先对信号进行粗估计,再对信号做最大似然化处理,这种方法在一维PPS 参数估计中得到应用[9]。
4 结 语
文中提出一种基于一维滤波相位解的二维PPS参数估计的优化算法,该算法在精确度和计算复杂度方面都要优于其它信号参数估计算法。仿真结果说明,在高信噪比时,其估计算法接近于CRLB,但是渐近效率分析还有待进一步研究。
[1]杨科,廖桂生,徐青.旋转式合成孔径雷达干涉成像方法[J].西安电子科技大学学报:自然科学版,2014,41(4):1-5.
YANG Ke,LIAO Guisheng,XU Qing. Research on interfere ometric imaging for rotor synthetic aperture radar[J]. Journal of Xidian University:Natural Science,2014,41(4):1-5.(in Chinese)
[2]Simeunovic M,Djurovic I,Djukanovic S.A novel refinement technique for 2-D PPS parameter estimation[J].Signal Processing,2014,94:251-254.
[3]Candès E J,Romberg J,Tao T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].Information Theory IEEE Transactions on,2006,52(2):489-509.
[4]ZHENG J,SU T,LIU Q H,et al. Fast parameter estimation algorithm for cubic phase signal based on quantifying effects of Doppler frequency shift[J].Progress in Electromagnetics Research,2013,142:57-74.
[5]Djurovic I,Simeunovic M,Djukanovic S,et al. A hybrid CPF-HAF estimation of polynomial-phase signals:Detailed statistical analysis[J].Signal Processing,IEEE Transactions on,2012,60(10):5010-5023.
[6]O'Shea P.On refining polynomial phase signal parameter estimates[J].Aerospace and Electronic Systems,IEEE Transactions on,2010,46(3):978-987.
[7]杜小丹,周良臣,杜雨洺,等.多相式相位信号参数估计新方法[J].计算机应用研究,2010(7):2502-2504.
DU Xiaodan,ZHOU Liangchen,DU Yuming,et al.New approach of polynomial phase signal parameter estimation[J].Application Research of Computers,2010(7):2502-2504.(in Chinese)
[8]光琳,宗序平.Logistic 模型的统计诊断[J].江南大学学报:自然科学版,2012,11(1):113-117.
GUANG Lin,ZONG Xuping. Statistical diagnosis of logistic model[J]. Journal of Southern Yangtze University:Natural Science Edition,2012,11(1):113-117.(in Chinese)
[9]宋玉娥,陶然,时鹏飞,等.基于LCT 域模糊函数的QFM 信号参数估计算法性能分析[J]. 北京理工大学学报,2014,34(9):940-943.
SONG Yue,TAO Ran,SHI Pengfei,et al.Performance analysis of parameter estimation algorithm for QFM signals using ambiguity function the linear canonical transform domain[J]. Transactions of Beijing Institute of Technology,2014,34(9):940-943. (in Chinese)

