基于过程神经网络的储层微观孔隙结构类型预测

张 强 许少华 富 宇

(东北石油大学计算机与信息技术学院，黑龙江 大庆 163318)

石油储层的微观孔隙结构是影响储层流体储集能力和石油开采的主要因素[1]，正确识别其类型是提高储层产能和油井采收率的关键。储层微观孔隙结构识别主要有室内实验法(扫描电镜法、铸体薄片法、毛管压力曲线法和CT扫描法)和测井资料评价法[2,3]，且主要局限于室内实验，实验方法价格昂贵，多偏重于理论研究，对于在井场上大范围应用还存在一定的局限性。测井曲线资料能连续从平面和纵向反映地层性质，可以等价成与时间有关的连续数据，资料全面且获取容易。笔者利用过程神经网络[4]预测孔隙结构类型，寻求测井信息与微观孔隙结构类型之间的一种非线性映射，通过改进的混合文化蛙跳算法和给定的学习样本集训练网络模型，并对未知样本进行孔隙结构类型预测，取得了很好的应用效果，为研究储层岩石孔隙结构特征开辟了一条新的途径。

1 基于双层过程神经网络的储层微观孔隙结构预测模型①

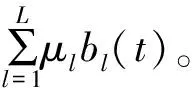
图1 双层过程神经网络预测模型

由图1推导输入层与输出层的关系为：

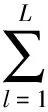
(1)

将xi(t)、wij(t)在给定精度下用b1(t),b2(t),…,bL(t)基函数展开，则网络输入输出之间的变换关系可表示为：

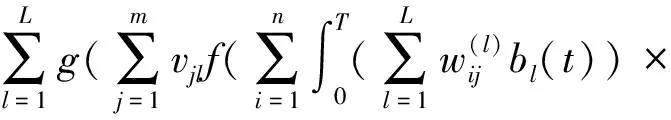
(2)

整理得：

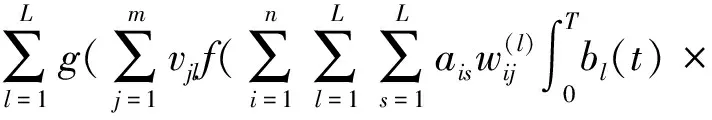
(3)

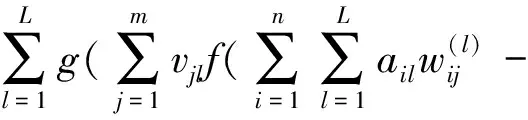
(4)

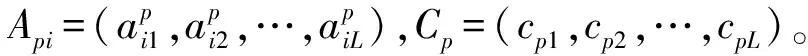
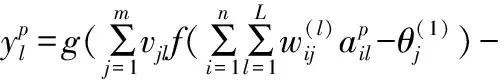
网络误差函数定义为：

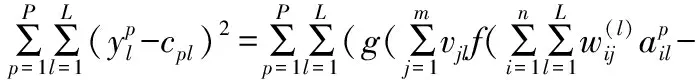
(5)

2 过程神经网络学习算法

2.1 混合文化蛙跳算法(MCSFLA)

过程神经网络的BP学习算法需要计算复杂的梯度信息且对初值敏感[5]，而混合蛙跳算法(SFLA)[6]具有实现简单及寻优能力强等优势，文献[7～9]证明其在求解某些问题时优于一些进化算法，但其在求解高维连续优化问题时效果不够理想。笔者将文化算法[10]引入到经典蛙跳算法中，提出一种混合文化蛙跳算法训练网络模型，即用改进的蛙跳算法来进化群体空间，用云模型作为信念空间的进化方式，完成知识经验的形成、存储和传播，有效克服了BP算法存在的问题。

2.2 群体空间的进化方式

群体空间的进化操作采用混合蛙跳算法来完成，但其进化机理使其在求解高维连续优化问题时效果不够理想，主要是因为最差解更新时，先参考子群内的最优个体，若不能提高则再参考全局最优个体，这种方式使得获取到的信息过于单一，没有同时考虑这两个最优个体对最差个体的影响，导致算法在处理大规模复杂问题时容易陷入局部最优，笔者依据最优觅食理论对其进行改进，动物在觅食行为过程中总是趋向于耗费更低的能量而获得更多的食物，以达到能效最好[11，12]。计算某一个体受到的能效吸引力的公式如下：

(6)

式中djk——个体xj、xk之间的距离；

f(x)——适应度函数；

Fjk——能效吸引力。

这里仅考虑Fjk≥0的情况，设对更新个体产生最大能效作用力的个体所处的位置为xnx，为了丰富个体的参考信息，改进经典算法的个体更新方式，在更新位置时同时参考子群内最优个体xb、全局最优个体xg和xnx，如果都不能改进则采用混沌映射重新产生新个体。新的位置为：

(7)

式中rand()——[0,1]的随机数；

w——吸引系数。

2.3 信念空间的进化方式

信念空间的个体来自于群体空间的最优子集。社会学原理指出优秀个体附近往往存在着更优个体，在其附近更有机会发现最优值。故为了能让信念空间更好地指导群体空间，需要在信念空间中发掘更多的优秀个体，笔者利用云模型来改变原有个体的进化方式。云模型是一种定性概念与定量数值转换的不确定转换模型，具有不确定性中伴有确定性、稳定中存在变化的特点，能表征自然界中物种进化的基本原理[13～15]，采用期望Ex、熵En和超熵He来表示。Ex表示最能代表定性概念的值，是新个体产生的中心，故将空间内的每个个体作为Ex；En表示定性概念的不确定性程度，反映随机性与模糊性之间的关联，体现优化空间中解的搜索范围，故将当代适应度方差σ2作为En动态改变搜索范围；He是熵的度量，反映了在论域空间代表该语言值的所有点的不确定度的凝聚性，它由熵的随机性和模糊性共同决定，将En/5作为He，初期加大算法的随机性，后期加强算法的稳定性。将信念空间的个体看作一个云滴C(Ex，En，He)，用它们产生与空间数量相同的一组云滴，如果新解优于原来个体则用其替换，实现方法如下：

a. 产生一个以En为期望值、He为标准差的正态随机数En′；

b. 产生一个以Ex为期望值、En′的绝对值为标准差的正态随机数X；

d. 重复步骤a、b直到产生n个云滴为止。

2.4 接受函数的实现原理

利用接受函数将群体空间的一组最优子集传递给信念空间。由于经典蛙跳算法各子群每一次迭代都会对个体适应度进行排序，所以对于每一个子群设置一个选择比例α，按这个比例取每个子群中前几个最优个体来传递个体经验，由各个子群提供的优秀个体和信念空间的个体采取锦标赛法来更新信念空间的个体。考虑到不同迭代次数中蛙群每个子群的个体对信念空间的贡献不一定都是一致的，所以每个分组选取的比例也应该不同，适应度好和子群多样性好的分组应该比例高一些。设蛙跳算法共分为N组子群，X(t)=(x1(t),x2(t),…,xN(t))是第t代每个分组的最优位置，以求最小值为例，当代N个分组中最好的适应值fbest(X(t))=min{f(xi(t))|i=1,2,…,N}，当代N个分组中最差的适应值fworst(X(t))=max{f(xi(t))|i=1,2,…,N},N个分组中适应度的方差为E(t)=(e1(t),e2(t),…,eN(t))，计算每个分组的选择比例：

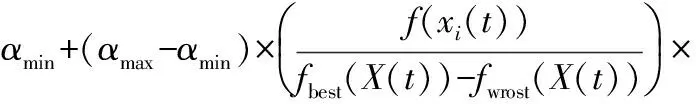
其中，αmax、αmin为取值比例区间的最大值和最小值。公式对适应度值越大、方差越大的值取较大值，表明对于适应度好、分组内适应值离散程度大的蛙跳分组提供相对较多的个体经验。

2.5 影响函数的实现原理

信任空间的影响函数为：

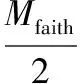
(8)

式中Mfaith——信念空间内的个体数；

t——当前迭代次数；

T——算法的总迭代次数。

在信念空间中选取前NUMfaith个优秀个体更新群体空间中的最差个体。

3 实验仿真

3.1 函数极值优化

函数1

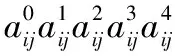
该函数全局最大值是1.002，求解结果大于1时停止求解。

函数2

该函数全局最大值是1，当求解结果大于0.995时停止求解。

分别对f1、f2采用GA、PSO、SFLA、MCSFLA4种算法求解50次，种群规模均设为50，算法求解的迭代次数设为100，MCSFLA、SFLA分组方式为m=5,n=10，PSO的惯性因子ω=0.5，自身因子c1=2，全局因子c2=2，变异概率pm=0.08，GA的交叉概率pc∈(0.6，0.8)，其变异概率pm∈(0.01，0.08)，优化结果对比见表1。

表1 函数极值优化结果对比

3.2 预测模型测井参数优选

描述储层微观孔隙结构的参数很多，选取自然电位、自然伽马、浅侧向、微梯度、微电位及深侧向等8条与储层微观孔隙结构有关的测井数据作为此处过程神经网络识别模型的输入，孔隙结构类型(1、2、3、4、5)作为网络输出，最后利用预测区块的取芯数据通过物理方法研究验证模型的正确性,图2为某油井2 200～2 400m的部分测井数据曲线。

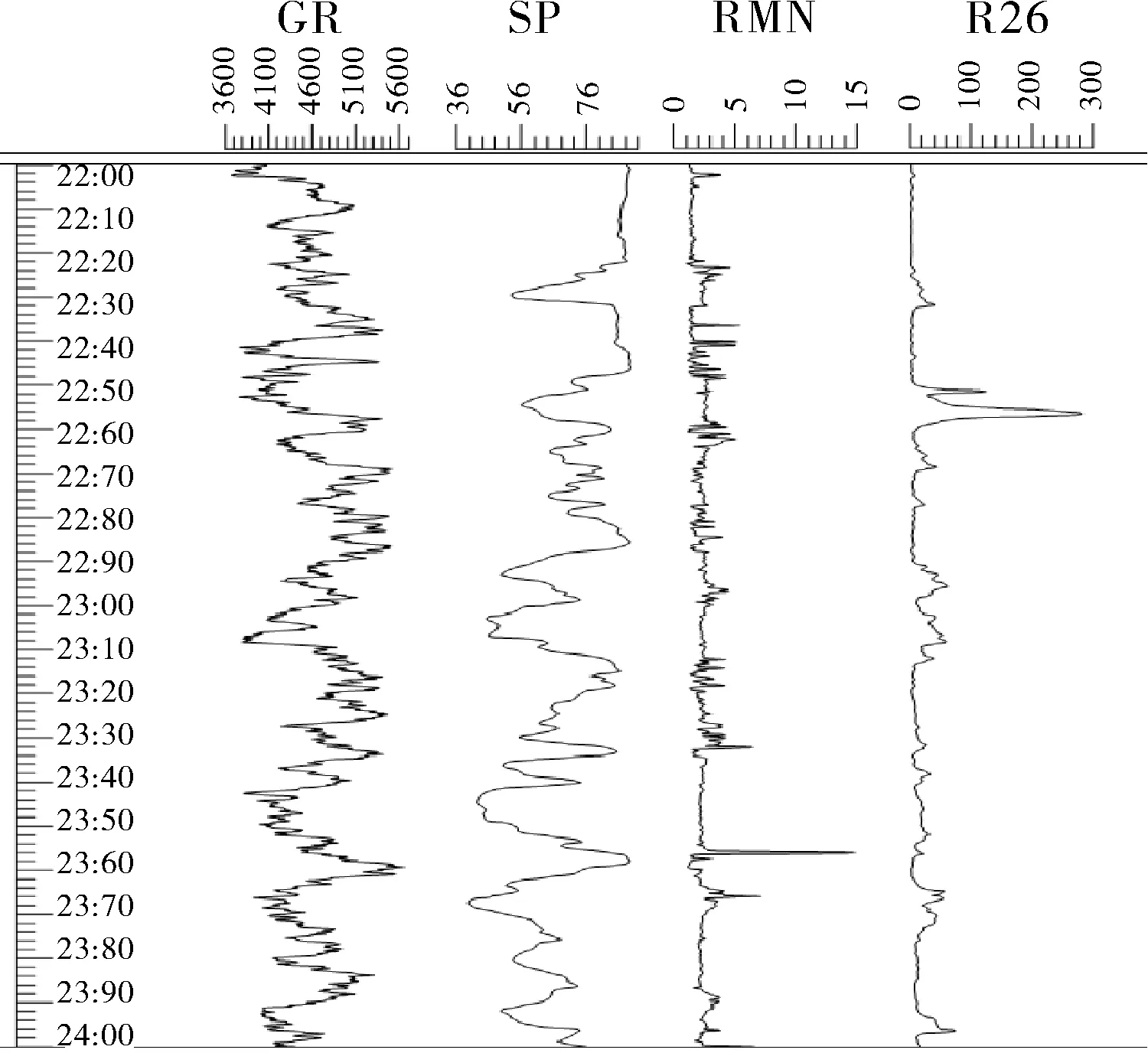
图2 部分测井数据曲线

3.3 储层微观孔隙结构类型预测

采用160个测井数据样本组成训练样本集，40个测井数据样本组成测试样本集，比较BP算法(BP-PNN)、粒子群算法(PSO-PNN)、经典蛙跳算法(SFLA-PNN)和笔者算法(MCSFLA-PNN)优化的预测效果。网络识别模型结构设置为8-16-L-1，选择Walsh函数作为基函数，基函数展开项系数L=16；学习算法误差ε=0.5；网络训练学习最大次数M=10000；各种训练算法独立优化10次。各算法的结果见表2。利用学习后的网络识别模型对训练样本集和测试样本集进行判别，判别结果见表3。

从识别网络模型的学习时间和判别结果可以得知，BP-PNN效果最差，PSO-PNN和SFLA-PNN次之，MCSFLA-PNN最好，分析其主要原因是BP算法要计算大量的梯度信息，算法本身的早熟等问题对提供准确判别也存在一定的影响，MCSFLA-PNN较快，分析其原因是由于MCSFLA在迭代时只更新最差粒子，最好情况下一次迭代只计算一次，最坏情况才计算4次，相对于粒子群每次迭代更新所有粒子计算量要少，云模型的稳定倾向性可以较好地保护最优个体从而实现对周围更优个体的靠近，有利于提升算法的优化速度和计算效率，并且混沌理论的突变作用可以较好地避免算法在迭代后期陷入局部最优，有利于在整个解空间找到最优解。

表2 学习算法结果对比

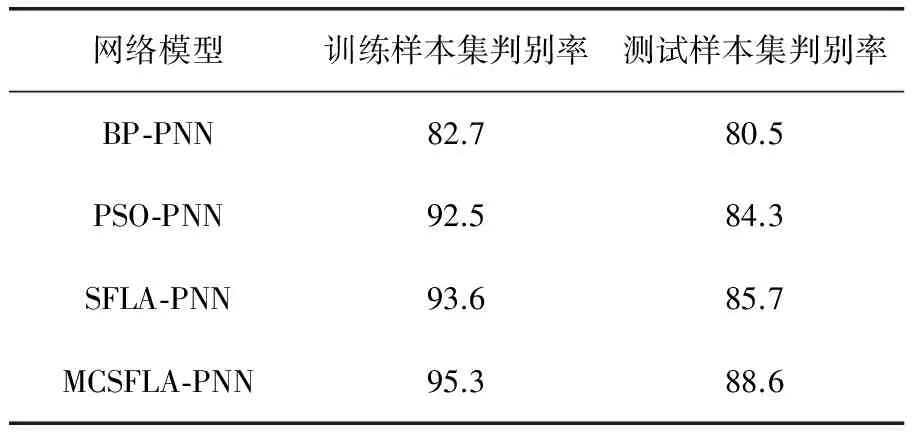
表3 判别结果对比 %

4 结束语

将测井曲线作为双层过程神经网络模型的输入数据来预测储层微观孔隙结构类别，采用提出的混合文化蛙跳算法来训练模型，实验仿真结果表明此方法具有很好预测结果。将已有实际测井数据和智能计算理论相结合应用到油田的开采过程中，具有投入少效益高的优势，通过储层孔隙结构的有效识别进而辅助油田工作者制定提高油井采收率的方案，以期最终提升石油开发的经济效益。

[1] 杨正明,姜汉桥,李树铁,等.低渗气藏微观孔隙结构特征参数研究——以苏里格和迪那低渗气藏为例[J].石油天然气学报,2007,29(6):108～110,119,172.

[2] 聂晶.应用测井资料分析微孔隙结构的方法研究[D].大庆:大庆石油学院，2009.

[3] 郝乐伟,王琪,唐俊，等.储层岩石微观孔隙结构研究方法与理论综述[J].岩性油气藏,2013,25(5):123～128.

[4] 何新贵,许少华.过程神经元网络[M].北京：科学出版社,2007.

[5] 钟诗胜,朴树学,丁刚.改进BP算法在过程神经网络中的应用[J].哈尔滨工业大学学报,2006,38(6):840～842.

[6] Eusuff M M,Lansey K E.Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm[J].Journal of Water Sources Planning and Management,2003,129(3):210～225.

[7] Elbeltagi E,Hegazy T,Grierson D.Comparison among Five Evolutionary-based Optimization Algorithms[J].Advanced Engineering Informatics,2005,19(1):43～53.

[8] Amiri B, Fathian M, Maroosi A.Application of Shuffled Frog-leaping Algorithm on Clustering[J].International Journal of Advanced Manufacturing Technology,2009,45(1-2):199～209.

[9] Rahimi-Vahed A,Mirzaei A H.A Hybrid Multi-objective Shuffled Frog-leaping Algorithm for a Mixed-model Assembly Line Sequencing Problem[J].Computers and Industrial Engineering,2007,53(4):642～666.

[10] Reynolds R G.An Introduction to Cultural Algorithms[C].Proceeding of the 3rd Annual Conference on Evolutionary Programming. San Diego,RiverEdge,NJ:World Scientific Publishing Co,Inc,1994:131～139.

[11] 孙儒泳．动物生态学原理[M].北京：北京师范大学出版社，2001.

[12] 崔志华，曾建潮．微粒群优化算法[M].北京：科学出版社，2011.

[13] 付斌,李道国,王慕快.云模型研究的回顾与展望[J].计算机应用研究,2011,28(2):420～426.

[14] 张光卫,何锐,刘禹，等．基于云模型的进化算法[J]．计算机学报，2008，31(7):1082～1091.

[15] 张英杰，邵岁锋，Julius N.一种基于云模型的云变异粒子群算法[J]．模式识别与人工智能，2011，24(1):90～96.