“原型—模型”,数学学习的原创过程
杜海良
教学内容:
苏教版数学五年级下册第93—95页。
教材分析:
本课“圆”是学生小学阶段学习的最后一种平面图形,也是学习的唯一一种平面曲线图形。圆被人们认为是一个美观又充满神秘的图形,是一个看似简单,实际上却很奇妙的形状。早在战国时期,我国古代伟大的思想家墨子,就已经为圆下了一个定义:“圆,一中同长也。”用今天的话说就是:平面上到定点的距离等于定长的所有点组成的图形叫作圆。这是圆与学生之前已经学过的其他平面图形最本质的区别特征。
《圆的认识》一课,在很多公开课场合都能听到,主要围绕圆的特征和画圆来展开。很多课上下来,学生也能顺利认识圆、掌握圆的特征,但对于圆“一中同长”这一本质特征的认识可能还是有欠缺的,如“圆中心的一点叫圆心”“连接圆心到圆上任意一点的线段是半径”“同一个圆里有无数条半径”“这无数条半径都相等”这些概念学生可能能正确记忆,但是不一定清楚这些特征的“来源”。正因为“圆是平面上到定点的距离等于定长的所有点组成的图形”,所以这一“定点”其实就是圆心,“距离”就是半径的长度,“所有点”就说明有无数条半径,“定长”就说明这无数条半径都相等。
所以本课的关键,是让学生理解圆“一中同长”这一思想。有了这一思想,圆的特征,包括画圆的原理、方法学生就能很轻松地获得,并在此过程中体会到数学的神奇与奥秘,激发数学学习更大的热情。但是,“一中同长”这一思想,对于学生来说比较抽象,认识起来比较困难,能不能从学生的生活经验中找到原型呢?本课的教学设计,就是试图从学生的生活中找到“一中同长”思想的原型并显性化,帮助学生深刻认识、掌握圆的特征和画圆的原理与方法。
教学目标:
1.初步掌握圆的特征,会用圆规画圆。体验数学与日常生活密切相关,能用圆的知识来解释生活中的现象或用生活中的现象来解释圆的特征。
2.通过观察、猜测、操作、交流等活动,培养学生的动手操作能力和抽象、概括、归纳等思维能力。
教学重点:
理解和掌握圆的特征“一中同长”,学会用圆规画圆。
教学过程:
一、创设情境,初步认识特征
1.创设情境
师:六一儿童节快到了,学校举行投球比赛,同学们围成这样的队形向球筐中投球,比谁投中的次数多,你认为这个比赛公平吗?
生:不公平,因为每个人离球筐的距离不相等。
师:那围成正方形的队伍呢?
生:不行。
师:那要围成怎样的队伍,你认为才公平?
生:圆形队伍。
师:是这样吗?
生:不是。
2.认识圆心
师:球筐应该放在什么位置?
生:球筐应该放在圆的中心。
师:那要怎样才能找到这个圆形的中心呢?请大家拿出老师为大家准备的圆片来模拟找出这个圆的中心。
生:汇报交流。
师:大家找出的这个中心就是圆的圆心,通常用字母“O”(板书)表示。请你在自己的圆片上点上圆心,标上字母“O”。
3.认识半径
(1)讨论。
师:球筐应该放在圆心位置,为什么这样比赛就公平了?
生:每位同学离球筐的距离都相等。
师:那也就是说圆上的每一点到圆心的距离都相等,我们也可以说成是:到一个中心距离都相等的所有的点组成了圆形,用我国古代思想家墨子的话说就是:“圆,一中同长也!”
(2)意义。
老师画出一条连接圆心到圆上任意一点的线段,像这样的线段就叫作圆的半径。(板书:半径)半径用字母“r”表示。(板书:r)
谁再来说说什么叫半径?
(3)特征。
请你也在刚才的圆片上画出一条半径,标上字母“r”。这样的半径你还能再画吗?能再画多少条?这无数条半径长度都相等吗?你能结合投球比赛的经验加以说明吗?
4.小结
通过刚才的学习,我们知道了在同一个圆内半径都相等这一道理,所以把球筐放在圆心位置时,比赛就公平了。
评析:以上教学是本课概念形成的关键步骤。圆心、半径这两个新概念都是在“投球比赛”这一实际问题情景中自然流畅地解决的。比赛时,球筐位置就是圆心,同学们到球筐的距离就是半径的长度。为了保证比赛的公平,学生都清楚每个同学到球筐的距离要相等,也就是半径都相等。通过“怎样的投球比赛才公平”这一生活原型,从中抽取出“一中同长”这一圆的本质特征,使学生对圆的认识产生了由生活原型到数学模型的飞跃。这样,本课的教学难点就比较自然、流畅地突破了。
二、对比辨析,进一步认识特征
1.揭示直径
师:(在黑板上的圆中直接画出直径)这条线段是半径吗?
生:不是。
师:对,这条线段不是半径,这是直径。(板书:直径)直径用字母“d”表示。
2.判断直径
请你凭着这条直径给你的信息,判断图中哪一条线段是直径,其他的为什么不是?
3.意义特征
(1)猜测。
根据上面的学习,你能猜一猜什么样的线段叫直径了吗?直径又有些什么特征?它与半径又有什么关系?
(2)验证。
请大家利用手中的圆片量一量、折一折,验证你的猜想。
评析:直径的概念可以说是半径概念的简单衍生,同一直线上的两条半径就组成一条直径,所以在半径概念的基础上,直径的教学可以简单化,开门见山地告诉学生,这条线段不是半径而是直径,重点放在半径与直径的关系上。
4.练习巩固
⑴判断。endprint
①从圆心到圆上任意一点的距离都等于半径的长度。
②直径的两个端点在圆上,那么两个端点在圆上的线段就一定是直径。
③所有的半径都相等,所有的直径都相等。
④半径为3厘米的圆比直径为5厘米的圆要小。
⑤在一个圆里,直径最长。
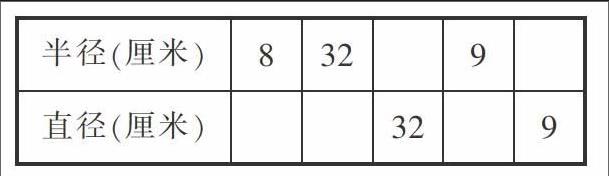
(2)填表。
三、应用特征,教学画圆方法
1.圆规画圆
师:根据“一中同长”的思想,科学家们设计了一种画圆的工具——圆规,你知道圆规为什么可以画圆吗?
师:请你试着在这张纸上画一个大小合适的圆,并说一说画时要注意什么?
生:画时不能改变针尖一脚的位置(定点——一中),不能改变两脚之间的距离(定长——同长)。
2.其他工具
师:如果没有圆规,你还有其他办法画圆吗?
师:古代的人们在生活劳动中也经常需要画圆,你知道他们是如何在地上画一个半径是5米的圆的吗?
动画演示用“绳子画圆”,并说一说这样画圆的原理。
评析:画圆的原理仍是依据“一中同长”的思想,所以画圆的教学仍然紧扣这一点。先探究为什么用圆规可以画圆,画圆时为什么要注意定点、定长,再思考还有什么其他方法也可以画圆,如用绳子画圆。这样的教学既能与前面的特征教学一脉相承,始终围绕“一中同长”的思想,并且也通过对画圆原理、方法的探究,进一步巩固“一中同长”的思想。
四、联系生活,实践应用特征
1.问题
生活中有许多圆形物体,有些物体做成圆形是为了美,而有些物体却是非圆不可,比如说车轮。车轮能不能做成方形或椭圆形的,为什么呢?
2.讨论
请同学们先相互讨论一下,然后再相互议一议。
3.演示
观看三种车轮的动画演示,结合“一中同长”的思想理解车轮为什么一定要做成圆形。
五、总结揭题
1.揭题
师:这节课我们学习了什么内容?
生:认识了圆。(板书:圆的认识)
2.总结
师:通过这节课的学习,你有哪些收获?
基于怎样让数学课堂再厚重些、开阔些、深邃些、美丽些的思考,有了“圆的认识”这一课,从“原型”到“模型”的尝试。基于原型的教学突出反映了数学本身产生与发展的动力特征,强调从数学自身发生、发展的角度思考情境的创设——以原型为核心的情境创设。在数学学习中创设以原型为核心的情境,可以激发学生的学习热情,使情境的挑战性、趣味性或应用性成为学习的动力;可以促进数学理解,使情境本身的信息为数学问题的解决、模型的建立提供结构性支撑。从“原型”到“模型”的学习,正是数学的原创过程在教学中的体现,这不仅有利于学生体会数学,逐步培养学生的创新精神和实践能力,同时也是一种人类的文化。?筻endprint

