丰厚预设，夯实课堂底蕴

王瑶洁

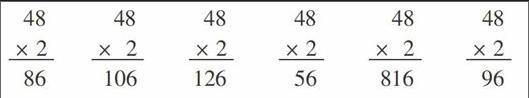
“凡事预则立，不预则废。”课堂预设可以说是教师对课堂教学的规划、设计、预设和安排，既包含教师对教材、学生的理解，更体现教师个人的教学理念和教学风格。教师只有课前进行充分的预设，才能在课堂上临危不乱，“运筹帷幄之中，决胜千里之外”。

如果我们把课堂教学看做一个充满张力的生命过程，那么预设既是课堂教学的孕伏过程，又是课堂教学的基石和源泉。课堂教学的好坏、效率的高低，与预设的有效与否直接相关。高效的课堂教学离不了精心的预设，只有课前进行充分的预设，才能成就精彩的课堂。

一、准确预设，为课堂教学奠定基石

常有人把课堂预设简单地等同于备课的教案，认为课堂预设是一种完全静态的、前置性的、单维的、主观的线性教学设计，而实际上，课堂预设是多维的、丰富的、开放的、动态的板块型设计。因此，教师要深入挖掘教材的编写意图，了解学生的学习心理和认知基础，分析教学中可能出现的各种问题，设计与之相应的应对策略、引导方式，合理设计教学的层次、环节和流程。

1.深挖教材，预设课堂教学基调

课堂教学前，教师要先深入研读教材，才能准确把握教学内容的重、难点，明确“教会学生什么”“哪些知识该教”“教到什么程度”等问题，真正明白是“用教材教”而不是“教教材”的道理。

例如，苏教版小学数学五年级下册第四单元“分数的认识”一课，早在三年级上册学生就第一次接触了分数，然后在三年级下册又再次学习了分数，到这里已经是第三次认识分数了，那这次让学生学习分数与以往有什么不同呢？该怎样教学更恰当呢？三年级上册第一次认识分数，主要是让学生体会把某件物品或某个图形平均分时会产生一类新的数，这里更多的是从感性认识的角度出发，结合生活实例和学生已有的知识基础、生活经验，通过丰富的操作活动，让学生亲身体验分数产生的过程;三年级下册第二次认识分数，主要是借助对图形的观察，引导学生通过动手操作，认识、理解一个整体的几分之一;五年级下册第三次认识分数，则是使学生能正确认识单位“1”，理解分数的意义，并能对具体情境中分数的意义做出解释，有条理地运用分数知识对生活中的问题进行分析与思考。因此，在课堂预设时，我设计以下四个板块：（1）说说对分数的了解，以旧引新;（2）合作探究，建立单位“1”的概念;（3）对比探究，系统理解分数单位;（4）练习比较，深化分数的意义。其中，主要聚焦第（2）、第（3）两个板块，即如何建立单位“1”的概念和理解分数单位。因此，教师一定要联系整套教材的内容，分析教材每次安排“分数的认识”的意图，从而吃透教材，准确把握教学。

2.顺应学生，预设课堂教学流程

作为一线教师，教学如果只盯着学生计算的正确率、从“本”到“本”的话，学生学到的就是有限的知识，而不可能获得灵动的、长远的思想方法。卢梭曾说过：“教育必须顺其天性而为。”因此，课堂教学中，教师应该立足学生的心理特点和认知基础，顺应学生的发展趋势和要求，设置适合学生需求的教学环节。

例如，我校华晴老师执教苏教版小学数学六年级“百分数的认识”一课时，设计“学校需要选一位体育老师参加投篮比赛”的问题来展开教学。首先，华老师提供两位体育老师的训练情况（投篮总个数和投中个数），让学生理解选择标准实际上就是比较投中个数占投篮总个数的分率，并明白在总个数不同的情况下可以通过通分来帮助比较;其次，随着参加训练的老师人数的逐渐增加、投篮总个数的不断变化，学生经历了一次又一次的通分去比较分数的大小。在这个过程中，学生体会到通分的种种不便，且费时、费力，实在麻烦，而随着华老师的一句话“参加训练的人数还在增加”，使学生真正感受到建立一个便于统一的比较标准是多么的重要，百分数由此应运而生。这样基于学生实际需求的课堂预设，让学生逐步感受到百分数产生的同时，深切体会到了百分数应用的价值，逐步建构属于自己的数学知识。

二、灵活预设，为课堂教学保驾护航

课堂教学中，学生的学情是随时变化的，教师的教学灵感是随时出现的，只要有利于课堂教学效率的提高，教师就应在吃透教学大纲、文本及掌握学生的实际情况下，灵活预设和调整课堂教学。

1.多维预设，明确课堂教学走向

多维预设，是指预设面对同一问题时，可能会出现多种不同思路的选择和优化。教师对教学要有充分的准备，以便面对学生不同的思维能及时做出正确的反应和合理的引导。

例如，在“两位数乘一位数”教学中，教师往往觉得这部分内容不是很难，常常把精力较多地放在引导学生理解算法上，从而忽略学生计算法则、算理的形成过程。但学生的思维是不是和我们预想的那样呢？为什么有的学生的计算正确率不高呢？我不禁反思：在没有正式教学之前，学生是怎么想的？他们可能会出现哪些情况呢？于是，我课前用48×2这一道题对学生进行了简单的调查，结果如下。

48         48         48         48          48         48

× 2        ×  2         × 2         × 2         ×  2         × 2

86          106        126         56         816         96endprint

出乎我的预料，学生对这道题的计算竟出现了六种解法！分析每种解法，我从中看到学生思维的过程和产生错误的原因：第一种解法没有进位;第二种解法把进位的数一起再乘了一遍;第三种解法把进位的1和乘数2先相加再去乘十位上的4;第四种解法进位后没有再乘;第五种解法把进位的1直接放在了十位上，再把十位乘得的数写在百位上;第六种解法才是正确的。因此，在实际教学中，我对课前调查时出现的各种情况预设了三个方面的应对：首先，引导学生对所有的解法进行比较，寻找其中的异同点;然后，对重点问题进行分析;最后，解决问题，达成共识。如：“看一看、想一想，你认为这些计算结果中哪些是正确的？问题出在哪里？”“那我们就重点来研究十位上的数吧！你看懂了谁的算法？在他的解法中，对十位上的计算是怎么想的？”“谁先来介绍一下自己的算法？”“看来，都是这个进位1在作怪啊！那我们在计算时要特别注意进位的处理。”……在实际教学中，学生果然出现了几种类似的算法，根据我的预设，引导他们在比较中逐层深入探究，学生自然而然地就把问题聚焦到计算的重点和难点——十位上来。这样教学，既让学生找到了问题所在，保护了他们稚嫩的自尊心，又引导学生找到了各种错误的原因，使他们明晰了算理，深切地感受到计算时每一个细节的重要性。

2.弹性预设，预留课堂教学空间

教育家布卢姆说过：“人们无法预料教学所产生的成果的全部范围。没有预料不到的成果，教学也就不成为一种艺术了。”无论课前预设得多么完美，在面对课堂上鲜活的个体——学生时，总有意料之外的“特例”。弹性预设就是指对教学过程多做一些假设，给学生留有更大的包容度和自由度，为学生预设充分的发展空间。

例如，教学“3的倍数的特征”一课的巩固练习时，教师可预设以下三个环节：第一个环节，简单应用，巩固认识;第二个环节，灵活运用，形成策略;第三个环节，综合运用，形成技巧。由于学生已经有了探究2.5的倍数的特征的知识储备，在探索3的倍数的特征过程中也积累了“各个数位上的数是3的倍数，和也是3的倍数”的事实经验，学生有可能主动跳出课前的第一个环节预设（巩固认识）和第二个环节预设（形成策略），而直接进入第三个环节预设（形成技巧）。这时教师可以灵活地将三个环节的学习活动进行整合，主动让学生到台前作“主角”，通过质疑和交流，使不同层次的学生互相学习、互相补充，获得不同的发展。

预设是高效课堂的前提和基础。作为教师，既要注意从教材、学生、自己的教学思想和方法上努力提高预设的水平，又要提高自己的教学应变能力，培养教学机智，收获预设之外的精彩！

（责编 蓝 天）endprint