给学生一个辩解错误的机会

赵彦

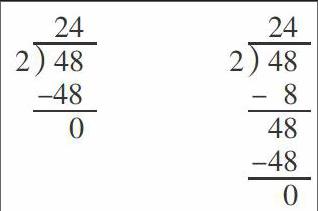
案例回放：

教学“竖式除法计算”一课时，我以为很简单的一个知识点，学生学习应该很顺利，没想到在新授课上却发生了意外。在口算48÷2时，学生都能得到计算结果为24，但到了竖式计算的环节，学生却出现了错误。如下：

■

显然，这两种错误很离谱，也有些莫名其妙，我很快打了大大的红“×”号。可在批改作业时，发现仍有一部分学生犯同样的错误，这让我对学生的解题思路产生了好奇。于是，我认真询问了学生的想法。学生回答：第一个竖式，从个位算起，先看8除以2等于几，二四得八，8÷2=4，从48里边去掉8还剩40，40除以2等于20，十位上是2，这样就得到商是24;第二个竖式，先从个位算起，二四得八，8除以2等于4，从48中减去8还剩下40，40除以2等于20，刚好除尽，所以商为24。从学生的想法来看，显然是有道理的，可为什么要从个位开始进行除法计算呢？学生认为，以前学习竖式计算时，加法、减法、乘法都是先从低位算起的，那么除法应该也不例外。根据学生的这一算法，我觉得很有道理，但是否能够适用所有的竖式除法呢？于是，我追问：“如果被除数的个位不能被除数整除呢？你还能采用这样的方法来进行竖式计算吗？如45÷3，你怎么计算？”学生立刻写出答案，并说出了自己的想法：“因为个位上的5除以3除不尽，所以要从十位上借1，这样个位上的数变成了15，三五一五，15÷3=5;从45中去掉15剩下30，30除以3等于10，正好除尽，所以商是15。”

分析及对策：

上述学生的错误虽然从程序上不符合教材所要求的从高位入手进行竖式计算，但学生能够进行独立思考，将以往的数学经验顺利迁移到新知学习中，这足以说明学生具有合情推理的能力。那么，如何将这一合理思考顺利地迁移到从高位入手进行竖式计算这一思路上来呢？我认为，不管是从高位入手进行竖式计算，还是从低位入手进行竖式计算，由于学生的数学经验相对较少，所以他们无法进行独立的抽象思考。作为教师，如果只是强制性地给学生指令，告诉他们必须从高位入手进行竖式计算，那么势必导致学生被动接受知识，虽然也会收到效果，但不利于学生数学思维的发展。于是，我决定从学生已有的知识经验出发，运用对比，让学生直观体验，分析哪种计算方法更便捷、更优越。

我先让学生用从低位入手的方法计算72÷3，学生计算过程如下：先算2除以3，不够整除，所以要从十位退1，加上个位上的2就是12，12除以3，三四十二，12÷3=4;71减去12还剩下60，再计算60除以3，60除以3等于20，正好除尽，所以商就是24。我追问：“想一想，可以从低位入手算起，那么能不能从高位入手开始算呢？”学生经过思考后写出算式，并汇报计算过程：72÷3，十位上的7除以3商为2，二三得六，7减去6还剩下1，其实是10;10加上个位上的2就是12，再计算12除以3，三四十二，商为4，正好可以整除，最后的得数十位上为2，个位上为4，所以72÷3的结果为24。接下来，我让学生分析比较两种计算方法的思维过程，学生认为从高位算起简单便捷，从低位算起比较复杂。于是我让学生重新计算48÷3，经过讨论后，学生发现从高位算起直接快速，从低位入手更适合口算，而口算则不需要进行竖式计算。由此，学生明确了竖式计算要从高位算起的一般规律。

思考：

不可否认，教师教学中往往会遇到一些另类的学生，他们有时会运用独特且富有创造性的思维方法来解决问题，但往往因为和教材设定的范本有所不同而被教师忽略，甚至被教师定位为错误，画上红红的“×”号。面对错误，教师为何不给学生一个辩解的机会，从学生的辩解入手展开教学呢？其实，教学中类似的情形并不鲜见，这让我有了以下的思考。

1.积累错误资源，发展思维

课堂教学中，无论是学生的作业还是发言都会出现错误，而这些错误正是宝贵的教学资源。教育家奥加涅相曾经指出：“教师忽视解题过程，把习题作为评价知识和技能、技巧等的主要手段，忽略数学思维能力的培养和发展，这已经成为数学教育的顽疾。”《数学课程标准》中也指出：“教师应当引导学生充分呈现和暴露自己的思维过程，使学生在自主思考中获得抽象思维的发展和对数学概念的建构，提高数学能力。”学生的错误既是呈现和暴露思维过程的最佳途径，也是展开思维过程的资源所在。

2.辩明错误思维，顺势而导

如上述案例中，学生的错误都是因为从低位算起导致的。在小学数学知识体系中，整数范围内的笔算加法、减法、乘法都是从低位算起的，只有除法是从高位算起的。学生之所以会出现这样的错误，说明受到笔算加、减、乘竖式计算的负迁移影响，导致整数除法的经验出现断层。此时，教师就要给学生一个机会，让他们为自己的错误辩解，说明自己的解题思路，展现自己的整个思维过程。教师则可以顺藤摸瓜，顺着学生的思维因势而导，这样既能有的放矢地对学生进行针对性的教学，又能使学生得到不同的发展。

总之，给学生一个辩解错误的机会，将为课堂带来新的生机和活力！

（责编 杜 华）endprint