例谈“三象一作”教学模式的实施策略
顾丽英+++许光新
王名扬等教授在《论一种缘自认知心理学及教育研究的数学认知过程》一文中,提出了一种全新的教学模式——“三象一作”,即“数学现象、心智图像、数学抽象、操作阶段”。这是一种缘自认知心理学和教育研究,可以应用于小学数学教学的“数学认知过程”。它的提出对数学教育和教学具有理论指导意义且具可操作性。
在日常教学中,笔者试图以这一理论为依据,在课堂上有意识地启示、鼓励学生,或促使学生搜集数学现象、观察数学现象,再通过多种策略让数学现象成为学生心中生动的心像,最后,再通过层层抽象,完成知识建构。本文笔者就从数学的现象、心像、抽象等层面谈谈苏教版小学四年级“小数意义”的设计策略。
一、呈现数学现象,着力于小数形象的积累
数学是研究数学现象的科学,数学教学就是阐述并运用“数学现象规律”的科学。数学现象是数学形式化题材的生命之源,也是学生直观心智图像形成的客观背景。生活中存在的大量的数学现象是可以人为地创设出来的。小数是描述性的概念,因此教师在教学小数意义的时候,首先就要从小数意义的知识本身以及学生已有的认知水平出发,呈现有效的数学现象,引入小数意义。综观各种版本的教材,笔者发现:苏教版教材以元、角、分、米尺等数学现象引入小数概念;人教版教材仅以米尺这一数学现象引入小数;北师大版教材以元、角、分引入小数意义;青岛版教材以生活实例和正方形、正方体等数学现象引入小数意义……各种版本的教材都试图以一种有趣、直观、形象的数学现象来生动引入小数意义。综合各个版本的教材,我们在呈现小数意义的数学现象时,应紧扣趣味性、直观性、连续性等特性,帮助学生积累小数形象。
1.生动有趣地引入数学现象
著名数学家华罗庚说过:“人们对数学早就产生了枯燥乏味、神秘、难懂的印象,原因之一便是脱离了实际。”因此,从学生熟悉的实际生活中创设教学情境,让数学走进生活,让学生在生活中看到数学现象,接触数学,激发学生学习数学的兴趣,就显得尤为重要。如上课一开始我们向学生呈现的是奥运冠军、中国男子田径队110米跨栏健将刘翔跨栏夺冠的场景,引导学生回顾历史上在跑步比赛中记录时间方法的发展史:用整数秒记录→用一位小数记录→用两位小数记录,为了比出胜负,记录的时间越来越精确。透过这一现象,学生可以真切地感受到小数是在精确度要求不断提高的情况下产生的。
2.数学形象的形成,需要丰富的数学现象作为资源
在学生初步感受到小数产生的必要性后,我们又设计了测量淘淘小朋友身高的数学情境,帮助学生搜索数学现象。首先呈现:测量小宝宝淘淘三个月大时的身高。从图片中,学生能清楚看到,测量结果不能用整米数表示,此刻启发学生利用已经学过的知识解决:缩小计量单位,把1米平均分成10份,每份是1分米,测得淘淘身高是6分米,也可以写成十分之六米或0.6米。这是学生在三年级时学过的知识。在这儿不仅复习了旧知,而且也使学生看到了一位小数出现的必要性,为后面的两位小数、三位小数的出现埋下伏笔(如图1)。
图1 淘淘三个月大时的身高
一位小数的出现已经比整数更加精确了,为什么还要出现两位小数呢?这时我们又呈现了这样的数学现象:淘淘六个月时,测量身高,图片显示用一位小数得不到精确的结果了,怎么办?学生非常自然地想到了用两位小数来表示,把1米平均分成100份,每份是1厘米,也就是一百分之一米,写成小数是0.01米,淘淘的身高67厘米就是0.67米(如图2)。
图2 淘淘六个月大时的身高
随着淘淘的长大,身高又发生了变化,于是,我们又呈现了第四个数学现象:七个月大时,淘淘的身高用两位小数无法精确地表示了,如此顺理成章地引出了三位小数(如图3)。
图3 淘淘七个月大时的身高
在这样层层递进的连续的数学现象中,我们可以看到一位小数、两位小数、三位小数的引出是那么的迫切与自然,因为在这一系列的数学现象中,不仅突出了小数产生的必要性,更重要的是蕴含了小数的内涵,在整个过程中学生积累了大量的小数现象,这为学生心智图像的形成奠定了基础。
二、激活心智图像,着力于小数内涵的丰富
“心智图像是数学现象在人们心目中呈现的一类未经理性分析的直觉形象,是人们对数学现象的某种直接的领悟和图像。”因为数学现象是对数学内涵的呈现,而心智图像是对数学现象的反映,所以我们称心智图像是对数学内涵的二次呈现。心智图像具有一定的概括性,由此也就有不同的迁移能力。数学学习中并非概括水平越高的心智图像越有利于数学理解。而是在不同的阶段,需要相应水平的心智图像。引导建构的心智图像必须能够反映数学本质,因为,不管形成怎样的心智图像,我们的目的都是为了帮助学生理解数学。小数是一个比较抽象的数学概念,为了帮助学生激活有效的心智图像,形成科学规范的小数意义的知识结构,我们在教学小数意义这一知识点时,预设形成以下直观、适切的心智图像。
第一,米尺是学生心中熟悉且形象的教具。学生曾经通过米尺认识了1米、1分米、1厘米、1毫米,并借助米尺了解了米、分米、厘米、毫米之间的关系。所以在教学小数意义时,通过把1米平均分成10份、100份、1000份,得到1米的十分之几、百分之几、千分之几,并用小数表示是1位小数、两位小数、三位小数等。此刻,学生心中会形成这样的心智图像:把1米平均分成10份,每一份是1分米,是1米的,用小数表示是0.1米;把1米平均分成100份,每一份是1厘米,是1米的,用小数表示是0.01米;把1米平均分成1000份,每一份是1毫米,是1米的,用小数表示是0.001米。这样米尺就在“米、米,米”和“0.1米、0.01米、0.001米”之间架起了知识桥梁,学生心中形成了从整数到分数到小数的相互贯通的心智图像。
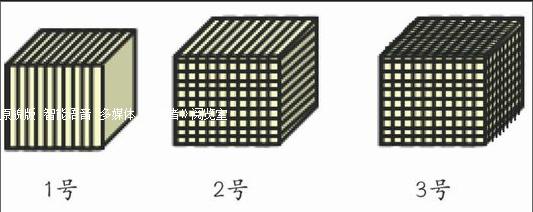
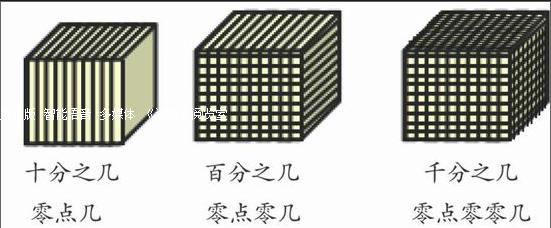
第二,我们可以用整数“1”来表示一个正方体。在这儿我们期望形成这样的心智图像:把正方体平均分成10份后,每一份是正方体的,可以用0.1来表示;把它平均分成100份,每一份是正方体的,可以用0.01表示;把它平均分成1000份,每一份是正方体的,可以用0.001表示。这儿把正方体从一维、二维到三维的直观均分,可以让学生心中顺利从“十分之几、百分之几、千分之几”过渡到“零点几、零点零几、零点零零几”,这一心智图像的形成,有助于学生沟通分数与小数之间的联系(如图4)。endprint
十分之几 百分之几 千分之几
零点几 零点零几 零点零零几
图4 剖分单位正方体理解小数意义
第三,数轴在小学教材中多次出现,是学生认数的重要工具。认识小数一课中,我们借助数轴,让学生心中形成这样的心智图像:把数轴上0到1这段平均分成100份,从0开始第二个点可以用表示,也可以用0.01表示;第三个点可以用表示,也可以用0.02表示……使学生明白数轴上的每一个点都可以用不同形式的数来表示,这样就由数轴这一中介沟通了整数、分数、小数之间的联系。
三、实现深度抽象,着力于小数本质的认识
人脑是具有抽象本能的。通过心像的积累、变化、组合及相互联结和综合等过程逐步形成抽象性的概念——小数的意义。因此,当学生形成了以上的数学心像后,需要教师引导他们通过对比、归纳、推理等完成小数意义的抽象。
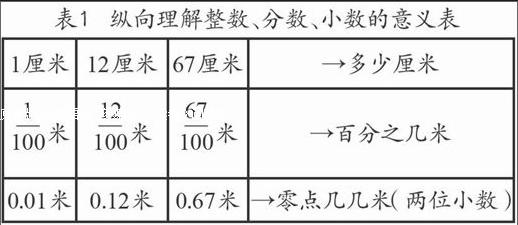
第一,横向比较、纵向感受小数的意义。当学生借助米尺在心中形成纵向的整数、分数与小数之间的联系后(如表1),教师及时地引导学生进行横向的求同比较,使学生明确,第一行都是表示多少厘米,第二行都是分母是100的分数,第三行都是两位小数,在此基础上引导学生进一步概括,多少厘米都可以借助分母是100的分数表示出来,还可以借助两位小数表示出来。在教学三位小数时同样可以采用类似的方法,让学生明确,多少毫米都可以借助分母是1000的分数表示出来,也可以借助三位小数表示出来。这就是从整数到分数到小数的一个纵向的小数意义的理解。
表1 纵向理解整数、分数、小数的意义表
1厘米 12厘米 67厘米 →多少厘米
米 米 米 →百分之几米
0.01米 0.12米 0.67米 →零点几几米(两位小数)
第二,分类归纳,逆向理解小数的意义。在这节课中如果仅仅让学生理解分母是10,100,1000……的分数都可以写成一位、两位、三位小数……是远远不够的。所以当学生认识了0.1,0.4,0.7,0.01,0.04,0.12,0.67,0.001,0.028,0.677等小数后,我们可以设计这样的一个环节:请学生选择下面的一个正方体来表示这些小数(如图5)。
1号 2号 3号
图5 逆向理解小数的意义
通过分类选择,我们可以得到0.1,0.4,0.7可在1号正方体中表示,0.01,0.04,0.12,0.67可在2号中正方体表示,剩下的在3号正方体中表示。这样数形结合着对应分类,学生非常自然地得出了小数意义的逆向理解:一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……此刻,我们可以说,学生对小数的意义已经可以比较完整地构建。
第三,推理猜想,感悟小数的特征。数轴是数的认识的重要工具。它的出现,不仅可以让学生对小数意义的认识更加深刻,而且可以使学生逐步感悟小数的特征。这里我们可以设计三个递进的推理猜想,让学生感受小数个数的无穷性。
其一,在数轴上,引导学生在0与1之间找到0.1,0.01,0.001的位置,通过直观位置的对比,让学生清晰地看到,这几个小数中最接近0的小数是0.001,并且在0与0.001之间,我们还可以找出比0.001更小的小数0.0001,在0和0.0001之间,还可以推想出0.00001,以此类推,学生很容易就可以推想出在0与1之间,我们可以找到无数个小数;同样,1和2之间、2和3之间也有无穷个小数。这样,通过观察与推想,学生可以知道在每两个整数之间都存在着无穷个小数。第一次感受小数个数的无穷性。
其二,将数轴的箭头向右继续延伸,从0到1到2到3,进而自然地引出π的近似值:3.1,3.14, 3.141,3.1415,3.14159,3.1415926……而3.141,3.1415,3.14159,3.1415926……这些数都在3.14和3.15之间,由刚才的推想,学生可以非常顺利地推想出3.1415926后面还可以有无限位小数,也就是说,在3.14和3.15之间,我们也可以推算出无限个小数,这时,学生就可以推想出每两个小数之间也有无穷个小数。
其三,数轴不断向右延伸,学生在数轴上依次找到15.8,25.7,100.9,358.9,8844.47……在数轴向右无限延伸的动态过程中,学生不仅看到了小数变得非常非常大,从而明白小数其实并不小,再加上学生合理的推想,又可以感受到小数可以是无穷大的特征。
通过这样三个层次的抽象概括,学生对小数的意义及特征逐渐明晰。
综上所述,运用“三象一作”的理论进行小数意义的教学,教师从呈现紧密相连的数学现象入手,使学生的心中形成科学规范的心智图像,通过多维度的比较、抽象、概括,使小数的概念清晰、丰厚,从而在学生心中架构一个完全“立体化”的小数意义。
(江苏省无锡市新区实验小学 214112)endprint

