流量同时作为工艺优化变量和串级控制副变量时的工艺优化实现与分析
罗雄麟 叶松涛 许 锋 张其方 刘雨波
(中国石油大学信息学院,北京 102249)
为了提高装置的经济效益,在实际操作过程中要求随产品价格及工况等的变化在线做出调整。在线优化是应用过程建模、优化技术、先进控制和计算机技术,在满足生产安全要求及产品质量约束等条件下,将最优工艺参数直接作为控制器的设定值,由控制系统不断计算并改变过程的操作条件,使得生产过程始终运行于最优状态[1~3]。串级控制是石油化工领域中广泛采用的一种底层控制系统,具有改善对象的动态特性、提高工作频率及抗干扰能力和自适应能力强等优点[4,5]。在串级控制中,副回路控制器的设定值由主回路控制器输出决定。因此,当副被控变量作为在线优化变量时,由于在线优化得到的优化结果不允许直接下载到串级控制副回路控制器中,其在线优化结果的实现存在问题。
这一问题在石油化工过程中的典型体现是流量优化变量在串级控制中的实现问题。流量作为重要的工业被控变量,在生产过程中通常受到频繁且幅度大的扰动,因此实际生产中广泛采用串级控制结构,通过构建流量控制副回路,将影响主被控变量最严重、频繁、激烈的干扰因素抑制在流量副回路中,从而改善整个系统的动态品质,确保主被控变量,如温度、液位及成分等的控制效果[6,7]。同时化工过程各单元设备中进行的流动、传质、传热等物理过程,以及反应器中存在的化学反应过程都与流量的变化紧密关联,流量又具有测量容易、与各项经济指标关联紧密的特点,因此,连续工业的在线优化通常选择流量作为优化变量[8~11]。面对广泛存在着的底层为流量副回路串级控制系统,在线优化得到的流量设定值不允许直接下载到串级控制副回路的流量控制器中,造成在线优化结果不可实现。所以对串级控制结构进行分析和改善,提出相应的在线优化实现方案,具有较大的现实意义。
笔者通过对串级控制进行分析,提出了几种串级控制在线优化实现结构,并针对其优缺点进行比较分析,最终选出一种简单通用的优化变量串级控制实现方法。通过增益变换,将副回路优化变量的实现转变成对主回路过程变量的优化,并通过增加惯性环节,在保障理想调节时间的条件下使超调量大幅减小,保证了优化实现的快速与平稳。该方案不改变现场串级控制结构,避免了对模型精度和控制参数要求苛刻的问题,其控制实现结构简单,并通过实验模拟有效地证明了控制方案的可行性。
1 在线优化的实现问题①
在正常情况下,工业过程各种参数是基本稳定的,但由于外界干扰及设备老化等原因,工业生产过程会偏离最优点。因此,需要采用在线优化技术以寻找到并维持工业过程的最优工况,提高经济效益。如图1所示,面对广泛存在的底层串级控制系统,当副被控变量作为优化变量时,由于在线优化得到的优化结果无法直接下载到串级控制副回路控制器中,其在线优化结果的实现存在问题。
以温度流量串级控制为例说明,若将优化得到的流量设定值直接下载到副回路的PID控制器中,因为副回路PID控制器的设定值Fsp是通过主回路的控制器得到的,如果Tsp不变,经过几个控制周期后,副回路的流量设定值仍然会回归到Fsp,而不是固定在优化得到的Fop。而若将主控制器Gc1断开,让副回路独立工作,优化得到的流量值Fop就可以直接送给副回路的控制器作为设定值,主控制器的设定值可以变换为Optimizer优化模型中的不等式约束,不等式约束为Tsp-ΔT≤T≤Tsp+ΔT。这种方法虽然简单易行,但有很大的局限性,因为其改变了原来的控制结构,常为现场所不允许,如果工艺过程不允许串级控制打开,这种方法还是不能满足优化结果的实现。因此,需要寻找解决过程优化得到的流量值在串级控制中的实现方法。
2 在线优化的实现方案
由于优化得到的结果不允许直接送给副回路的控制器,只允许送给主回路的控制器,所以可以通过串级控制中的传递函数关系把应该下载到副回路流量控制器中的变量值转换为主回路控制器中的变量值,这需要知道串级控制中各个模块的传递函数,推导出Fsp到Tsp的传递函数关系,根据图1中的各个传递函数进行推导。
首先得到Tsp到Fsp的传递函数关系:
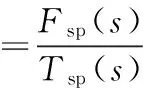
=Gc1(1+Gc2GvGp2Hm2)1+Gc2GvGp2Hm2+Gc1Gc2GvGp2Gp1Hm1
(1)
然后得到Fsp到Tsp的传递函数关系(G(s)的逆),即:
Tsp(s)=G-1(s)Fsp(s)
(2)
根据式(2)就可以把优化得到的副回路流量设定值Fsp转换为主回路的温度设定值Tsp,即通过转换函数G-1(s)来实现优化器得到的流量值,G-1(s)的值要根据串级控制中PID参数的变化进行更新。这种副回路控制器到主回路控制器转换的方法能够应用的前提是Tsp到Fsp的传递函数G-1(s)已知并且是可以实现的,该方法不仅需要准确获得G(s),对模型精度和控制参数要求较为苛刻,而且由于G-1(s)通常不是真分式,导致在工程实际中无法实现。
针对副回路控制器到主回路控制器的变换得到的G-1(s)不可实现的问题,考虑用Tsp到Fsp的传递函数增益的倒数来简化代替G-1(s),即假设G(s)中增益为Kg,其值可通过闭环辨识获得。同时,考虑优化结果的一次下载给对象带了较大的阶跃响应,可能造成系统不稳定及产品质量指标超限等情况[12~14],因而通过滤波器下载,使优化结果的实现更加平稳,滤波器为增益为1/Kg的一阶惯性环节,则:
系统控制结构如图2所示。这种方法可以有效地克服G-1(s)不可实现的问题,在不改变现场控制结构的基础上进行改进从而实现优化,具有结构简单、实现容易及普遍适用性强等优点。
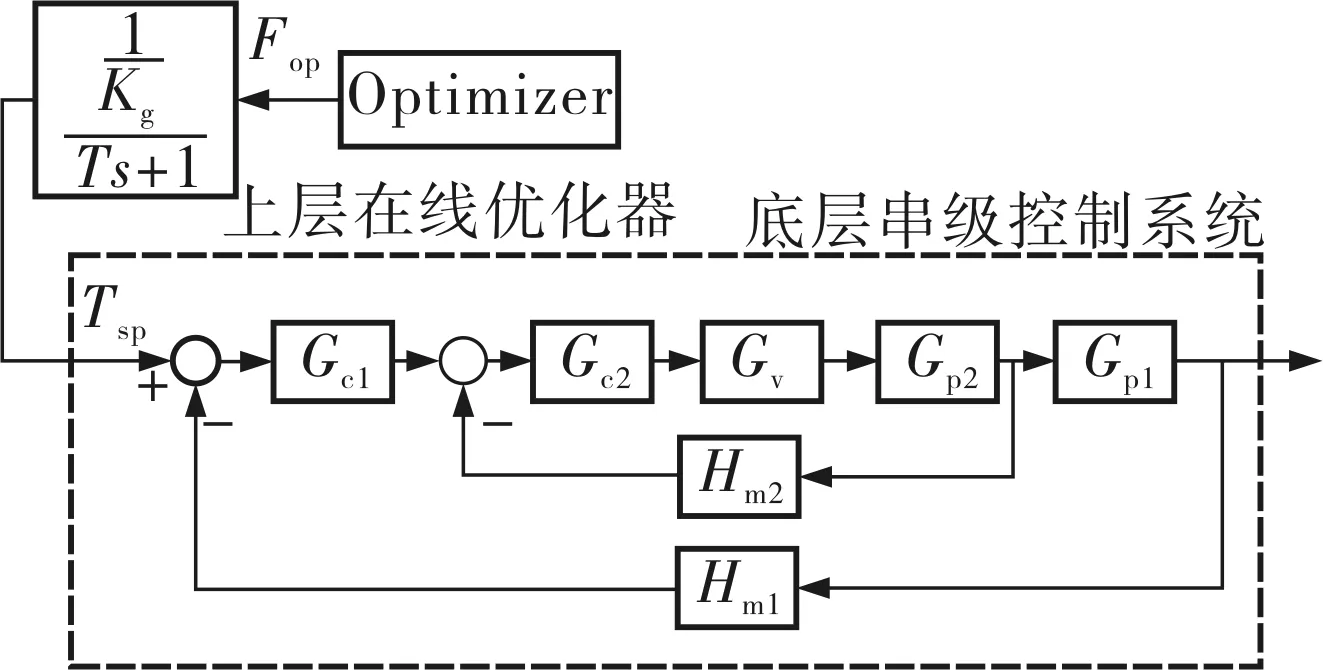
图2 串级控制的在线优化实现结构
3 案例分析
以Henson M A和Seborg D E的串级连续搅拌反应器(Continuous Stirred Tank Reactor,CSTR)[15]为例进行仿真。如图3所示,该反应器由两个连续全混流CSTR反应器串联组成,在两个反应器中发生一阶不可逆放热反应A→B,该过程有一个混合了反应物和溶剂的进料流、一个输出流和一个冷却水流。其中,qc为冷却水流量,q为进料流量,C1、C2为出口浓度,T1、T2为出口温度。

图3 串级CSTR系统
为简化计算,建模时假设系统完全混合并且物理参数是常数,流量在整个过程中维持恒定。系统模型如下:
CSTR中的物料平衡方程
CSTR中的能量平衡方程


其中,反应器体积V1=V2=100L,进料浓度Cf=1mol/L,进料流量q=100L/mol,进料温度Tf=350K,冷却水温度Tcf=350K,反应速率常数k0=7.2×1010min-1,R为理想气体常数,E/R=10000,E为活化能,密度ρ=ρc=1kg/L,U、A分别为热交换系数和面积,UA1=UA2=1670kJ/min,反应热ΔH=-47.8kJ/mol,比热cp=cpc=239J/(kg·K)。
状态变量x、系统输出y和操作变量u定义为:x=[C1,T1,C2,T2]T,y=T2,u=qc。串联CSTR反应器的温度流量串级控制结构如图4所示。设定实际过程的初始状态为x=[0.085,442,0.005,450]T,实施优化前,系统在u=90的条件下达到稳态平衡点,其稳态输出y=455K。对闭环系统辨识,获得流量与温度间传递函数的增益Kg=-2,同时获得系统动态响应的调节时间ts=9s。
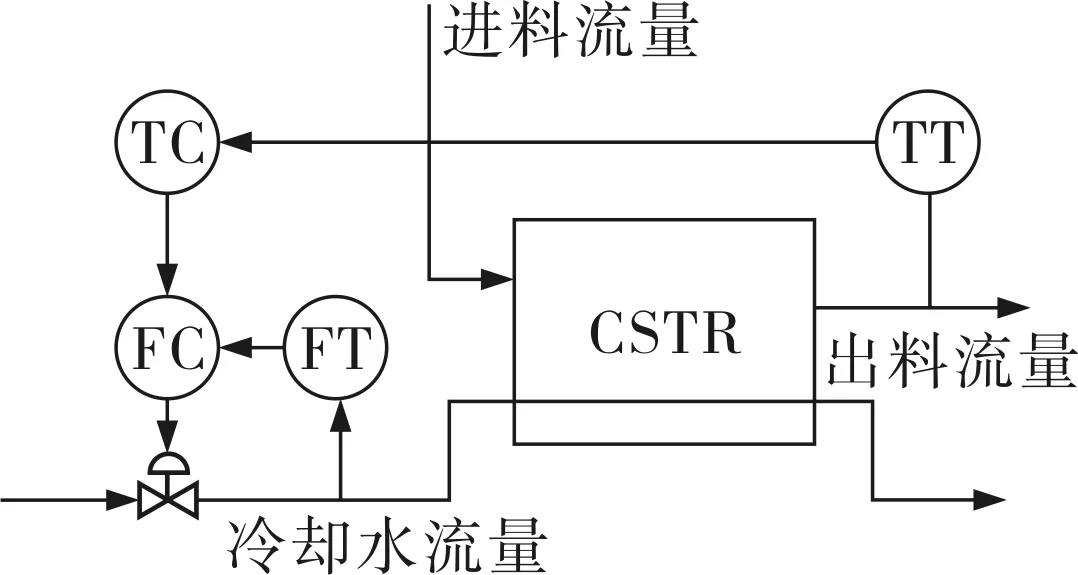
图4 串联CSTR反应器的温度流量串级控制结构
利用ITAE性能指标[16]确定T的最优值。改变3T与ts的比值,即改变优化下载与系统实现的动态响应过程调节时间的比值,得到性能指标值的变化曲线如图5所示。图中虚线为T=0时的ITAE性能指标,以此作为基准,虚线以下的部分为较优值。由图可知,当3T=ts/3时性能指标达到最小,系统性能最优,即T最优值取1s。优化后,性能指标ITAE的具体值由10.5减少到8.7,减少了17%。

图5 ITAE性能指标变化曲线
实施优化前,系统达到稳态,但并非处于过程的最优操作点。假设根据文献[8]中的优化目标函数求得流量设定值需要减少10L/min(设定值由90L/min下降至80L/min)才能达到最优操作点。在仿真时间20s处对串联CSTR反应器实施在线优化,其优化结果如图6所示。图中曲线1为优化结果一次性下载时过程中变量的响应曲线,曲线2为T最优时优化结果下载时过程中变量的响应曲线,曲线3为3T=ts时优化结果下载时过程中变量的响应曲线。由图6可知,不采用滤波器的优化结果一次性下载会产生较大超调,可能引起产品质量指标的超限,不利于生产的平稳进行。T值设置过大虽然保证设定值的平稳加载,但会增加调节时间,延缓了优化目标的实现,影响经济效益。通过优选时间常数T,能够在保证理想调节时间的条件下大大减少超调,快速、平稳地实现在线优化过程。

图6 在线优化过程中变量的响应曲线
4 结束语
针对流量优化变量如何通过现存的“主控制变量-流量”这种典型的化工过程串级控制实现优化目标的问题,分析了几种在线优化实现结构,得出流量优化变量通过一阶惯性环节在主回路上通过主控制变量设定值实现的方案。该方法理论上构思简单,实际中易于实现,具有普遍适用性。一阶惯性优化环节中增益可以通过闭环辨识得到,重点分析了优化环节中时间常数对超调量与动态响应时间的矛盾,实现过快则存在较大超调,甚至可能出现不稳定现象;实现过慢则延缓了优化目标的实现。通过优选时间常数,能够快速、平稳地实现流量优化变量在串级结构中的在线实现,并且不改变现有串级控制结构。
[1] Darby M L,Nikolaou M,Jones J,et al. RTO: An Overview and Assessment of Current Practice[J].Journal of Process Control,2011,21(6):874~884.
[2] Visser E, Srinivasan B,Palanki S.A Feedback-based Implementation Scheme for Batch Process Optimization[J]. Journal of Process Control,2000,10(5):99~10.
[3] 邵之江.连续工业过程的在线优化[D].杭州:浙江大学,1997.
[4] 蒋慰孙,俞金寿.过程控制工程[M].北京:中国石化出版社,2004:240~242.
[5] Zhong Y C, Luo Y.Comparative Study of Single-loop Control and Cascade Control of Third-order Object[J].Procedia Engineering,2011,15:783~787.
[6] 刘涛,张卫东,顾诞英.一类开环不稳定串级控制系统的解析设计[J].控制与决策,2004,19(8):872~876,884.
[7] Abe N,Nakamura A.Learning to Optimally Schedule Internet Banner Advertisements[C].Proceedings of the 16th International Conference on Machine Learning.Slovenia:ICML,1999:12~21.
[8] 杨斌,许锋,罗雄麟.基于动态模型的在线反馈优化[J].化工学报,2012,63(7):2149~2155.
[9] Engell S.Feedback Control for Optimal Process Operation[J].Journal of Process Control,2007,17(3):203~219.
[10] Figueroa J L.Economic Performance of Variable Structure Control: a Case Study[J].Computers & Chemical Engineering,2000,24(8):1821~1827.
[11] 许锋,翟炳鑫,罗雄麟.催化裂化装置分离系统稳态优化及其动态实现[J].计算机与应用化学,2011,28(11):1397~1403.
[12] 翟炳鑫,许锋,罗雄麟.催化裂化装置补充吸收剂流量操作优化及其控制实现[J].化工自动化及仪表,2010, 37(5):72~77.
[13] Finkler T F,Kawohl M,Piechottka U,et al.Realization of Online Optimizing Control in an Industrial Polymerization Reactor[C].Proceedings of the International Symposium on Advanced Control of Chemical Processes.Singapore:IFAC,2012:11~18.
[14] Steinboeck A,Graichen K,Kugi A.Dynamic Optimization of a Slab Reheating Furnace with Consistent Approximation of Control Variables[J].IEEE Transactions on Control Systems Technology,2011,19(6): 1444~1456.
[15] Henson M A,Seborg D E.Input Output Linearization of General Nonlinear Processes[J].AIChE J,1990,36(11):1753~1758.
[16] 徐峰,李东海,薛亚丽.基于ITAE指标的PID参数整定方法比较研究[J].中国电机工程学报,2003,23(8): 207~211.

