变极法设计无刷双馈电机绕线转子的研究
周 韬,陈益广
(天津大学,天津300072)
0 引 言
无刷双馈电机(以下简称BDFM)是一种特种电机。BDFM 的定子上有独立的两套绕组,分别是极对数为p 的功率绕组和极对数为q 的控制绕组;转子绕组能同时产生极对数分别为p 和q、且转向不同的磁动势[1-5]。稳定运行时,两套绕组产生不同速度的旋转磁场不直接耦合,而是通过转子间接耦合,使两套绕组之间产生能量交换。控制绕组接容量较小的双向变频器实现能量的双向流动,因省掉了电刷和滑环,电机可靠性高。
近年来对BDFM 的研究越来越多。文献[6]对级联式双馈电机建立了数学模型,计算绕组电感,并通过建模仿真验证了模型的正确性。文献[7]对级联式无刷双馈电机的动态特性进行了深入研究。文献[8]在深入分析交流电机理论的基础上提出了采用变极法设计绕线转子,此方法可以有效提高槽内导体的利用率,缺点是接线比较复杂。文献[9]对BDFM 不同数学模型进行了梳理与总结分析。文献[10]和[11]分别对等距笼型转子和深槽笼型转子进行了分析研究,都提出了新型的笼型结构,改善了电机性能。但是,围绕改变转子绕组结构来提高p和q 对极下的基波含量、改善电机性能等方面还需要进行深入的分析研究。
本文通过对双速感应电机的分析入手,运用交流电机绕组理论,分析了采用变极法设计3Y / 3 Y型无刷双馈电机绕线转子的原则和步骤,给出了一种5/2 对极的绕线转子设计方案。运用有限元仿真软件对电机进行了仿真,给出了电机的不同工况下绕组感应电动势波形。仿真结果表明,采用变极法设计的绕线转子能够较好地耦合两种极对数的磁场,转子磁动势高次谐波含量较低。定子绕组的感应电动势谐波含量小,波形较好。
1 变极法原理
利用“反向法”[12]实现单绕组双速感应电机变极调速时定子绕组接线图如图1 中3 根虚线不连接时所示。此时,支路b1,b4和b7属于Arp相的三条并联支路,支路b2,b5和b8属于Brp相的三条并联支路,支路b3,b6和b9属于Crp相的三条并联支路,9条支路形成3Y 接三相对称绕组;支路b1,b2和b3属于相的三条并联支路,支路b4,b5和b6属于相的三条并联支路,支路b7,b8和b9属于相的三条并联支路,9 条支路形成新的3Y 接三相对称绕组。当,和三端接入三相对称交流电时,气隙处形成幅值最强的p 对极圆形旋转磁动势;当,和三端接入三相对称交流电时,气隙处形成幅值最强的q 对极圆形旋转磁动势。
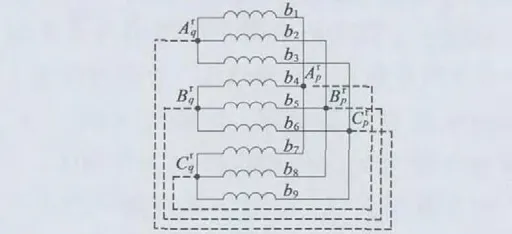
图1 3Y/3Y 换相变极反相序串联转子绕组
电机稳定运行时,定子功率绕组和控制绕组均通入三相对称电流,转子在某一特定转速,即转子同步转速nr下旋转,定子两套绕组形成的旋转磁场能在图1 的转子绕组中同时感应出电动势。
p 对极磁场在转子绕组中感应的电动势频率:
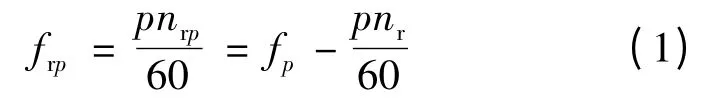
式中:nrp为p 对极磁场相对于转子的转速;fp表示p对极绕组通入电流的频率。
q 对极磁场在转子绕组中感应的电动势频率:
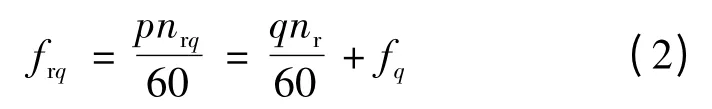
式中:nrq为q 对极磁场相对于转子的转速;fq表示q对极绕组通入电流的频率。
电机实际运行中,双向变频器要时刻调节控制绕组通入电流的频率fq,以满足:

此时,控制绕组中的电流频率与功率绕组中电流频率的关系:
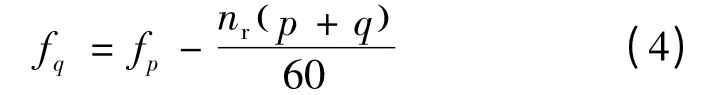
根据式(4)对控制绕组端的电流频率进行控制,保证输出的功率绕组电压频率恒定。这样,在转子同步转速nr下,转子绕组中就能够感应出同一特定频率、幅值较强的感应电动势,并在转子中产生该频率的感应电流。
对于这种连接方式的转子,当三相对称的各并联支路有电流流过时,将同时产生p 对极和q 对极的磁动势。这样定子p 对极功率绕组通入对称电流形成的磁场经过转子的作用会在气隙中同时产生p和q 两种极对数的旋转磁动势。同理,定子q 对极控制绕组中通入的电流通过转子的作用也会在气隙中产生p 和q 这两种极对数的磁动势,而且这两种特定极对数的磁动势幅值较强,其它极对数的谐波磁动势分量较小。
2 设计转子绕组
2.1 设计步骤
采用变极法设计BDFM 转子绕组时,应根据电机的功率和定转子尺寸等选择连接方式。设定、转子的槽数分别为Zs和Zr,功率绕组和控制绕组极对数比为p/q。
现以图1 的3Y/3Y 连接方式为例,给出利用变极法设计转子绕组的基本步骤。
(1)转子槽数Zr的选择。尽量使每极每相的平均槽数是整数,或者是分母为2 的分数。即:
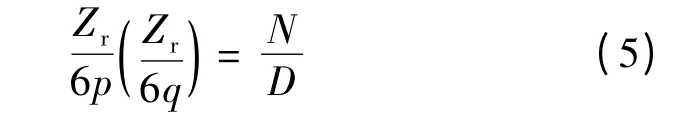
式中:D=1 或2,N 为整数。
(2)确定转子槽数Zr后,分别画出p 对极和q对极下对应的槽号相位图。槽号相位图是由2Zr个数组成的数组,包括1 ~Zr的Zr个正数和-Zr~-1 的Zr个负数。数组顺序排列,排列成为2Zr/p(或2Zr/q)行,这样每行空间占据360°电角度。负数和其对应的正数相差180°电角度。
(3)在q(或p)对极槽号相位图下划分成A、B和C 三个对称相带,每个相带再分成相位基本相同的3 个支路槽号组,并确保这3 个支路槽号组对应到另一极对数下槽号相位图的位置互差120°。为了实现两种连接的绕组在转子槽中都能产生三相对称的磁动势,分相时要兼顾两种极对数,在保证对称前提下尽量分成正规相带,这样才能保证在两种极对数下的绕组分布系数较高。
(4)将q(或p)对极槽号相位图下分成的9 个支路槽号组按图1 接法相连接。
2.2 算例
下面以一个具体例子来说明转子绕组的设计。
转子槽数Zr=60,功率绕组极数2p =10,控制绕组极数2q=4。功率绕组正规120°相带分相,功率绕组分相槽号相位图如图2 所示。控制绕组也按120°相带分相,但是为了提高q 对极绕组分布系数,实际只选取了72°相带下的绝大部分槽号。控制绕组分相槽号相位图如图3 所示。图2 和图3 中带阴影的槽号未被选取。将图3 中选中的槽号分到如图4 所示的b1~b9这9 条支路中,这9 条支路在图2 中也是三相对称的。
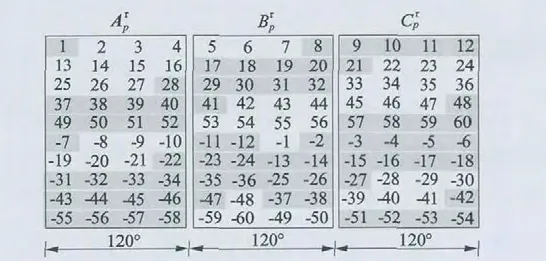
图2 2p=10 极下转子槽号位分相图

图3 2q=4 极下转子槽号位分相图

图4 q 对极下分组支路槽号相位图

图5 5/2 对极60 槽3Y/3Y 换相变极反相序串联转子槽号图
设计每个线圈的匝数时,要综合考虑,以满足槽满率以及形成磁动势对称等要求。图5 为该转子换相变极反相序串联的槽号绕组图。槽号的上标表示对应槽号上的线圈的匝数比,当如图中所示的匝数比绕制时,无论在p 或q 对极下,属于同相的3 个线圈感应电动势相同,属于不同相的线圈产生的感应电动势幅值相同、相位互差120°。转子绕组选择节距时要兼顾两种不同的极对数。这里p/q =5/2,相差较大,当选取线圈上下元件边跨节距y1=17 时,两种极对数下的短距系数分别为kyp=0.965 9 和kyq=0.978 1。虽然线圈端部长一些,但是保证了两种极对数下的短距系数都较高。此种连接转子绕组p,q 两种极对数下的绕组分布系数分别为kdp=0.879 6 和kdq=0.963 9。考虑到每相3 条支路电流的幅值和相位关系,电流利用率[13]为3/4,绕组系数分别为kWp=0.637 和kWq=0.707。
从图5 看出b3,b4,b8这三条支路中含有双倍匝数的槽号,当第一节距y1=17 时,这三条支路中双倍匝数的槽中下元件边位置没有导体,所以双倍匝数的线圈恰好可以占满整个槽。这样基本保证了转子槽满率都比较高。
表1 给出了用上述方法所绕制的转子谐波含量。由表1 可以看出,采用这种变极法设计的转子2 对极和5 对极下的绕组系数较大,转子绕组产生的两种磁动势也较大,而高次谐波含量相对较低,有利于转子绕组与定子两种极对数绕组的耦合。

表1 5/2 对极60 槽3Y/3Y 接法转子绕组谐波分析
3 有限元仿真
3.1 BDFM 模型
定子Zs=54 槽,转子Zr=60 槽,p/q =5/2。定子控制绕组和功率绕组是每极每相下槽数分别为9/2 和9/5,跨距分别为11 和5 的短距分布双层分数槽绕组,转子绕组采用图5 的绕组结构绕制。利用仿真软件建立二维有限元仿真模型。
电机模型具体参数如表2 所示。
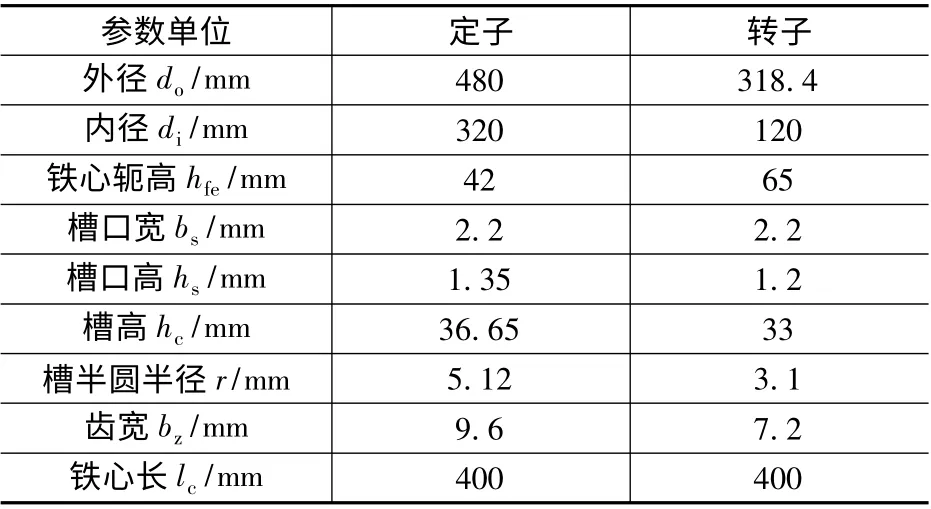
表2 无刷双馈电机的结构参数
3.2 仿真
电机的定转子绕组都为5 匝绕制。电机转子静止,定子其中一套绕组通入工频电流,仿真得到另一套绕组的开路感应电动势。功率绕组通28 A 有效值的工频交流电流,控制绕组感应电动势如图6(a)所示。控制绕组通4 A 有效值、与功率绕组反相序的工频交流电流,功率绕组感应电动势如图6(b)所示。由图6 可见,转子静止时,当定子中的某一套绕组通入对称交流电时,通过转子的耦合可以在另一套绕组感应出同频率的三相对称正弦感应电动势。

图6 转子静止时感应电动势
电机以亚同步转速nr=300 r/min 旋转,根据式(4)得出控制绕组电流频率fq=15 Hz。定子功率绕组通入有效值28 A、频率50 Hz 的交流电流,同时控制绕组通有效值4 A、频率15 Hz 的反相序交流电流。功率绕组感应电动势波形如图7(a)所示;功率绕组感应电动势傅里叶分解如图7(b)所示;电机内部磁力线分布如图8 所示,气隙磁密波形如图9 所示;气隙磁密的傅里叶分解如图10 所示。
气隙磁密大小受定子两套绕组通入电流的影响,当作发电机,转速或转矩改变时,可以通过调节控制绕组输入的电流频率、大小和相位保持功率绕组端电压的稳定。
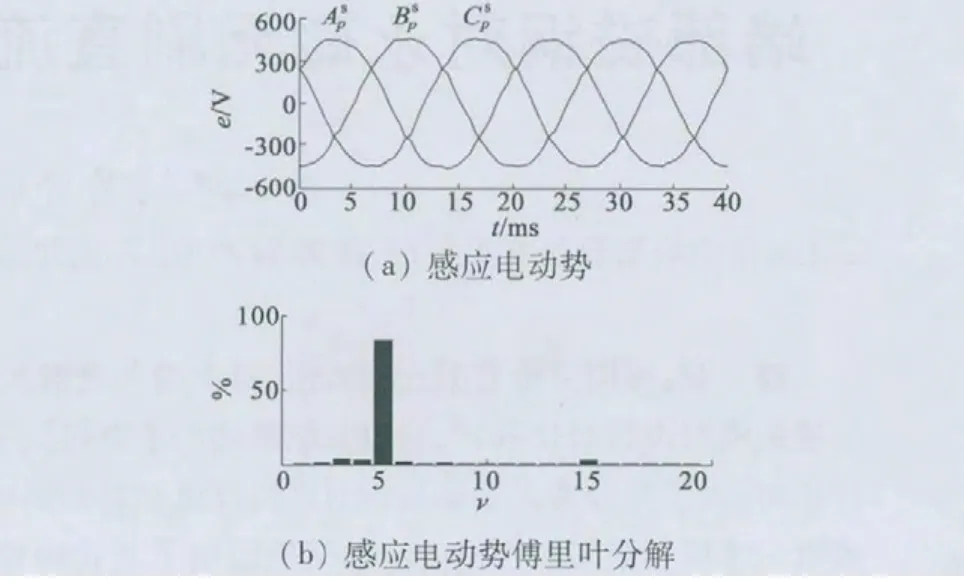
图7 nr =300 r/min 时功率绕组感应电动势及其傅里叶分解

图8 电机内磁力线分布图
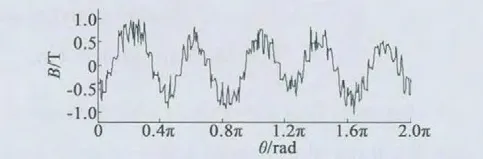
图9 气隙的磁密波形

图10 气隙磁密傅里叶分解
4 结 语
根据变极理论,分析了无刷双馈电机3Y/3Y 型绕线转子的工作原理,介绍了该转子结构的设计原则。电机转子9 条支路组成的两个3Y 接法反相序连接绕组,使不同极对数所对应的3Y 结构支路对称,再通过匝数的选择保证各个支路绕组感应电动势幅值相同。设计了极对数p/q=5/2 的绕线转子,建立了二维有限元模型并进行了仿真。仿真结果表明,利用变极法设计的绕线转子,定子两套绕组感应电动势谐波含量小,为无刷双馈电机绕线转子设计提供了一种可行方案。
[1] RBOERTS P C,MCMAHON R A,TAVNER P J.Equivalent circuit for the brushless doubly fed machine(BDFM)including parameter estimation and experimental verification[J]. IEEE Proceedings on Electric Power Applications,2005,152(4):933-924.
[2] WANG X,MCMAHON R A,TAVNER P J. Design of the brushless doubly- fed (induction)machine[C]//IEEE International Electric Machines and Drive Conference,Antalya,Turkey,2007:1508-1513.
[3] WILLAMSON S,FERRERIA A C,WALLACE A K.Generalized theory of the brushless doubly-fed machine(Part1)[J]. IEE Proceedings on Electric Power Applications,1997,144(2):111-122.
[4] WALLACE A K,SPEE R,LAUW H K. Dynamic modeling of brushless doubly-fed machines[C]//Industry Applications Society Annual Meeting,San Diego,USA,1989:329-334.
[5] RBOERTS P C,MCMAHON R A.Performance of BDFM as generator and motor[J]. IEEE Proceedings on Electric Power Applications,2006,153(2):289-299.
[6] 卞松江,贺益康,潘再平.级联式无刷双馈电机的建模与仿真[J].中国电机工程学报,2001,21(12):33-37.
[7] 高强,韩力,李辉,等.级联式无刷双馈电机的四种动态数学模型[J].微特电机,2010,38(3):18-23.
[8] 王雪帆.一种转子绕组采用变极法设计的新型无刷双馈电机[J].中国电机工程学报,2003,23(6):108-111,127.
[9] 赵荣理,王昕,张爱玲.无刷双馈电机数学模型的研究和分析[J].微特电机,2013,41(7):18-23.
[10] 胡堃,何凤有,薛冰.深槽式笼型转子无刷双馈电机的仿真分析[J].微特电机,2011,39(11):34-36,43.
[11] 邓先明,方荣惠,王抗,等. 等距笼型转子无刷双馈电机的有限元分析[J].电机与控制学报,2009,13(4):507-510,522.
[12] 许实章.交流电机的绕组理论[M]. 北京:机械工业出版社,1985.
[13] 熊飞. 绕线转子无刷双馈电机建模分析和电磁设计研究[D]. 武汉:华中科技大学,2010.

