集成永磁伺服电动机电磁热耦合模型设计与分析
吴轶群
(江苏信息职业技术学院,无锡214153)
0 引 言
随着电力电子技术和微电子技术的发展,可以将永磁伺服电动机、控制器、驱动器和位置编码器组合起来,即集成永磁伺服电动机[1]。与传统伺服电动机相比,集成永磁伺服电动机具有以下优点:体积、质量小;功率密度高;抗干扰能力强;布线简单;维护方便等[2]。但是功率密度的提高,给电机散热带来了许多问题,因此对集成永磁伺服电动机的热分析研究具有理论和实际意义。有限元法作为一种经常使用的数值计算方法,可用于集成永磁伺服电动机的热分析。文献[3-6]对电机进行了三维有限元热分析,在建立热耦合模型时,考虑了电磁损耗;文献[7-9]对电机功率模块和驱动器进行了三维有限元热分析,阐述了电机功率器件的损耗主要来自电机平稳运行时的平均损耗;文献[10]着重分析了高温下永磁材料的不可逆退磁性;文献[11]分析了温度和永磁材料对永磁同步电机的影响。
1 集成永磁伺服电动机简介
集成永磁伺服电动机是电机本体、控制器、逆变器、编码器的集合体,其结构如图1 所示。图1(a)为集成永磁伺服电动机剖视图,位置编码器可将位置信号传输至伺服运动控制器,运动控制器根据位置信号对电机进行控制,将控制信号传输至功率驱动器,功率驱动器主要由前置放大电路、功率MOSFET 和保护电路组成。图1(b)为集成永磁伺服电动机外形示意图。
由图1 可知,集成永磁伺服电动机的结构比较紧凑,缩短了编码器与控制器、逆变器与电机本体之间的连接长度,可以减小外界对位置信号的干扰,有利于提高驱动能力,非常适合模块化设计。与相互分离、相对独立的伺服电动机与伺服控制驱动器相比,集成永磁伺服电动机在一定程度上解决了工业现场走线复杂、维护困难、驱动能力下降等难题,增强了系统的可靠性,降低了系统的故障率。但是作为一个高度耦合的复杂系统,集成永磁伺服电动机在运转过程中,往往存在高频电磁场、多变温度场等问题[12]。

图1 集成永磁伺服电动机结构示意图
2 电磁热耦合模型建立
对于集成永磁伺服电动机来说,为简化其模型,便于计算,可做如下假设:电机材料各向同性,不考虑铁心饱和、集肤效应等问题;电机的电导率、磁导率保持不变,温度影响忽略不计[13]。那么基于有限元的电磁仿真模型可以表示:

式中:Ω 为求解域;u 为磁导率;σ 为电导率,A =[AxAyAz]T为磁位移矢量;J = [JxJyJz]T为源电流密度;S 为边界条件。
集成永磁伺服电动机三维热分析模型如图2 所示,电机各组件材料属性如表1 所示。那么电机的暂态三维热传导模型可以表示:

式中:T 为电机温度;λ 为电机热导率;Q 为电机内部热生成;ρ 为电机平均密度;c 为电机平均比热。

图2 集成永磁伺服电动机三维热仿真模型

表1 集成永磁伺服电动机各组件材料属性
考虑到电机边界条件,其热传导方程可表示:

式中:q 为电机表面热流量;n 为电机表面边界向量。根据伽辽金方程基本原理,将热传导方程离散化可得:
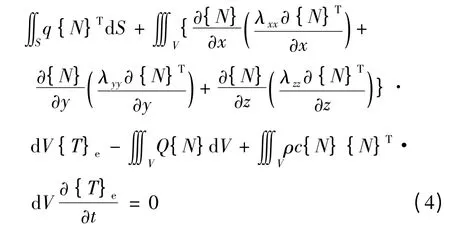
式中:{N}为插值函数。
若将对流和辐射作为边界条件,则存在如下等式:

式中:hc为对流系数;he为辐射系数;ε 为电机表面热发射率;σc为斯蒂芬-玻尔兹曼常数;F*为辐射面形状系数;Tout为外部环境温度。
综上所述,同时包含热传导、对流和辐射的有限元热平衡方程可以表示:

式中:K 为热传导矩阵;{ }T 为节点温度向量;C 为热容矩阵;{ }F 为节点热通量。而且:
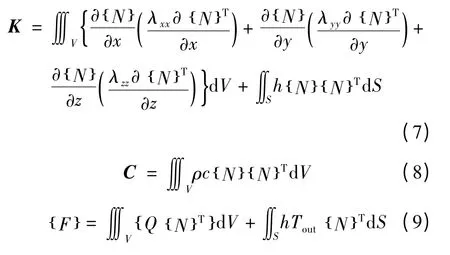
3 热载荷及热边界条件确定
3.1 热载荷确定
一般情况下,热载荷主要指热流量、热流率和内部热生成。集成永磁伺服电动机的热载荷只有内部热生成,而且热生成主要来自系统各部分的损耗[14]。
(1)电机铁损
电机铁损主要由电机定子与转子铁心产生,而且其分布比较复杂。通过精确的建模和剖分,利用有限元法计算模型中每个时刻、每个网格的磁通密度来获取电机的铁损分布。电机铁损由磁滞损耗physt、涡流损耗peddy和附加损耗pex组成,即:

但是通过有限元法计算得到铁损会比实际值小,可根据电机铁损的实测值对仿真数值进行修正,以确保热载荷的准确性。
(2)绕组铜损
电机绕组铜损包括I2R 损耗和导线涡流损耗,其中绕组I2R 损耗可以表示:

式中:Te1为电机运行周期;iu,iv和iw分别为电机三相电流;Ru,Rv和Rw分别为三相电阻。
(3)驱动电路损耗
驱动电路的损耗主要由开关管及续流二极管的导通损耗和开关损耗组成:
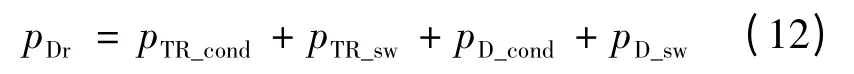
式(12)中pTR_cond,pTR_sw分别为开关管的导通及开关损耗;pD_cond,pD_sw分别为续流二极管的导通及开关损耗。
3.2 热边界条件确定
一般情况下,热边界条件主要包括给定温度、对流和辐射[15]。对于集成永磁伺服电动机,其内部的对流情况十分复杂,故本文重点讨论对流热边界条件。考虑到所有的对流均满足牛顿冷却公式,那么式(5)可简化:

在实际的传热过程中,对流换热系数不仅取决于电机各组件材料属性、热交换表面形状等,而且与流体的流速有关。
对于自然对流,不论是层流状态还是湍流状态,电机表面的等效对流换热系数均可由下式计算得到:


式中:g 为重力加速度;β 为热膨胀系数;Ts为表面温度;T∞为外界流体温度;v 为粘滞系数;α 为热扩散系数。
对于气隙对流,层流和湍流可能同时存在,往往以气隙中的雷诺数Reag和气隙临界雷诺数Reacr进行区分[16]。当Reag<Reacr时,气隙中的空气流动为层流,有效导热系数近似为空气的导热系数;当Reag>Reacr时,气隙中的空气流动为湍流,有效导热系数:


式中:ω 为转子旋转角速度;δ 为电机气隙长度。电机气隙中的临界雷诺数Reacr可以表示:

4 仿真与实验分析
4.1 电磁损耗仿真与实验分析
为确定集成永磁伺服电动机的电磁损耗,本文分别进行仿真和实验。仿真用电机的参数:额定功率400 W,额定转速3 000 r/min,额定电压60 V,电机铁损计算基于硅钢片35ww400 损耗-频率曲线。
实验测试条件:采用速度闭环控制,电机转速为3 000 r/min,脉宽调制频率15 kHz,额定电压60 V,额定输出功率400 W。经仿真和实验,电机各部分具体损耗值如表2 所示。

表2 电机各部件仿真和实测损耗
通过对比表2 中的仿真损耗和实际损耗可知:由于网格细分不够、涡流损耗系数、迟滞损耗系数和杂散损耗系数不够精确,导致定子铁损、转子损耗比实测损耗小;同样,功率模块的仿真损耗也比实测损小,主要原因在于实测损耗包含了控制电路损耗、编码器电路损耗和采样功率电阻损耗等。由上述分析可得,为保证集成永磁伺服电动机热分析的准确性,需将仿真得到的损耗结果乘以一个修正系数,并以修正结果作为基准进行热仿真分析。
4.2 热仿真与实验分析
通过对集成永磁伺服电动机的电磁损耗分析,可以得到其修正后的电磁损耗密度分布。针对集成永磁伺服电动机的热仿真,首先,将电机的电磁损耗密度直接导入其ANSYS 热模型中;然后,将对流、辐射等边界条件施加到电机各表面;最后,对集成永磁伺服电动机进行热仿真分析,持续时间为30 min,仿真结果如图3 所示。

图3 集成永磁伺服电动机温度分布
另外,本文对集成永磁伺服电动机进行了温升实验。实验条件如下:室温27℃、自然冷却;负载1.27 N·m;转速3000 r/min;持续时间为30 min。实验过程中,由温度成像仪对不同时刻的电机表面温度进行测量并与仿真结果比较,结果如图4 所示。

图4 电机表面实测与仿真温度曲线
通过对比相同时刻的电机表面温度可知,对于最低温度,仿真与实测结果基本一致;而对于最高温度,虽然实测结果略低于仿真结果,但最大温差并没有超过4℃,导致此温度差的主要原因在于:(1)为计算方便,仿真模型忽略了若干散热结构,导致集成永磁伺服电动机表面仿真温度高于实测温度;(2)在建立电机热仿真模型时,很难准确定义材料属性和各部分之间的热阻,同样会导致仿真结果与实测结果的不同。
通过上述分析可知,仿真温度与实测温度的误差在允许范围内,说明本文建立的电磁热耦合模型和热传导分析方法是可行的、有效的,能够较好地预测电机的温升。
5 结 语
由于体积较小、集成度较高,所以集成永磁伺服电动机存在较高的功率密度,在一定程度上会给电机带来较高的温升。本文重点研究了集成永磁伺服电动机系统的温度场分布,在简要介绍集成永磁伺服电动机结构的基础上,基于有限元法建立了电机的电磁热耦合仿真模型;根据系统的温度变化,建立了非线性的热边界条件。通过仿真、实验以及数据对比验证,结果表明所建模型较为准确、有效。
[1] LEE B H,KIM K S,JUNG J W,et al. Temperature estimation of IPMSM using thermal equivalent circuit[J].IEEE Transactions on Magnetics,2012,48(11):2949-2952.
[2] ZHAO N,ZHU Z Q,LIU W. Rotor eddy current loss calculation and thermal analysis of permanent magnet motor and generator[J]. IEEE Transactions on Magnetics,2011,47(10):4199-4202.
[3] HUANG Y,ZHU J,GUO Y.Thermal analysis of high-speed SMC motor based on thermal network and 3-D FEA with rotational core loss included[J]. IEEE Transactions on Magnetics,2009,45(10):4680-4683.
[4] 邰永,刘赵淼. 感应电机全域三维瞬态温度场分析[J]. 中国电机工程学报,2010,30(30):114-120.
[5] LI Weili,QIU Hongbo,YI Ran,et al.Three-dimensional electromagnetic field calculation and analysis of axial-Radial flux-type high-temperature superconducting synchronous motor[J]. IEEE Transactions on Applied Superconductivity,2013,23(1):520-527.
[6] CHEN H,XU Y,LU H H. Analysis of temperature distribution in power converter for switched reluctance motor drive[J]. IEEE Transactions on Magnetics,2012,48(2):991-994.
[7] 陈明,胡安.IGBT 结温模拟和探测方法比对研究[J]. 电机与控制学报,2011,15(12):44-49.
[8] ZHOU P,LIN D,XIAO Y,et al.Temperature-dependent demagnetization model of permanent magnets for finite element analysis[J]. IEEE Transactions on Magnetics,2012,48(2):1031-1034.
[9] WANG J,WANG W,ATALLAH K,et al.Demagnetization assessment for three-phase tubular brushless permanent-magnet machines[J].IEEE Transactions on Magnetics,2008,44(9):2195-2203.
[10] LI Weili,QIU Hongbo,ZHANG Xiaochen,et al.Influence of copper plating on electromagnetic and temperature fields in a high-speed permanent-magnet generator[J].IEEE Transactions on Magnetics,2012,48(8):2247-2253.
[11] KULKARNI D P,RUPERTUS G,CHEN E.Experimental investigation of contact resistance for water cooled jacket for electric motors and generators[J]. IEEE Transactions on Energy Conversion,2012,27(1):204-210.
[12] TENCONI A,PROFUMO F,BAUER S E,et al.Temperatures evaluation in an integrated motor drive for traction applications[J].IEEE Transactions on Industrial Electronics,2008,55(10):3619-3626.
[13] PETERS T B,McCARTHY M,ALLISON J,et al.Design of an integrated loop heat pipe air-cooled heat exchanger for high performance electronics[J]. IEEE Transactions on Components,Packaging and Manufacturing Technology,2012,2(10):1637-1648.
[14] 李伟力,宋成宇,李立毅,等. 轴-径向磁通全超导同步电动机的磁场分析[J]. 中国电机工程学报,2011,31(12):96-101.
[15] JUNGREUTHMAYER C,BAUML T,WINTER O,et al. A detailed heat and fluid flow analysis of an internal permanent magnet synchronous machine by means of computational fluid dynamics[J].IEEE Transactions on Industrial Electronics,2012,59(12):4568-4578.
[16] ZHANG Y,RUAN J,HUANG T,et al. Calculation of temperature rise in air-cooled induction motors through 3-D coupled electromagnetic fluid-dynamical and thermal finite-element analysis[J]. IEEE Transactions on Magnetics,2012,48(2):1047-1050.

