基于Maxwell 压铸机用永磁同步电动机优化分析

杨国龙，黄开胜，陈文敏，郑景东

(1.广东工业大学，广州510006;2.东莞电机有限公司，东莞523000;3.广东电网有限责任公司湛江供电局，湛江524000)

0 引 言

近年来，随着铸造行业的迅速发展，压铸机是现代压力铸造生产中不可缺少的基础技术设备。通常以压铸件的要求作为压铸机发展方向，对于压铸件的应用范围很广，在汽车等交通工具、机械、电子、电气、通讯设备、精密仪表仪器、建筑构件、高档家电、体育用品和日用品等诸多行业中，都大量采用了压铸件，其中用量最多的是汽车工业［1］。同时人们对压铸机的要求越来越高，要求压铸机节能、环保、结构紧密，而永磁同步电动机是一种新型的高效特种电机，具有结构简单、体积小、重量轻、高效节能、功率密度高等特点，能够广泛应用于压铸机行业中［2］。

永磁同步电动机一直存在齿槽转矩的问题，过大的齿槽转矩会导致电动机的输出转矩波动较大，引起其振动和噪声，更为严重的是影响电动机的性能，因此，削弱永磁同步电动机的齿槽转矩是高性能永磁同步电动机在设计和制造过程中必须考虑和解决的关键问题［3］。

本文针对一款压铸机用永磁同步电动机存在较大的转矩波动，首先分析永磁同步电动机齿槽转矩产生原理，导出齿槽转矩解析表达式。根据该款电动机的尺寸参数，利用Maxwell 2D 有限元软件建立电动机有限元模型，通过对磁极的偏移角度进行扫描分析得出，对磁极偏移恰当的角度能明显削弱电动机的齿槽转矩［4］。根据优化后电动机尺寸参数试制样机，利用电机测试平台，测得样机的性能得到明显改善，同时验证Maxwell 2D 有限元仿真软件正确性。

1 永磁同步电动机齿槽转矩的分析

1.1 齿槽转矩产生原理

当永磁同步电动机绕组不通电时，永磁体与铁心之间相互作用而产生的转矩称为齿槽转矩。它由永磁体和电枢齿相互作用力的切向分量引起的，若永磁同步电动机的定、转子之间有相对运动，基本能够保持永磁体和永磁体极弧部分的电枢齿之间的磁导恒定，因此，该永磁体极弧部分对应的电枢齿周围的磁场也几乎保持不变，但是在一段由永磁体两侧面对应一个或两个电枢齿组成的区域中，磁场储能的变化是由于该区域磁导变化较大引起的，进而产生齿槽转矩。在永磁电机绕组不通电时，其磁场能量W 对于定、转子位置角α 的负导数被定义为齿槽转矩，即:

1.2 齿槽转矩的解析分析

为便于分析，假设永磁材料的磁导率与空气相同，永磁电机的电枢铁心磁导率为无穷大，因此电动机内存储的能量可近似为永磁体中储存的磁场能量和电动机气隙的磁场能量叠加，可表示:

永磁同步电动机的永磁体性能、结构尺寸以及定、转子之间的相对位置决定其磁场能量，气隙磁密沿电枢表面分布可近似表示:

把式(3)代入式(2)进行整理，又可以表示:

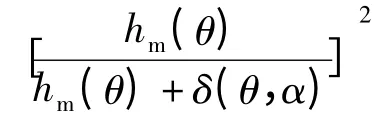
1.3 磁极偏移与齿槽转矩的关系分析

当永磁同步电动机的磁极进行磁极偏移后，在[－π，π ]上分别对(θ)和进行傅里叶分解，(θ)的分布情况如图1 所示，其中p 为电机的极对数，θ1～θ2p分别为各个磁极所偏移的角度。

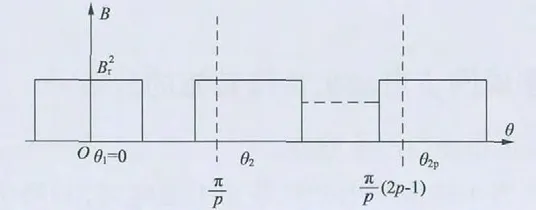
图1 永磁体偏移时(θ)示意图

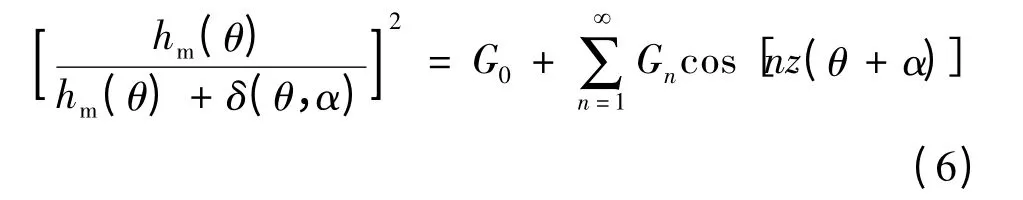
将式(4)～式(6)代入式(1)，得到磁极偏移后齿槽转矩的表达式:

式中:LFe为电枢铁心的长度;R1为电枢外径;R2为电枢内径;n 为使为整数的整数。Branz和Brbnz分别表示:

式中:dp为永磁体的极弧系数。当永磁体不偏移时(即θk=0)，此时Branz的值恒为零，此时Branz可表示:

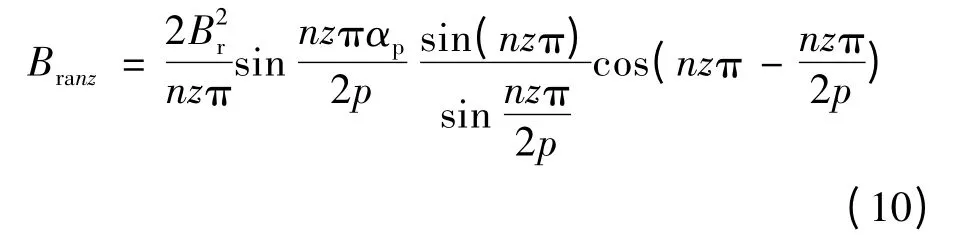
只有当n 为Np的倍数时，Branz才不为零，Np满足:

式中:2p 为电机极数;z 为槽数;GCD(z，2p)为2p 和z 的最大公约数。

由式(8)～式(10)分析可知，当永磁体对称分布时，n 只有取值为Np的倍数时，该次齿槽转矩的谐波才不为零。由此可得，磁极偏移对槽极配合为整数的永磁电动机的齿槽转矩削弱效果明显［6］。

2 永磁同步电动机主要参数及有限元模型建立

根据公司给定一款压铸机用永磁同步电动机的尺寸参数，基于Maxwell 2D 建立该款电机有限元模型。

永磁同步电动机主要技术指标如表1 所示。

表1 主要尺寸参数和指标

利用ANSYS/Maxwell 分析永磁同步电动机瞬态的电磁过程。首先建立永磁同步电动机的有限元模型，如图1 所示。建模步骤如下:

(1)根据给定的电动机尺寸参数和主要技术指标，首先利用ANSYS/RMxprt 模块对电动机进行设计，再将电动机从RMxprt 模块导入Maxwell 2D 模块生成二维有限元模型。

(2)在Maxwell 2D 有限元模型中对定子、转子铁心材料及磁钢属性分别进行重新设置。

(3)通过对电动机各自动生成的剖分尺寸分别进行细剖分，细分尺寸为自动生成剖分尺寸的1/3 ～1/4，使之达到合理的剖分效果，从而使得仿真结果更为精确。

(4)确定电动机在求解过程中的激励源、运动部分及边界条件。

(5)确定电动机的额定负载、求解时间和步长。

利用Maxwell 获得空载和负载情况下电动机的各种性能数据，为了使电动机更加符合实际工况下的空载运行条件，若要对电动机的瞬态磁场进行空载仿真时，可设置电枢绕组的激励为零。负载仿真时，电枢绕组的激励设置为电流源，运动部分重新设置［7］。

图2 永磁同步电动机有限元模型

3 分析磁极偏移对永磁同步电动机齿槽转矩影响

由于该款电动机磁极对称分布，利用Maxwell有限元分析软件，生成电动机1/2 模型。通过分析电动机磁极偏移不同角度时电动机齿槽转矩变化的情况，从中找出最佳的磁极偏移角度使得齿槽转矩最小。磁极偏移情况如下:磁极1、2 逆时针偏移，磁极3、4 顺时针偏移，其中磁极2、3 偏移角度为θ1，磁极1、4 偏移角度为θ2，磁极位置及偏移方向如图3所示。

图3 磁钢位置和偏移方向

根据实际工况确定偏移角度θ1，θ2的关系，取θ2=3θ1，在Maxwell 中将磁极偏移角度设为变量，并对偏移角度进行扫描，得到齿槽转矩最小的偏移角度，齿槽转矩优化曲线如图4 所示。

图4 齿槽转矩优化曲线

根据齿槽转矩优化曲线图，记录每一组［θ1，θ2］齿槽转矩峰值的大小，选择齿槽转矩峰值最小的一组［θ1，θ2］作为磁极偏移的最佳角度，如表2 所示。

表2 磁极偏移的齿槽转矩峰值表

由表2 可以看出，电动机齿槽转矩峰值并不是随着磁极偏移的角度增大而单调递减。而是随着偏移的角度不断增加而齿槽转矩峰值逐渐变小，从而达到最佳的偏移角度，当偏移角度大于最佳偏移角度时，偏移的角度增加会使齿槽转矩的峰值也逐渐增大。因此，存在一个最佳的偏移角度，使得齿槽转矩峰值最小，此时当磁极θ1偏移角度为0.5°，磁极θ2偏移角度为1.5°时，齿槽转矩峰值仅为0.104 N·m［8］。

4 永磁同步电动机有限元仿真结果分析

通过有限元分析软件扫描及分析磁极偏移的角度，选取一组最佳偏移角度使得齿槽转矩达到最小作为磁极偏移的角度，将永磁同步电动机磁极未偏移和偏移合适角度的齿槽转矩进行对比，如图5 所示。

图5 磁极偏移前后齿槽转矩曲线

由图5 可得，电机磁极未偏移时齿槽转矩峰值为1. 209 N·m，磁极偏移后齿槽转矩峰值仅为0.095 4 N·m，齿槽转矩峰值降低了1.11 N·m，磁极偏移后齿槽转矩峰值仅占额定输出转矩0.023%。对磁极偏移后的电动机进行仿真分析，得到该电动机的输出转矩，如图6 所示。

图6 电动机输出转矩曲线

由图6 得知，通过对该款电动机的磁极偏移合适角度后，使该电动机平均输出转矩为410.03 N·m，转矩波动仅0.920 4 N·m，占额定转矩0.22%，结果表明，该电机输出转矩平稳。

5 试制样机并进行验证

利用有限元分析软件得到磁极偏移的最佳角度，根据公司给定该款永磁同步电动机的尺寸参数，采用磁极最佳的偏移角度对磁极进行偏移，制作样机，如图7 所示。

图7 样机定、转子结构图

给该电动机施加340 V 相电压，利用电动机的实验平台对样机的性能进行测试，得出实验数据，将样机测试数据与Maxwell 2D 仿真结果进行对比，如表3 所示。

表3 Maxwell 仿真值与样机测试值

由表3 对比分析可得，Maxwell 软件的仿真值与样机测试值比较接近，误差均在5%以内，电动机的性能满足给定要求。

6 结 语

本文针对一款压铸机用永磁同步电动机存在较大的齿槽转矩，从而引起电机输出转矩波动较大，采用磁极偏移方法降低电机齿槽转矩，利用Maxwell软件分析获得该款电机磁极偏移的角度，通过对磁极偏移合适角度使齿槽转矩降低1.11 N·m。根据电机尺寸，制作样机并进行试验验证，样机测试值与Maxwell 仿真值的误差在5%以内，在工程允许范围内，因此，对永磁同步电动机的磁极偏移合适角度后，电机运行平稳，各项性能良好。目前，该款电机已小批量生产，电机实际使用效果良好，得到用户的认可及好评。

［1］ 孟岳.基于有限元与人工神经网络方法的压铸机结构优化的研究［D］.合肥:合肥工业大学，2011.

［2］ 暨绵浩.永磁同步电动机及其调速系统综述和展望［J］. 微特电机，2007，35(3):49－52.

［3］ 谭建成.永磁无刷直流电机技术［M］.北京:机械工业出版社，2011.

［4］ 杨玉波，王秀和，张 鑫，贺广富.磁极偏移削弱永磁电机齿槽转矩方法［J］.电工技术学报，2006，21(10):22－25.

［5］ 王秀和.永磁电机［M］.北京:中国电力出版社，2010.

［6］ 刘婷. 表贴式永磁同步电机齿槽转矩削弱方法研究［D］. 长沙:湖南大学，2012.

［7］ 赵博，张洪亮.Ansoft12 在工程电磁场中的应用［M］. 北京:中国水利水电出版社，2010.

［8］ 郭仁，黄守道，高剑，等.一种基于磁极偏移的永磁电机齿槽转矩最优削弱方法［J］.微特电机，2010，38(10):31－33.