Halbach 永磁伺服电动机气隙磁场优化研究
吉 智,包西平
(徐州工业职业技术学院,徐州221140)
0 引 言
所谓电机优化是指在必要的约束条件下优化电机参数,使电机某些性能指标水平得到提高[1]。当需优化的变量和约束条件较多,同时变量间又存在交叉影响时,电机性能优化问题就变复杂了,需选取合适的优化方法才能达到性能最优。
随着电机优化研究的不断发展,最近几年以来,优化方法有以下一些新的突破和发展[2-6]:
(1)优化算法的新突破[7-9]。如模式搜索法、遗传算法等在优化效果、优化速率与可靠性等方面得出了许多改进的方法。
(2)提出混合优化算法[10]。根据实际需要,发挥各种优化方法各自优势,将其进行有效组合,可得到效果更优的混合优化算法。
(3)完善和建立电机优化的专家系统。在电机优化中,专家系统对不能用精确模型描述或本身规律尚不明确的对象,可能有意想不到的良好效果。
电机优化的首要问题是构造能反映优化指标的目标函数。由于气隙磁场的性能和分布质量能够从多方面反映和影响电机性能,是电机优化参数中具有代表性一个,而一般用气隙磁场的基波幅值和畸变率来反映磁场性能和分布质量,因此本文构造了一个能够反映磁场畸变率的目标函数,而将基波幅值作为磁场优化的约束条件。
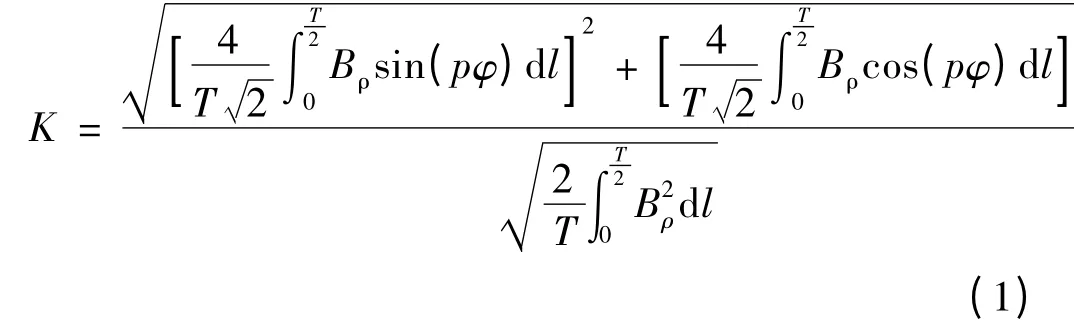
定义:

经验可知,气隙磁场为正弦时k =1,而气隙磁场为非正弦时k <1,磁场越接近正弦,k 越逼近1。所以目标函数Cost的值,气隙磁场对正弦的畸变率越小,k 值越趋近0;反之,则越趋近1。本文在下面讨论的优化方法中将Cost优化期望确定为“望小”。
本文以图1 所示的110st-m02020 型永磁电机为优化对象,选取五个对Halbach 永磁伺服电动机气隙磁场影响较大的参数:磁极厚度thk、气隙长度t、充磁角a、主辅磁极弧长比k、极弧系数emb。测量原型电机上述参数,得出其五个参数初值,如表1 所示。

图1 原型电机

表1 原型电机参数
1 Halbach 永磁伺服电动机气隙磁场的优化
1.1 模式搜索(PS)法优化
对气隙磁场的参数进行PS 算法优化,PS 优化五个参数初始值、单位及取值范围如表2 所示。
启动PS 算法,经过112 次迭代,其中图2 为迭代过程;在迭代中磁场正弦畸变率与磁密基波幅值如图3 所示;迭代后最优点如表3 所示。最后最优点的选择应综合考虑磁场正弦畸变率和磁场磁密基波幅值。原则是在气隙磁场磁密基波幅值≥0.75 T的情况下,气隙磁场正弦畸变率望小。

表2 需优化的变量及其取值范围
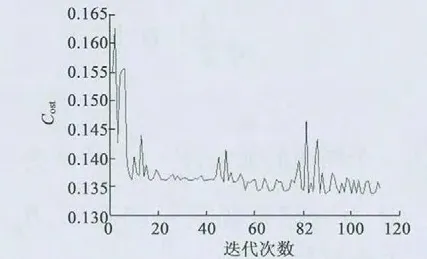
图2 PS 算法迭代过程
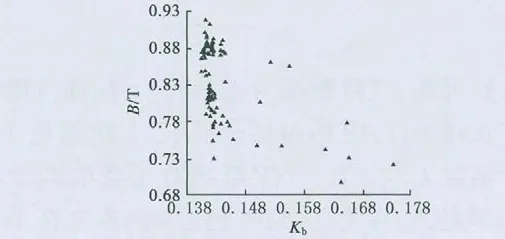
图3 PS 算法迭代点对应的基波幅值与畸变率
PS 优化的初始点取表1 中的参数,该参数记作“初始点1”,经PS 优化获得最优点记作“初始点1”;对比分析的需要,同时选取“初始点2”,优化后最优点记作“优化点2”。将两次优化结果列于表3中。从表3 中可知,PS 优化后从Cost、Kb、B 值可知,初始点1“较优”,而初始点2“较差”。另外选择不同的初始点会造成PS 优化效果的差异,PS 算法优化时初始点的选择不同会收敛于不同的局部最优点。这表明PS 算法在局部初始点附近的区域内具有很强的搜索能力。因此,我们可以先采用全局搜索能力强的算法进行初步优化,搜索到全局最优点附近区域内的某一点,然后将其作为PS 算法的初始点进行二次优化,利用PS 优化算法较强的局部搜索能力,将大大提高搜索到全局最优点的概率。

表3 PS 优化的最优点
1.2 遗传算法(GA)优化
以原型电机气隙磁场的五个参数值为初始值进行GA 优化,如下表4 和图4 所示,优化的迭代过程如图5 所示,采用经典的GA 遗传算法。GA 优化开始后,经过315 次迭代,迭代点对应的基波幅值与畸变率如图6 所示,GA 优化后参数值及Cost,Kb,B 值如表5 所示。
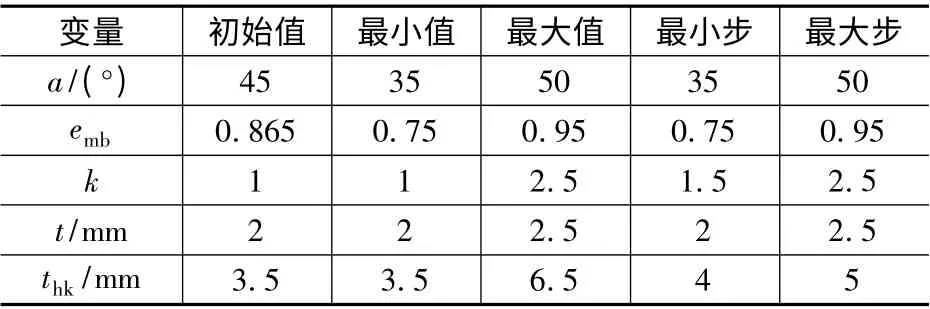
表4 GA 优化的变量及变量取值范围

图4 GA 仿真参数

图5 GA 优化迭代过程

图6 GA 优化迭代点对应的基波幅值与畸变率

表5 GA 优化后参数值及Cost,Kb,B 值
GA 优化具有较强的全局搜索能力,能够在优化的迭代过程中跳出局部区域,在全局区域内更广泛的搜索全局最优点。但也有明显的缺点:在迭代过程中易发生搜索点的大幅度跳变,特别是在搜索后期接近全局最优点时,迭代点仍会发生剧烈跳变,迭代点可能会远离全局最优点,使其效率下降。因此,为提高整体优化效率,需在GA 优化后期引入局部搜索能力较强的算法。
1.3 田口(Taguchi)法优化
在田口法优化中,为了尽快找出最优点可能存在的区间,第一轮试验中对各参数尽可能采取较多的水平进行试验,因此采用5 因素5 水平试验表,即L25(55),具体如表6 所示。

表6 第一轮实验点及目标函数值
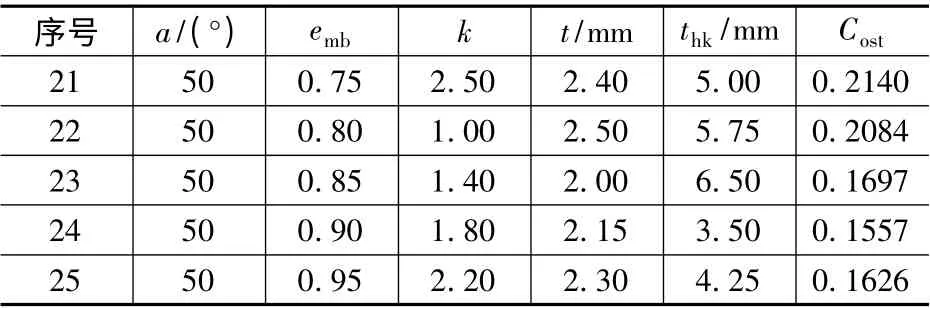
续 表
从表7、表8 均值方差分析和响应表可知,五个参数影响Cost值的程度有较大差别。表7 的P 值(检验水平)是变量,不会明显影响试验结果的概率,P≤0.01 说明参数会特别明显地影响试验结果,0.01 <P≤0.05 说明参数会明显影响试验结果,P >0.05 说明参数对试验结果没有多大的影响。因此从表中数据知,emb参数会特别明显地影响试验结果,而其它参数对试验结果影响不明显,各参数影响的显著性相差很大。这些和表8 中Δ 值的结果一致。某参数对结果影响不明显,并非在后面试验时可以忽略,而仅仅将其当作次要因素考虑。

表7 均值的方差分析
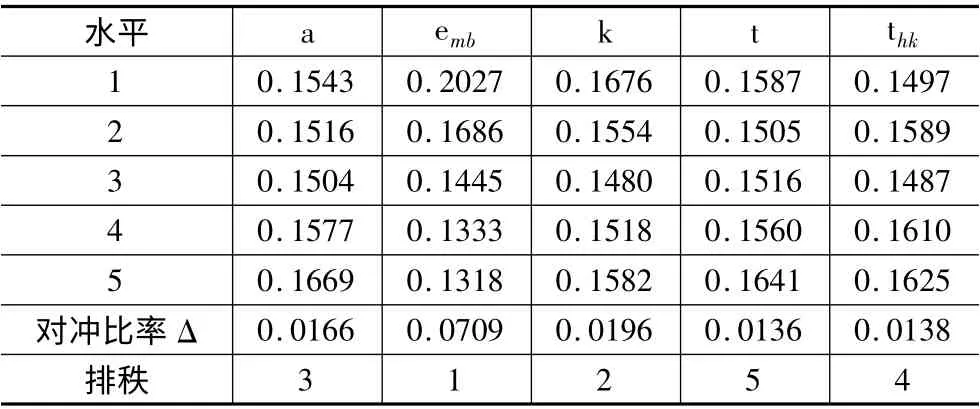
表8 均值响应表
经过5 批共89 次迭代,各轮试验后Cost值的分布如图7 所示,迭代点对应的磁密基波幅值与分布如图8 所示,各批次试验点及推算点如表9 所示。5个批次中第5 批试验点为最优点,即表9 中的第九个点。由图7 知,第一轮试验Cost值波动最大,数值很大、很小的点都存在。第2、3、4、5 轮实验Cost值波动越来越小,各轮之间还存在交叉,这表明目标函数值已收缩到非常小的区域了。
由以上可知,田口法主要在第1、2 轮对气隙磁场的优化效果较好,优化后期的3 轮试验效果较差。因此,田口法也具有较强全局搜索能力,在优化初期能够高效率地搜索到全局最优点的大致范围,但在逼近最优点的优化后期,其效率却明显降低。
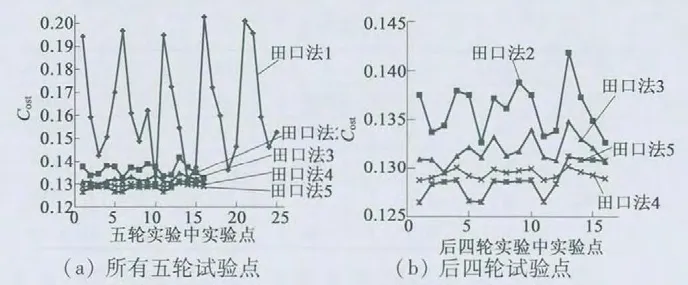
图7 目标函数值在每轮实验中的分布
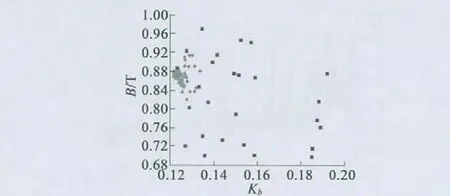
图8 迭代点对应的磁密基波幅值与畸变率分布

表9 每轮的试验最优点和推算最优点
2 Halbach 永磁伺服电动机气隙磁场的新型优化方法
根据前面的三个优化试验,可以看出Halbach电机气隙磁场三种优化方法特点:GA 算法和田口法在搜索全局最优点大致范围的迭代初期,效率较高,但从搜索到的某点开始搜索全局最优点的后期过程中,优化效率明显下降。而PS 法却与上述两种方法的特点相反,所以可将GA 算法、田口法分别与模式搜索法组合,参考有关文献[11-20],我们提出了两种新型混合优化方法:田口-PS 混合优化;GA-PS 混合优化。
2.1 田口-PS 混合优化
在前述田口法五轮试验中选取最优点作出发点,优化参数选取与前面相同,然后再用PS 法进行后期的优化,表10 为三种优化结果对比。

表10 GA 优化后参数值及Cost,Kb,B 值
从表10 可看出,先进行田口优化,再进行PS 优化,获得全局的最优点Kb值有一定的降低,但降低幅度不大,但与直接PS 优化相比,Kb值有较大幅度下降。可知:1)田口法可以较好的优化Halbach 电机气隙磁场,经较少轮次便可较好地逼近全局最优点;2)田口-PS 新型混合优化法比田口法优化效果有一定的提高,但由于田口法优化所得最优点已非常逼近全局最优点,因此效果未有明显提升;3)从表10 比较Cost,Kb,B 值可知,田口-PS 算法和田口算法优化效果均明显优于PS 算法。
2.2 GA-PS 混合优化
先进行GA 优化,然后再利用其结果进行PS 优化,表11 为两种优化结果的对比。由数据对比可知,GA-PS 混合优化比GA 优化具有更好的优化效果,Kb值从13.039 5%降低至12.140 2%。
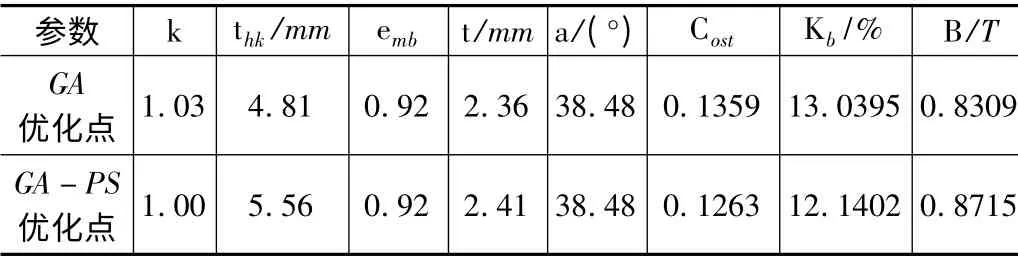
表11 对比两种优化方法的结果
2.3 比较五种优化结果
对气隙磁场的五个参数分别进行田口、GA、PS、田口-PS、GA-PS 优化,图9 为对比五种优化结果各参数值波形图,磁场强度与畸变率比较如图10 所示。
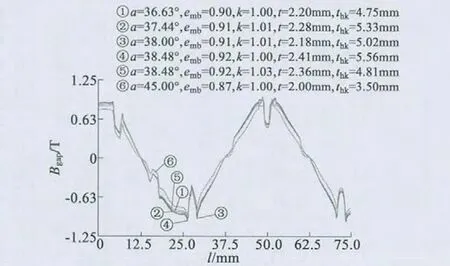
图9 不同优化结果波形对比

图10 五种优化结果对比
从上述原型电机和五种优化结果对比知,PS、GA 优化的结果相似,与原型电机相比气隙磁场的畸变率明显降低;而田口、田口-PS、GA-PS 优化结果也较接近,相对于PS、GA 优化效果有明显提升。
3 结 语
针对Halbach 永磁伺服电动机气隙磁场的优化,本文构造了一个能够较准确的反映气隙磁场正弦性的目标函数Cost。选取一台较合理的Halbach原型电机参数,将PS 法、GA 法和田口法应用于Halbach 永磁同步电机气隙磁场优化,研究得出:GA 法的全局搜索能力很强,但后期局部搜索能力差;田口法全局搜索能力较强,但后期局部搜索能力也较差。而PS 法的局部搜索能力很强,但初始点的选取对搜索效果有较大影响,不同的初始点,相同参数下,优化结果往往差距较大。
根据上述三种算法特点,作者提出了田口-PS和GA-PS 两种新型混合算法。仿真实验表明:两种新型优化算法能够吸取和结合原算法的优势,取长补短,使优化效果和质量有明显提升,而且在一定的优化精度要求下可减少大量迭代计算的过程。将新型混合优化方法用于Halbach 电机气隙磁场的优化,可明显提升优化效果,具有较强的实用性。
[1] 吉智.高性能永磁同步伺服系统关键技术研究[D]. 徐州:中国矿业大学,2013.
[2] 翟旭平. 基于遗传算法的异步电机多目标优化设计的研究[D].南京:东南大学,2000.
[3] 陈世坤.电机设计[M].北京:机械工业出版社,1997.
[4] 唐任远.现代永磁电机理论与设计[M]. 北京:机械工业出版社,1997.
[5] 王充权.电机的计算机辅助设计与优化技术[M]. 上海:上海交通大学出版社,1989.
[6] 卢刚,李声晋,马瑞卿,等.电机CAD 技术[M].北京:国防工业出版社,1997.
[7] MIRZAEIAN B,MOALLEM M,TAHANI V,et al.Multiobjective optimization method based on a genetic algorithm for switched reluctance motor design[J].IEEE Transactions on Magnetics,2002,38(3):1524-1527.
[8] 汪洁,樊叔维.遗传算法的改进及其在电机优化设计中的应用[J].西安交通大学学报,2004,27(2):41-46.
[9] 樊叔维,张兴志.全局优化算法自适应模拟退火-遗传算法的研究[J].光学精密工程,1999,7(4):16-19.
[10] 方瑞明,翟旭平,胡虔生.多轮遗传算法在电机优化设计中的应用[J].微电机,2002,35(3):12-16.
[11] NYANTEH Y,EDRINGTON C,SRIVASTAVA S,et al. Application of artificial intelligence to real-time fault detection in permanent magnet synchronous[J]. IEEE Transactions on Motors Industry Applications,2013,49(3):1205-1214.
[12] 方瑞明,翟旭平,胡虔生.多轮遗传算法在电机优化设计中的应用[J].微电机,2002,35(3):12-16.
[13] MIRZAEIAN B,MOALLEM M,TAHANI V,et al.Multiobjective optimization method based on a genetic algorithm for switched reluctance motor design[J].IEEE Transactions on Magnetics,2002,38(3):1524-1527.
[14] 汪洁,樊叔维.遗传算法的改进及其在电机优化设计中的应用[J].西安交通大学学报,2004,27(2):41-46.
[15] 樊叔维,张兴志.全局优化算法自适应模拟退火-遗传算法的研究[J].光学精密工程,1999,7(4):16-19.
[16] 方瑞明,翟旭平,胡虔生.多轮遗传算法在电机优化设计中的应用[J].微电机,2002,35(3):12-16.
[17] 王凌.智能优化算法及其应用[M]. 北京:清华大学出版社,2001.
[18] 邢文训,谢金星.现代优化计算方法[M].2 版. 北京:清华大学出版社,2005.
[19] HOOKE R,JEEVES T A. Direct search solution of numerical and statistical problems[J]. Association for Computing Machinery,1961,8(2):212-229.

