重载列车动能闯坡计算方法及应用

王开云， 黄 超

(西南交通大学牵引动力国家重点实验室，四川 成都610031)

牵引定数是牵引区段内的牵引质量标准.统一区段内的牵引定数可以减少货物列车在区段站、编组站的作业，从而提高铁路运输能力并加速机车和车辆的周转，具有显著的经济效益［1-2］.随着我国重载铁路运输的发展，各主要货运干线的牵引定数不断增大，由于干线与支线的线路平纵断面存在较大差异，牵引定数增加之后，在干线上可正常运行的货物列车行驶到支线上时可能面临动能闯坡问题.所谓动能闯坡，是指利用机车牵引力和坡前储存的动能，使列车以不低于机车计算速度闯过坡顶.

对于列车的操纵问题，主要研究方向有两个:一是列车的节能操纵研究［3-5］;二是组合列车的制动操纵研究［6-7］.目前，对于列车闯坡操纵的研究较少，仅在坡停事故的分析中有所提及，如文献［8-9］提出在不超速情况下，尽可能提高坡底速度，采用“闯爬结合”的方式通过困难坡道. 由于这些操纵建议并未考虑具体的线路平纵断面条件及列车编组特性，研究结论是定性的，具有一定的局限性.

本文基于列车纵向动力学理论，考虑列车纵向运动的所有因素［10-11］，提出了一种计算列车最低闯坡速度的方法，并结合某重载铁路工程实际，开展了长大重载列车在实际坡道上的操纵分析，研究结果可为司机闯坡前的抢速操纵提供参考.

1 动能闯坡的多质点模型

1.1 列车的多质点模型

在研究列车动能闯坡问题时，忽略机车车辆横向力和垂向力的影响，将每节机车车辆简化为一个只有纵向自由度的质点，整列车(由n 节机车车辆编组而成)抽象为一个多质点的弹簧阻尼系统.每节车辆上的受力情况如图1 所示.

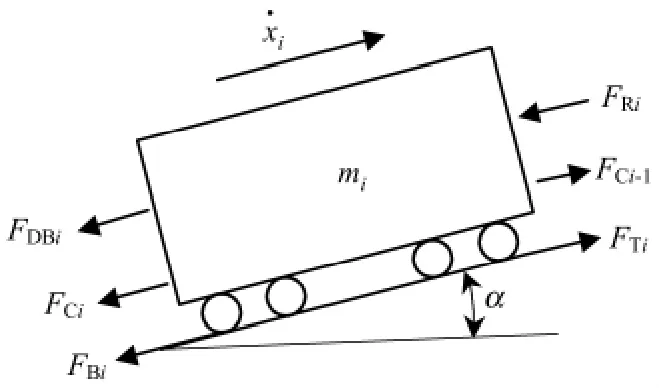
图1 第i 节车的受力示意Fig.1 Schematic force diagram of vehicle i

图1 中，α 为第i 节车所处线路断面的坡度，其纵向动力学微分方程为

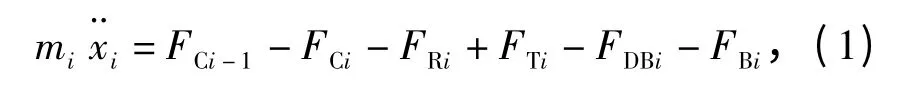
式中:i=1 ～n;

mi为第i 节车的质量;

FCi-1为第i 节车的前车钩力，当i = 0 时，FCi-1=0;

FCi为第i 节车的后车钩力，当i=n 时，FCi=0;

FRi为第i 节车的运行阻力，包括基本运行阻力、坡道阻力、曲线阻力、起动阻力等;

FTi为机车牵引力，仅作用于机车;

FDBi为机车的动力制动力，仅作用于机车;

FBi为第i 车的空气制动力.

对于由n 节机车车辆编组而成的列车，可列出n 个运动微分方程，组成二阶微分方程组. 本文采用新型显式积分方法对此方程组进行数值积分［12］求解.

1.2 坡道简化分类方法

在牵引区段内，使牵引重量受到限制的困难坡道称为限制坡道，其余的坡道则为非限制坡道. 根据限制坡道所处的位置和长度不同，可将其分为计算坡道和动能坡道［13］，如表1 所示.

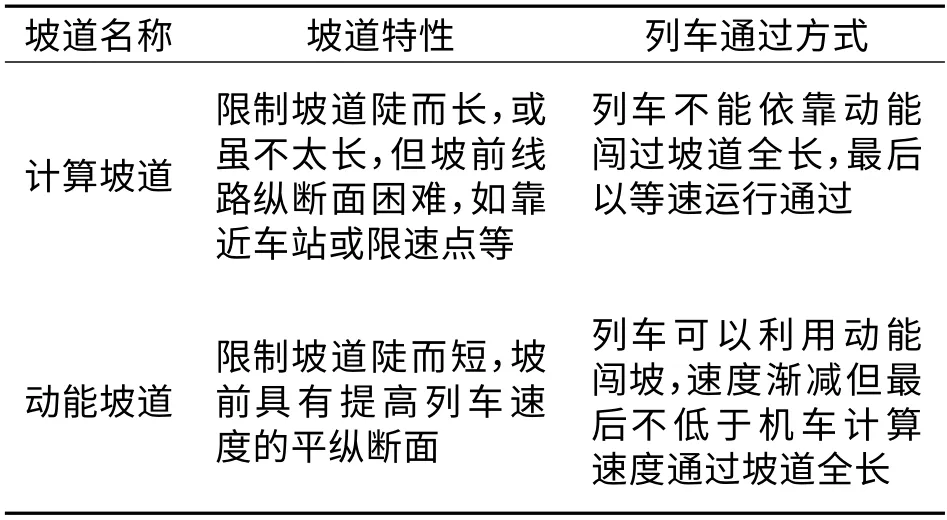
表1 限制坡道的分类Tab.1 Classification of limited slope

由表1 可知，限制坡道的分类需要根据具体线路纵断面的情况，结合理论和实践的经验来判断，需综合考虑的因素比较多，不适合快速化和流程化地分类.

对于已经给定的列车编组，按照列车在计算坡道上以机车计算速度等速运行时，列车受到的总阻力和机车计算牵引力(乘以牵引力使用系数)相等的原则，可得到，即

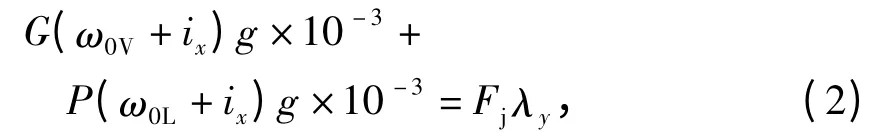
式中:G 为牵引质量，t;

P 为机车质量，t;

Fj为机车计算牵引力，kN;

λy为机车牵引力使用系数，取为0.9［14］;

ω0L、ω0V分别为计算速度下机车、车辆单位基本阻力，N/kN;

ix为计算坡度;

g 为重力加速度.

由式(2)可得到给定编组列车的计算坡度为

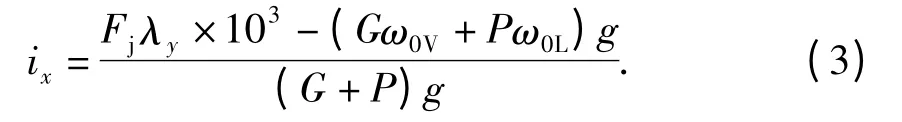
对于已经给定的列车编组及线路平纵断面，首先按式(3)推导出其计算坡度ix，然后将ix与线路中的坡道坡度α 相比较. 简化的坡道分类方法如表2 所示.

表2 简化的坡道分类方法Tab.2 Simplified classification of the slopes

2 最低速度计算法及其计算流程

在整个动能闯坡过程中，机车以最大牵引力运行，按列车所受到的阻力与机车牵引力的大小不同，可将动能闯坡分为3 个工况.

在列车从平道驶入动能坡道的过程中，列车所受到的阻力逐渐增大，当阻力与机车牵引力相等时，列车的速度达到最高，此时列车的位置如图2(a)所示，将此过程称为第1 工况.

在列车驶出动能坡道的过程中，列车所受到的阻力逐渐减小，当阻力与机车牵引力相等时，列车的速度达到最低，此时列车的位置如图2(b)所示，将此过程称为第3 工况.列车从最高速度位置驶向最低速度位置时，其受到的阻力先增大后减小，列车的速度逐渐降低，将此过程称为第2 工况.

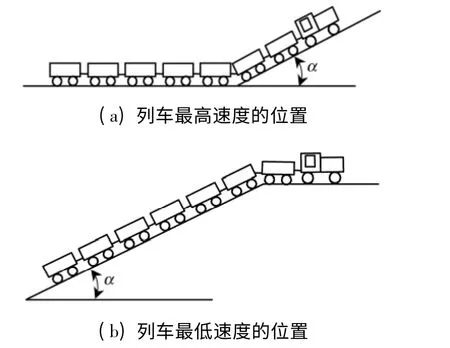
图2 列车闯坡示意Fig.2 Sketch of train rushing through a slope

当采用单质点模型分析动能闯坡问题时，列车最低速度恰好出现在坡顶位置［13］，当采用多质点模型研究动能闯坡问题时，不妨以首位机车速度及其所处位置作为整列车的速度和位置，则列车最低速度出现在坡顶之后. 为便于叙述，仍将其称为坡顶速度，并作为列车闯坡性能的评判指标［10］.

假定计划开行的列车编组分别以初速vb1、vb2、vb3从动能坡道前的指定地点出发，计算得到其对应的坡顶最低速度分别为vt1、vt2、vt3，在坡顶速度-初始速度坐标系中，由A(vb1，vt1)、B(vb2，vt2)、C(vb3，vt3)3 个点拟合出一条样条曲线，如图3 所示.根据机车计算速度vj在拟合的样条曲线上通过插值得到对应的最低速度vbmin，即为列车从指定地点开始动能闯坡的最低速度. 需要说明，由于1.2 节中提出的限制坡道简化分类方法并没有考虑坡道前的纵断面情况，因此在计算出α 各动能坡道闯坡所需的最低速度vbmin后，还需检验相应坡道前的闯坡条件. 若坡前有限速点且限速vx≥vbmin，则列车可以利用动能通过此坡道;若限速vx＜vbmin，则列车不能采用动能闯坡的方式通过此坡道，可以采用增加补机等其他措施后再进行列车动能闯坡校验.具体的计算流程如图4 所示.

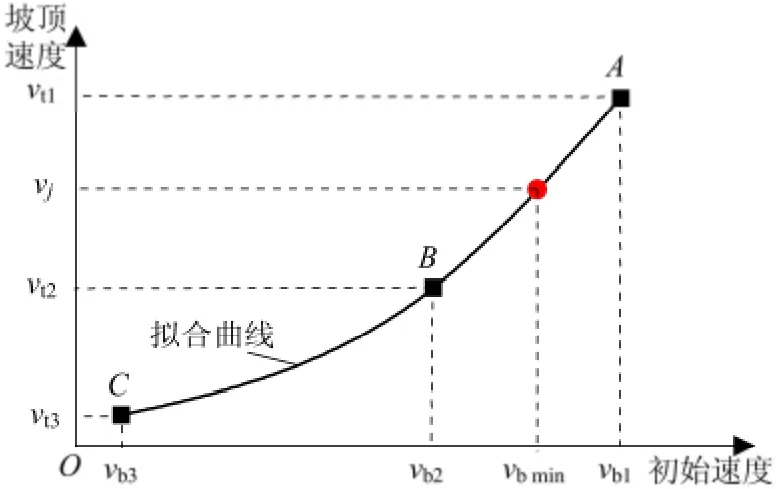
图3 最低速度计算法示意图Fig.3 Schematic calculation ofthe minimum speed

图4 最低速度计算法流程图Fig.4 Flow chart of calculation of the minimum speed

3 工程应用研究

3.1 工程背景简介

为缓解我国能源运输的紧张局面，某运煤专线计划增开万吨重载列车.此货运干线为我国西煤东运的通道之一，重车方向最大上坡道坡度为4.0‰，支线为某火电厂的运煤线路，重车方向的最大上坡道坡度为9.0‰.计划增开的列车编组形式为2 台SS4 机车重联牵引108 辆KM70 货车，列车的主要参数如表3 所示.

表3 列车的主要参数Tab.3 Main parameters of the train

SS4 型电力机车的牵引特性曲线如图5 所示，其中，0 ～50 km/h 速度段受机车粘着力限制，粘着系数按式(4)计算.

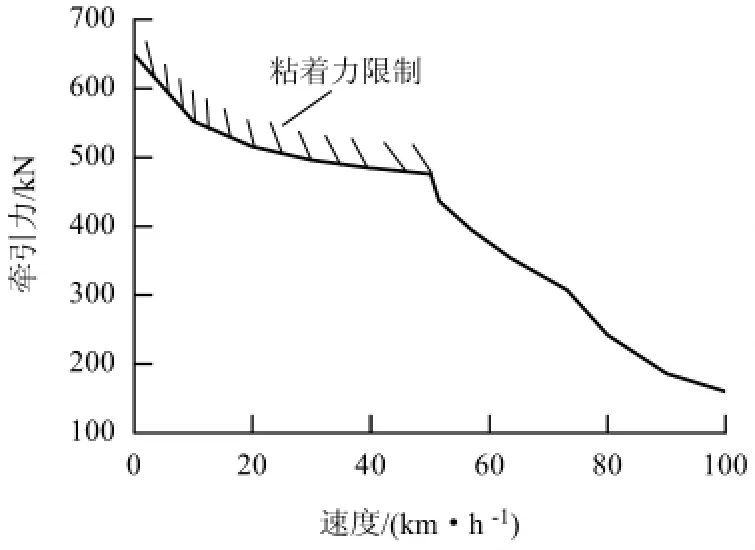
图5 SS4 型电力机车牵引特性曲线Fig.5 Tractive characteristic curve of SS4 locomotive

式中:v 为机车速度.

由式(3)计算可知，给定编组列车的计算坡度为6.1‰，小于货运支线的最大坡道，因此，计划增开的万吨列车在货运支线上运行需进行动能闯坡的计算校验.

3.2 最低速度计算法的计算

图6 给出了此货运支线的路肩高程图.从图6可以看出，在K15 ～K20 范围内存在一个大坡道区段，具体的平纵断面如图7 所示，图7 中:R 为线路平面曲线半径，m;L 为线路曲线长度，m.

从图7 中可以看出，在此区段内存在多个动能坡道，由于它们彼此相邻或相距较近，因此，将此区段视为一个动能坡道，可作为最低速度法计算应用的工况.

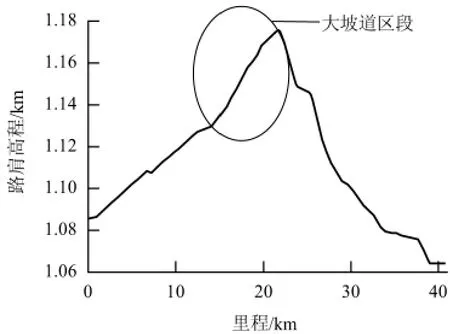
图6 路肩高程图Fig.6 Elevation map of road shoulder

假设列车首位机车位于K14 +100 处时开始动能闯坡，此时列车的初始速度分别为60. 00、70.00、80.00 km/h.两台机车的牵引手柄从零档位提升至最高档位用时32 s，之后一直保持最高牵引档位运行直至通过此区段.

图7 大坡道区段平纵断面示意Fig.7 Schematic of plane and vertical sections of long steep slope

图8 给出了3 种不同初速的列车从K14 +100处运行时，其运行速度随线路里程的变化.从图8 可以看出，3 种列车在通过此区段过程中的最低速度分别为48.14、50.73、53.93 km/h.

如图9 所示，在坡顶速度-初始速度坐标系中，由D(60，48.14)、E(70，50.73)、F(80，53.93)3 点进行样条曲线拟合，并在拟合的曲线上查找SS4 机车的计算速度(vj=51.50 km/h)所对应的初始速度.通过插值可以得到点G(72.8，51.5). 由此可知，给定编组的列车在K14 +100 处利用动能通过大坡道区段的最低闯坡速度为72.80 km/h.

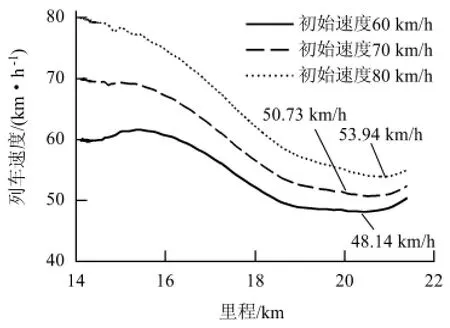
图8 不同初始速度条件下列车速度与里程的关系Fig.8 Train speed versus mileage for different initial speeds

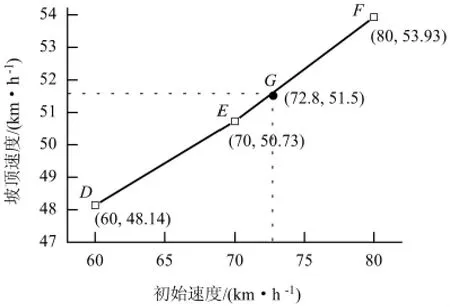
图9 坡顶速度与初始速度的关系Fig.9 Train speed on top of slope versus initial speed

3.3 最低速度法的验证

假定此货运支线在K14 +100 处没有限速点，由3.2 节可知列车的最低闯坡速度为72.80 km/h.为验证动能闯坡最低速度计算法的精确性，对计划开行的万吨编组列车在K14 +100 处以72.80 km/h的初速度实施动能闯坡进行了仿真计算，仿真结果如图10 所示.

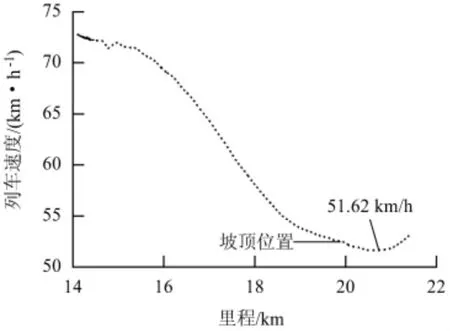
图10 列车速度与里程的关系Fig.10 Train speed versus mileage

从图10 可以看出，列车在通过此区段过程中的最低速度为51.62 km/h，与SS4 机车的计算速度51.50 km/h 相比仅差0.23%，因此，本文提出通过插值计算得到列车最低闯坡速度的方法具有较高的精度.

4 结束语

基于列车纵向动力学理论，考虑线路的平纵断面因素，提出了一种计算列车动能闯坡最低速度的方法.结合工程实际，进行了扩编列车动能闯坡最低速度的计算研究，并对计算结果进行了计算验证，结果表明，该方法具有较高的精度.列车闯坡操纵时，建议在动能坡道前及时提速，以使列车闯坡时的速度不低于计算出的动能闯坡最低速度.

［1］ 夏波，杨浩. 实施长交路、提高牵引定数的经济效益分析［J］. 铁道运输与经济，2004，28(10):9-10，60.XIA Bo，YANG Hao. The economic profit analysis of long locomotives routing and high tonnage rating［J］.Railway Transport and Economy，2004，28(10):9-10，60.

［2］ 袁敏红，张超. 统一牵引定数发展始发直达列车［J］. 中国铁路，2007(7):55-57.YUAN Minhong，ZHANG Chao. Unify tonnage rating and develop nonstop train［J］. Chinese Railways，2007(7):55-57.

［3］ LIU Rongfang，GOLOVITCHER I M. Energy-efficient operation of rail vehicles［J］. Transportation Research Part A:Policy and Practice，2003，37(10):917-932.

［4］ 李波. 基于遗传算法的列车节能操纵曲线寻优［D］.成都:西南交通大学，2007.

［5］ 唐海川，朱金陵，王青元，等. 一种可在线调整的列车正点运行节能操纵控制算法［J］. 中国铁道科学，2013，34(4):89-94.TANG Haichuan，ZHU Jinling，WANG Qingyuan，et al. An on-line adjustable control algorithm for on-time and energy saving operation of trains［J］. China Railway Science，2013，34(4):89-94.

［6］ 李蔚，陈特放，李辉，等. 重载组合列车分布动力机车重联控制系统无线传输同步性研究［J］. 中国铁道科学，2011，32(6):102-106.LI Wei，CHEN Tefang，LI Hui，et al. Research on the wireless transmission synchronization of the coupling control system for heavy haul combined train and distributed power locomotive［J］. China Railway Science，2011，32(6):102-106.

［7］ 赵鑫，王成国，马大炜. 机车无线同步控制技术对2 万t 重载组合列车纵向力的影响［J］. 中国铁道科学，2008，29(3):78-83.ZHAO Xin，WANG Chenguo，MA Dawei. Influence of locomotive wireless sync control technology on the longitudinal force of 20 000 t heavy haul combined train［J］. China Railway Science，2008，29(3):78-83.

［8］ 闫永平，吴宜诚. 重载列车途停原因分析及对策［J］. 铁道机车车辆，2010，30(4):83-86.YAN Yongping，WU Yicheng. Analysis on heavy haul train in-section halt and its countermeasures［J］.Railway Locomotive ＆ Car，2010，30(4):83-86.

［9］ 甘雄华，李彬，邵育华. HXD1C 型机车坡停原因分析及防止措施［J］. 电力机车与城轨车辆，2011，34(1):69-72.GAN Xionghua，LI Bin，SHAO Yuhua. Analysis on HXD1C locomotive in-section halt and its countermeasures［J］. Electric Locomotives ＆ Mass Transit Vehicles，2011，34(1):69-72.

［10］ 铁道部科学研究院机车车辆研究所. TB/T 1407—1998 列车牵引计算规程［S］. 北京:中国铁道出版社，1998.

［11］ 严隽耄，翟婉明，陈青，等. 重载列车系统动力学［M］. 北京:中国铁道出版社，2003:40-125.

［12］ ZHAI Wanming. Two simple fast integration methods for large-scale dynamic problem in engineering［J］.International Journal for Numerical Methods in Engineering，1996，39(24):4199-4214.

［13］ 孙中央. 列车牵引计算实用教程［M］. 北京:中国铁道出版社，2005:178-180.

［14］ 王凤臣，任良抒，丁菊霞. 电力机车牵引计算［M］.成都:西南交通大学出版社，2010:179.