基于DBNs 的车辆悬架减振器异响鉴别方法
黄海波, 李人宪, 杨 琪, 丁渭平, 杨明亮
(1. 西南交通大学机械工程学院,四川 成都610031;2. 西南交通大学信息科学与技术学院,四川 成都610031)
国内外对减振器异常噪声的鉴别方法研究较少,还处于起步阶段.文献[1-2]将台架试验减振器活塞杆顶端相邻加速度峰值衰减量作为减振器异响的鉴别指标,取得了一定的效果,但该方法的鉴别准确率不高.文献[3-4]将台架试验减振器活塞杆顶端加速度信号做了功率谱变换,找到减振器异响的主要频率范围,以此范围内的功率谱均方根值作为异响鉴别指标,提高了辨识的准确度,但异响频段的截取难以准确界定.文献[5-6]根据减振器工作的特点,将活塞杆顶端加速度信号经过小波变换求出换向冲击瞬间的特征能量,聚合了减振器异响的信息,鉴别准确度较高,但该方法前期的数据预处理与计算十分复杂,影响了其广泛应用.
以上减振器异响鉴别方法都是依靠人工经验提取异响的主要特征,要求工程师对减振器的构造及原理要有深层次的认识,往往需要长时间积累和反复摸索,这是一个不可扩展的途径[7]. 基于统计模型的BP(back propagtion)神经网络、逻辑回归与支持向量机等[8-11]可从训练样本中学习获得统计规律,这些模型虽然可以将原始信号数据作为输入,但是模型本质上是属于无隐含层或单隐含层的浅层结构,对数据富含的内在信息提取有限,并且在样本特征维数较高或者含有大量噪声的情况下应用受限,所以在多数情况下仍以人工提取特征作为输入.若能在保证准确率的情况下直接根据传感器收集的信号对减振器异响进行辨识,这将使鉴别工作变得更加容易,深度学习[12-14](deep learning,DL)即为此思想奠定了基础.
深度学习从仿生学的角度模拟人脑进行分析,本质上是含有多层隐含层的神经网络,但有别于传统的浅层模型,其实质是通过“逐层初始化”来克服深度模型在训练上的难度,通过多隐含层来逐级学习数据当中的有用信息,从而提升预测或者分类的正确率.本文开展了减振器整车试验以及减振器台架试验,得出减振器整车与台架试验之间的一致性规律,并基于深度学习提出了减振器异响鉴别的新方法.
1 减振器异响试验分析
1.1 减振器整车试验
减振器是否异响需要经过专业评审团评价将其量化.首先进行减振器整车道路试验. 由于减振器异响具有随机性,常常在车辆低速驶于不平路面时产生,经过大量的整车道路试验,并考虑消除发动机的噪声干扰,最终选择车辆在坡度约为8%的坑洼下坡路面以15 ~20 km/h 的速度熄火空挡滑行.同时,专业评审团随车进行减振器异响的评价,并测量车内乘员的右耳噪声和减振器活塞杆顶端振动加速度信号,采样频率分别为44 100、2 048 Hz,分辨率为1 Hz,试验示意如图1 所示.
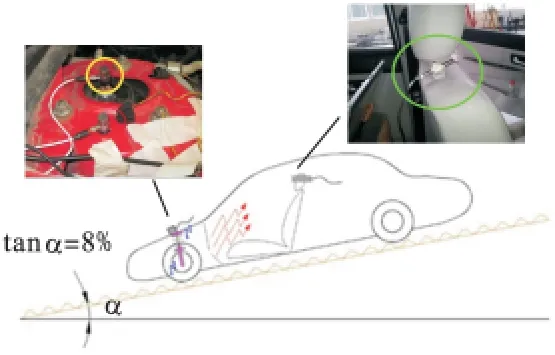
图1 减振器整车道路试验示意Fig.1 Schematic diagram of shock absorber in the vehicle road test
常用的噪声评价方法主要有等级评分法和成对比较法.等级评分法根据减振器异响的程度,确定不同的评分等级,将评价人员的全部评分加和求平均的值作为评价指标,其关键是评分刻度的确定.由于减振器异响的特殊性,评价选择3 分制的等级评分法. 将减振器异响分为严重异响(评价1 分)、轻微异响(评价2 分)和无异响(评价3 分)3 类,由专业评审团进行评分. 图2 为减振器活塞杆顶端振动加速度频谱曲线.由图2(a)可知,严重异响减振器的频谱曲线在300 ~500 Hz 范围内幅值最大,轻微异响件次之,无异响件最小,由此可知,减振器异响的强弱可由减振器活塞杆顶端振动加速度信号来刻画.
1.2 减振器台架试验与整车试验的一致性规律
减振器整车试验的目的是获得减振器异响主观评价,但其存在一致性和可重复性较差的缺点.为了获得具有统计意义上的结果,并且节约大量的时间和成本,进行了减振器台架试验,图3 为减振器台架试验示意. 为了模拟减振器的实际工作状况,减振器在台架上的安装方式与整车相同,并且通过迭代加载实际的路谱作为激振信号,同时采集减振器活塞杆顶端和台架作动头的振动加速度信号,采样设置同减振器整车试验.
比较图2(a)、(b)可见,3 种异响程度的减振器样件都在300 ~500 Hz 范围内有较好的区分度,其中严重异响件的频谱曲线明显高于轻微异响件与无异响件,由此可知,减振器异响对于整车试验与台架试验具有一致性规律,即可用台架试验代替整车试验对减振器异响进行鉴别.
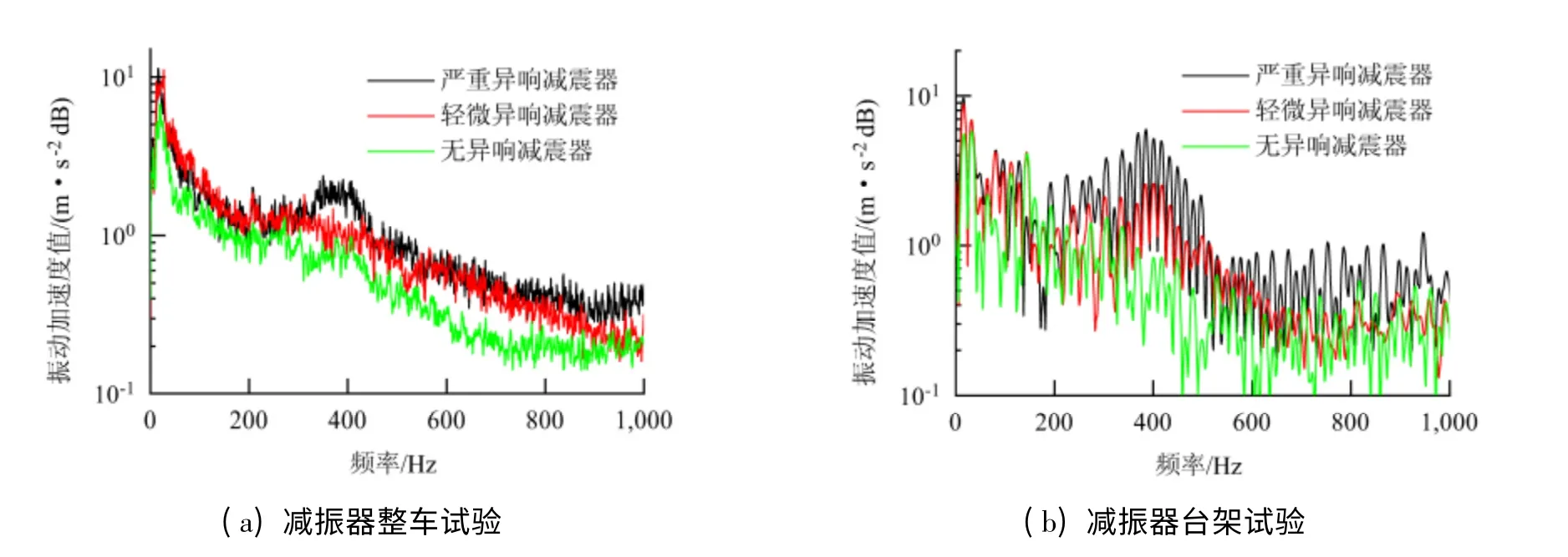
图2 减振器活塞杆顶端振动加速度频谱Fig.2 Spectra of piston rod vibration acceleration
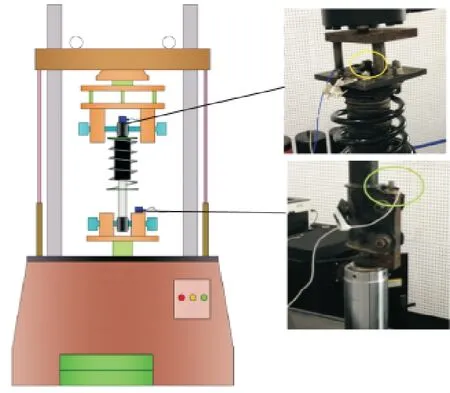
图3 减振器台架试验示意图Fig.3 Schematic diagram for shock absorber test rig
2 基于深度学习的减振器异响鉴别
2.1 深度学习模型选取及数据样本采集与预处理
深度学习是机器学习(machine learning)当中的一个新领域[12],深度学习有两大经典模型:深度信念网络(deep belief networks,DBNs)与卷积神经网络(convolutional neural networks,CNNs). 其中,深度信念网络的研究和应用最为广泛,也是本文所采取的方法,具体理论与方法见文献[12-17].
减振器异响的鉴别首先采集样本并建立样本数据库.对经过整车试验的130 支减振器(严重异响件21 支,轻微异响件31 支,无异响件78 支)分别进行台架试验,收集减振器活塞杆顶端振动加速度信号与台架作动头激励信号,其中,减振器活塞杆顶端加速度信号作为异响鉴别的原始数据,台架作动头激励信号作为后期调整活塞杆顶端加速度信号相位差的辅助信号. 根据深度信念网络理论[12]可知,样本的预训练是一个无监督的特征提取过程,在这样的条件下适当增加样本的数目可以更好地提取出减振器异响的本质特征,所以对进行台架试验的每一只减振器分别采集10 组信号,每次采集时间为1 s,所采集的这10 组信号评价与其在整车路试中评价得分相同. 然后,根据台架作动头激励信号作为修正相位差的辅助信号,将活塞杆顶端振动加速度信号截断为同触发激励,同相位,长度约为0.2 s(400 个采样点)的振动信号. 由于深度信念最后的输出为样本的联合概率分布,其值在[0,1]之间,需要对输入的样本进行标准化处理,按式(1)对样本数据进行[0,1]归一化处理.这样,样本数据库由1 300 个长度为400 个点的归一化减振器活塞杆顶端加速度信号组建而成.

式中:Xi为样本数据;
Xmin、Xmax分别为样本数据的最小值与最大值;
2.2 基于DBNs 的减振器异响鉴别模型
根据深度信念网络的理论可知,样本的输入数据为传感器收集的信号,为了使结果具有一般性,从样本数据库中随机选取训练数据和测试数据,并进行深度信念网络的建模,具体步骤如下:
(1)样本的选取
构建模型的训练样本集{(Xi,Yi)}与测试集{(Xj,Yj)},其中:Xi为从样本数据库中随机抽取的1 000 个样本;Xj为剩下的300 个样本;Yi、Yj分别为每个样本对应的评价得分.
(2)DBNs 的建立
DBNs 由多个玻尔兹曼机(restricted Boltzmann machine,RBM)堆积而成,由于采用“逐层贪婪训练方法”进行网络的训练,则计算复杂度是线性的,并且DBNs 的深度越深,对原始数据的表达就越抽象.根据数据量的规模和网络复杂度的影响,将3 个玻尔兹曼机堆积形成的DBNs 作为深度学习模型,如图4 所示,图中:可见层V 的输入是训练样本集;h1、h2、h3分别表示第1、第2、第3 隐含层;W 为相邻的两层神经元连接权值,并且相邻两层神经元与其连接权值构成一个玻尔兹曼机.
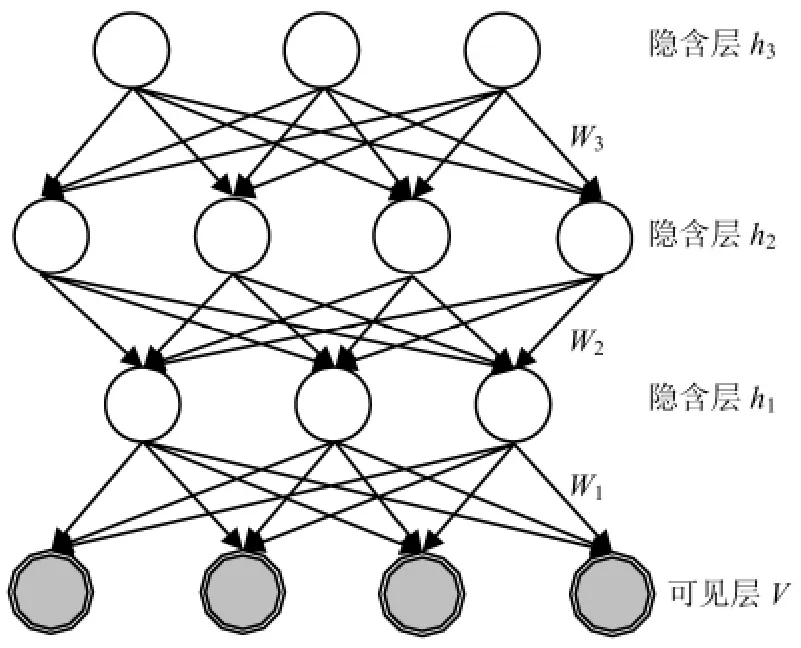
图4 深度信念网络拓扑结构Fig.4 Topology of DBNs
由于每一个输入样本的长度是400 个点,即样本为400 维,将可见层V 的神经元个数取为nV=400.隐含层神经元的个数关系到DBNs 的训练速度与准确度,特别是最顶层的隐含层直接关系到最终的鉴别准确率.但对于隐含层神经元个数的选取尚无理论上的指导,也没有统一的经验公式,据目前大量试验经验来看,可取nh1=300、nh2=200、nh3取[50,55,…,150]其中之一,因为原始样本含有大量的噪声信号,而每一个隐含层又是原始样本的另外一种表达,逐渐减少隐含层神经元个数的目的就是为了能将减振器异响的主要特征信息逐步提取出来.RBM 重构特征与原始信号的误差用“重构误差”来表示,“重构误差”是根据RBM 的分布进行一次吉布斯采样后所得到的新特征与原始数据的差异,可用式(2)来表示. 重构误差能在一定程度上反映RBM 对输入数据的似然度.

式中:v 为原始数据;
T 为进行重构的迭代次数.
图5 为训练数据的重构误差曲线,可见当nh3取110 时,重构误差最小,因此,最终建立的DBNs的拓扑结构为400-300-200-110.
(3)DBNs 的训练
使用的DBNs 模型是在Hinton 所构建的框架[11]下 经 过 次 修 改 而 成,运 行 环 境 为MATLAB2013b.在进行模型训练之前,需要对模型各参数进行初始化,由于DBNs 可调参数过多,本文仅列出主要参数的设置. DBNs 的主要可调参数有:RBM 学习率、动量项、RBM 初始权重与偏置、RBM 小批量数据容量、RBM 重构迭代次数、DBNs微调次数以及每一层神经单元数目.
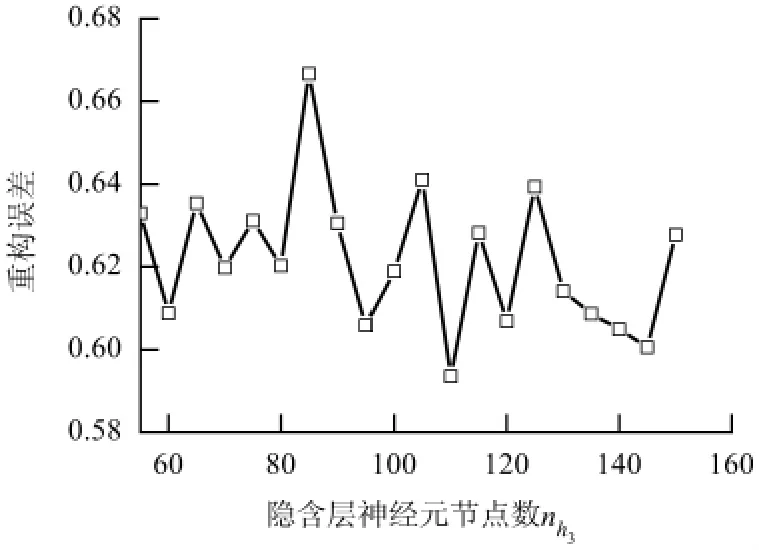
图5 训练样本重构误差随nh 3 节点数目变化曲线Fig.5 Change of training sample reconstruction error with node number nh 3
RBM 学习率包括权值学习率lw,可见层偏置学习率lbv以及隐含层偏置学习率lbh,学习率过大,将导致重构误差急剧增加,权重会变得很大,一般取0.005 ~0.200 之间,这里令lw=0.050,lbv=0.100,lbh=0.100.为了弥补学习率过大或过小带来的问题,引入了动量项,该项可使本次参数更新的方向不完全由当前的梯度方向决定,还结合了上一次参数的更新方向,在某些情况下,可以避免算法在早期陷入局部极值.更新公式为

式中:m 为动量项,在迭代初期令m=0.5,中后期令m=0.9;
wij为可见层单元与隐含层单元的连接权值;
t 为迭代次数.
一般地,连接权重可初始化为正态分布N ~(0,0.1)上的随机数,可见层单元偏置bi和隐含层单元偏置bj初始化为0.
RBM 使用对比散度[15]进行权重与偏置的更新,若每次基于全部训练样本进行,则整体计算量很大,将训练集和测试集事先分为若干个“小份”,采用分块的方式来学习可加快计算速度,现将训练集和测试集设为50 个样本一份进行分块计算.RBM 进行1 次权值更新即迭代1 次,设置每层RBM 迭代的次数为100 次.RBM 权值更新完毕后,DBNs 进入微调学习阶段,微调是一种监督学习的过程,利用反向传播算法对整个网络的权值进行更新,这样在每一次迭代中,网络中所有的权重值都可被进一步优化,并且用交叉熵[11]来衡量输入和输出概率分布的相似性,交叉熵的定义为
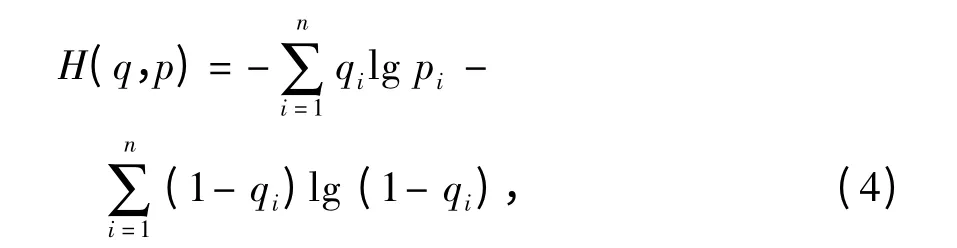
式中:q、p 分别为输入和重构样本的概率分布;H(q,p)为交叉熵.
由式(4)可知,交叉熵的值越小,重构的概率分布越接近输入的概率分布,则隐含层提取的特征越近似原始输入数据的特征,这里设置DBNs 的微调次数为200 次. 由于每一层神经元的数目在DBNs 建模时已确定,之后可在设置好的参数下对DBNs 进行训练,所得的交叉熵曲线如图6 所示.
从图6 可以看出,在微调达到140 次以后,交叉熵的值基本趋于稳定,表明输出特征已经是原始数据的另外一种表达.

图6 原始数据逐级特征提取曲线Fig.6 Layer-wise feature extraction curve of original data
图7 为原始数据DBNs 逐级特征提取曲线,图中纵坐标为隐含层重构特征.
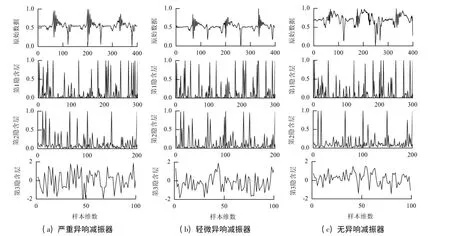
图7 原始数据DBNs 逐级特征提取曲线Fig.7 Layer-wise feature extraction curve of original data in DBNs
由图7 可知:(1)随着隐含层深度的增加,提取的减振器异响特征越来越抽象;(2)严重异响减振器的第3 隐含层重构特征比轻微异响减振器第3 隐含层重构特征粗糙,即数据信息变化快速、陡峭,并且轻微异响减振器的第3 隐含层重构特征又比无异响减振器的粗糙,这是由于第3 隐含层数据点中包含了减振器异响的细节信息.最终得到的第3 隐含层重构特征就是原始减振器活塞杆顶端振动加速度信号在低维新空间中的特征表达,并且模型将以此作为减振器异响鉴别的基础.
2.3 分析结果与对比
利用上述建立好的深度信念网络模型对样本数据库中的测试数据进行鉴别,为了减少随机选取样本所带来的误差,计算结果取程序运行10 次后的平均值. 图8 为测试集误判样本个数曲线. 由图8 可知,在微调200 次时,测试样本最终的误判数为10 个,并将此结果与经过参数优化的BP 神经网络、支持向量机及文献[1-5]中所提的方法进行比较,结果见表1. 表1 中:训练集中,严重异响件样本149 个,轻微异响件样本263 个,无异响件样本588 个;测试集中在严重异响件样本59 个,轻微异响件样本66 个,无异响件样本175 个.
由表1 可见,在输入仅为减振器活塞杆顶端振动加速度信号原始数据的条件下,深度信念网络模型的异响鉴别准确率达96.7%,并且对于每类异响减振器都有较高的鉴别准确度,而BP 神经网络和支持向量机模型的鉴别结果不理想.这主要是因为深度信念网络通过对输入数据逐级提取从底层到高层的特征,能很好的建立从底层信号到高层特征的映射关系,从而能有效地对减振器异响进行鉴别.然而原始数据的维数较高并且含有大量的噪声信号,BP 神经网络和支持向量机很难从中提取出异响的主要特征信息,导致辨识准确度不高. 作为人工特征提取的方法,时域峰值衰减量计算简单、方便,但鉴别准确率受外界干扰敏感,辨识准确度不高;功率谱均方根值法从频域的角度对减振器异响信息进行了提取,取得了一定的效果,但鉴别准确率仍不理想;小波特征能量法把焦点集中在减振器活塞杆顶端换向冲击的瞬间,提取出了异响的主要特征信息,鉴别准确率较高. 以上3 种人工特征提取方法的鉴别效果都不及深度信念网络方法,然而,由于深度信念网络模型隐含层较多,所以运行时间相对较长.
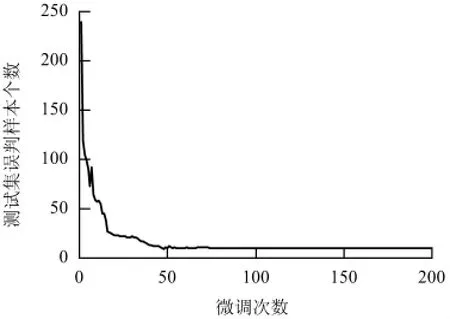
图8 测试集误判样本个数曲线Fig.8 Curve of misclassified sample number in the test set

表1 6 种方法鉴别效果对比Tab.1 Comparison of identification results of the six methods
3 结 论
以深度信念网络为基础,建立了减振器异响鉴别模型,该模型训练只需要减振器活塞杆顶端振动加速度信号作为输入,无需进行人工特征提取,便能逐级提取原始信号当中的有用信息,并且可以较好的适应各种不同的样本分布,实现了较为一般意义上的异响鉴别. 分析结果表明,当原始信号维数较高且含有大量噪声的情况下,BP 神经网络和支持向量机模型效果欠佳,但深度信念网络模型仍然能够获得很高的减振器异响鉴别准确率,并且比传统的人工特征提取方法效果好,说明了其可行性与实用性.由于该方法具有抗干扰能力强和鉴别准确率高的优点,可为今后大批量、不同型号减振器异响鉴别以及提高鉴别准确度提供新途径,具有广泛的工程应用前景.
致谢:西南交通大学研究生创新实验实践项目基金资助(YC201402104).
[1] 舒红宇,王立勇,吴碧华,等. 液力减振器结构异响发生的微过程分析[J]. 振动工程学报,2005,18(3):
282-287.SHU Hongyu,WANG Liyong,WU Bihua,et al.Analysis on the abnormal structure noise yielding processofhydraulic shock absorber[J]. Journal of Vibration Engineering,2005,18(3):282-287.
[2] BENAZIZ M,NACIVET S,DEAK J,et al. Double tube shock absorber model for noise and vibration analysis[J]. SAE International Journal of Passenger Cars Mechanical Systems,2013,6(2):1177-1185.
[3] 宋睿. 汽车双筒式减振器异响的产生机理与控制方法研究[D]. 成都:西南交通大学,2012.
[4] 么鸣涛,顾亮,管继富. 双筒式减振器异响试验分析[J]. 工程设计学报,2010,17(3):229-235.YAO Mingtao,GU Liang,GUAN Jifu. Test analysis on the noise of automobile shock absorber[J]. Journal of Engineering Design,2010,17(3):229-235.
[5] 丁渭平. 汽车底盘系统NVH 及异响控制技术研究[C]∥汽车NVH 控制技术国际研讨会. 成都:[s.n.],2013:93-106.
[6] 黄海波,李人宪,丁渭平,等. 基于台架试验的悬架减振器异响辨识研究[J]. 振动与冲击,2015,34(2):191-196.HUANG Haibo,LI Renxian,DING Weiping,et al. Rig test for identifying abnormal noise of suspension shock absorber[J]. Journal of Vibration and Shock,2015,34(2):191-196.
[7] 余凯,贾磊,陈雨强,等. 深度学习的昨天、今天和明天[J]. 计算机研究与发展,2013,50(9):1799-1804.YU Kai,JIA Lei,CHEN Yuqiang,et al. Deep learning:yesterday,today,and tomorrow[J]. Journal of Computer Research and Development,2013,50(9):1799-1804.
[8] 张建平,胡明华,吴振亚,等. 基于BP 网络的空中交通管制运行品质评价[J]. 西南交通大学学报,2013,48(3):553-558.ZHANG Jianping,HU Minghua,WU Zhenya,et al.An improved integrated evaluation method on operation performance of air traffic control based on BP network[J]. Journal of Southwest Jiaotong University,2013,48(3):553-558.
[9] 吴志周,范宇杰,马万经. 基于灰色神经网络的点速度预测模型[J]. 西南交通大学学报,2012,47(2):285-290.WU Zhizhou,FAN Yujue,MA Wanjing. Spot speed prediction model based on grey neural network[J].Journal of Southwest Jiaotong University,2012,47(2):285-290.
[10] YOON J,YANG I,JEONG J,et al. Reliability improvement of a sound quality index for a vehicle HVAC systemusing a regression and neural network model[J]. Applied Acoustics,2012,73:1099-1103.
[11] 秦娜,金炜东,黄进,等. 基于EEMD 样本熵的高速列车转向架故障特征提取[J]. 西南交通大学学报,2014,49(1):27-32.QIN Na,JIN Weidong,HUANG Jin,et al. Feature extraction of high speed train bogie based on ensemble empirical mode decomposition and sample entropy[J].Journal of Southwest Jiaotong University,2014,49(1):27-32.
[12] HINTON G E,SALAKHUTDINOV R. Reducing the dimensionality of data with neural network[J].Science,2006,313:504-507.
[13] BENGIO Y. Learning deep architectures for AI[J].Foundations and Trends in Machine Learning,2009,2(1):1-127.
[14] AREL I,ROSE D C,KARNOWSKI T P. Deep machine learning: a new frontier in artificial intelligence research[J]. IEEE Computational Intelligence Magazine,2010,5(4):13-18.
[15] HINTON G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation,2002,14(8):1771-1880.
[16] GRAVES A,MOHAMED A R,HINTON G E. Speech recognition with deep recurrent neura inetworks[C]∥Acoustics,Speech and Signal Processing (ICASSP),IEEE International Conference. Santa Clara:[s. n.]2013:6645-6649.
[17] HINTON G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation,2002,14(8):1771-1880.

