一种基于裁剪FP-Tree 的频繁项集挖掘算法

罗 芳

(宁德师范学院 计算机系，福建 宁德 352100)

关联规则挖掘是数据挖掘技术的重要内容之一，在金融、教育、销售等行业得到了越来越广泛的应用。在Apriori 算法［1，2］被AgrawalR 等人提出以后，许多学者对其进行了改进，如FP－Growth［3］，它比Apriori 算法快一个数量级。FP－Growth 算法通过建立FP 树来挖掘数据库中频繁项集。首先扫描一次数据库，算出各项集的支持度计数，通过与用户设定的最小支持度计数相比，得出频繁1－项集，对频繁1－项集按支持度计数进行从大到小排序插入频繁项头表中;其次，再扫描一次数据库，删除数据库中非频繁1－项集的元素，构造FP 树，并挖掘出频繁k(k ＞1)－项集。FP－Growth 算法在挖掘过程中，需要产生条件FP 树，当最小支持度较小时，将产生大量的条件FP 树，占用的存储空间会非常庞大。由于FP 树和条件FP 树都需要自顶向下、自底向上两次遍历，遍历占用时间也大大增加。

针对FP－Growth 算法的不足之处，吴倩等提出了压缩FP－tree 的改进搜索算法，［4］张中平等提出了基于矩阵的频繁项集挖掘算法，［5］王利钢等提出了基于FP－tree 的项约束关联规则挖掘算法，［6］宋威等提出了基于动态裁剪频繁模式树的频繁项集并发挖掘算法，［7］郭伟等提出了基于数组的FP－tree 频繁项集挖掘算法，［8］付冬梅等提出了基于FP－tree 和约束概念格的关联规则挖掘算法及应用研究。［9］其中文献［7］裁剪FP 树的方法存在缺陷，可能会误删树中结点，导致挖掘出的频繁项集不正确。为此本文提出了一种新的基于数组的频繁模式树裁剪算法PruneFP－tree(简称F_ FP)，利用数组存储所有的2－项集的支持度计数，对FP 树中的叶子结点进行有效裁剪，减少条件FP 树的生成，减少算法的递归次数。

1 理论基础

数据库D 是事务T 的集合，事务T 项目I 的集合，T I。若X T，则X 为一个项集，X 的支持度计数为包含X 的事务总数，如果X 的支持度计数大于用户给定的最小支持度计数，则X 为频繁项集。

(1)FP－tree 的树结构:

FP－tree 包含一个值为null 的根结点、一棵项前缀子树和一个频繁项头表HTable。树中每个结点包括5 个域:item_ name、count、node_ link、child_ link、parent_ link，count 为支持度计数，node_ link 指向下一个具有相同item_ name 的结点，child_ link 指向子结点，parent_ link 指向父结点。频繁项头表表示为Head_ table，其中每个表项 包 括 2 个 域: item_ name、 node_ link，item_ name 的指针node_ link 指向FP－tree 中与之同名的第1 个结点。

(2)数组A 的定义如下:

I = {I1，I2，…，In}是HTable 频繁项表头中项的集合，A 是一个长度不大于n－1 的结构数组，用于存放2－项集的支持度计数，数组元素的值可表示为:count(Ii，Ij)，其中count(Ii，Ij)是2－项集的支持度计数。如果2－项集{Ii，Ij}的支持度计数为2 则A［i，j］= 2 、A［i，j］= 2 ，只取前一项来记录即可，因此可知(i ＜j)。

定理1 当一棵FP－tree 构造完成以后，树中i 结点的分布不会发生任何变化，i 条件模式不变。

证明:设FP 树中i 结点的集合为{N1，N2，…，Nm}。当FP 构造完以后不会有新节点加入，则其节点条件模式不变。

定理2 若一个项集X 的子集不是频繁项集，那么项集X 也不是频繁项集。

证明:设k－项集X 为{I1，I2，…，Ik}，如果存在它的任意子集{I1，I2，…，Ip}(1 ＜p ＜k)不是频繁项集，则它的支持度计数(同时出现的次数)小于最小支持度计数，显然{I1，I2，…，Ik}同时的支持度计数也小于最小支持度计数，则项集X 也不是频繁项集。

定理3 设FP 树中结点i 为叶子结点，存在前缀路径B = {B1，B2，…，Bk}，如果包含结点i 的项集X 在FP 树中Bk上是非频繁的，且(B1∪i)∪(B1∪i)，…，(Bk∪i)中也找不到包含i 的频繁项集X，则可以在树中删除该路径上的结点i。

证明:如果项集X 在某条路径上是非频繁的，说明在该路径上找不到频繁项集X，若在(B1∪i)∪(B1∪i)，…，(Bk∪i)中也找不到频繁项集X，则说明在FP 树中找不到包含i 的频繁项集X。说明可以从树中删除该路径的叶子结点i。根据定理2 结合FP 树的特点(FP 树是由频繁1－项集构建的)，只需要求出结点i 的前缀路径上的各结点与结点i 组合成的2－项集在该FP 树中是不是频繁的，如果不是，则说明以该2－项集为子集的项集都不是频繁的。

定理4 若在某路径上，结点i 的父亲结点为根结点NULL，且孩子结点为空，则可删除该路径的结点i。

证明:若结点i 的父亲结点为根结点NULL，且孩子结点为空，不可能找到包含i 频繁k(k ＞1)－ 项集，所以可以删除该路径的结点i。

2 F_ FP 算法

(1)首先扫描数据库，算出各1－项集的支持度计数，过滤非频繁1－项集，将HTable 中的结点顺序按支持度计数从大到小排序。对HTable 表中的事务进行排序。

(2)再扫描数据库，构造存放2－项集的数组A，并构造FP 树(与FP－Growth 算法一致，因此不详细展开描述)，裁剪FP 树。

(3)裁剪FP 树的过程:①若树中某路径上结点i 的父结点和孩子结点都为空，则删除该结点;②若树中某路径上的结点i 的孩子结点为空，且在该路径上没有包含i 的频繁2－项集，则要再寻找整棵树种是否存在包含i 的频繁2－项集，如果未找到，那么删除该结点。

输入为数据库DB，最小支持度计数min_ sup，输出FP 树。

(1)count(n)←0;

(2)foreachTiinDB //计算1－项集支持度计数

(3)foreachIiinTi

(4) {生成HTable 表，将事务Ii按支持度计数从大到小排列;

(5)［p/P］= sort(Ti，Item_ sets);}

(6)A［n－1，n－1］←0;//初始二维化数组

(7)T ←null;//根结点为null

(8)foreachIiinFrequent_ Items

(9)foreachIjinTi

(10){A［i，j］++;//构造数组(i ＜j)

(11)insert_ tree(［p/P］，T);}//构造FP 树

(12)prune_ tree(T);//裁剪FP 树

prune_ tree(T)函数如下:

(1)foreachiinHTable

(2){if(i 的孩子为空且父亲为根结点null)then 删除结点i;

(3)if(i 的孩子为空且i 的前缀路径上找不到包含i 的频繁2－项集)then

(4){foreachj ∈Bj

if(A［i，j］＜min_ sup)then 删除结点i;}}

3 算法示例

事务数据库列表如表1 所示，设最小支持度计数为3。

表1 事务数据库表

(1)扫描数据库，找出1－项集{a，b，c，d，e，f}的支持度计数为:{5，6，6，5，3，2}。由于f 支持度计数为2 则1－项集{f}是非频繁的，将频繁1－项集按支持度计数从大到小排:{b，c，a，d，e}，将数据库事务也按该顺序调整，如表1 的Frequent_ Items。

(2)再次扫描已排序的数据库，构造数组A。首先读取Frequent_ Items 中排好序的T1，得到A［b，c］= 1、A［b，d］= 1、A［c，d］= 1;读取T2:A［b，a］= 1;读取T3:A［c，a］= 1、A［c，e］= 1、A［a，e］=1;读取T4:A［b，c］=1+1 =2、A［b，d］= 1 +1 = 2、A［b，e］= 1、A［c，d］= 1 + 1 = 2、A［c，e］= 1 +1 = 2、A［d，e］= 1;依次扫描剩余事务可得到如下数组A 如图1 所示:

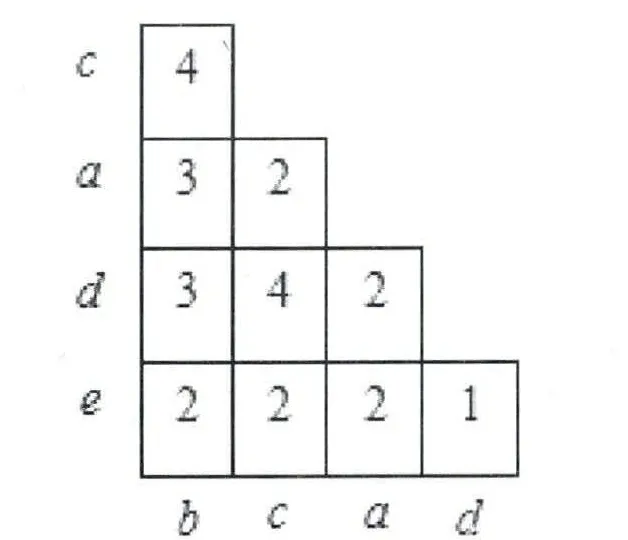
图1 数组A

(3)首先创建FP 树的根结点，对排序的事务按顺序调用insert_ tree(［p/P］，T)，如果i 是p 的孩子，则树中p 结点数加1，否则把i 作为新的结点加入树中，递归调用insert_ tree(［p/P］，T)，构造FP 树如图2 所示。

图2 构造FP 树

(4)对树FP 进行裁剪。

首先求出e 的模式基:(c，a:1)、(b，c，d:1)、(b，a:1)，这三条前缀路径上都不包含e 的频繁项集，再查找数组可知:A［e，b］ = 2 、A［e，c］ = 2 、A［e，a］= 2 、A［e，d］= 2 ，说明在整棵树种找不到含e 的频繁2－项集，根据定理3 则可删除如图1 所示①处的所有e 结点;求出d 的模式基:(b，c，a:1)、(b，c:2)、(a:1)、(c:1)，这四条前缀路径上都不包含d 的频繁2－项集，查找数组可知:A［d，b］= 3 、A［d，c］= 4 、A［d，a］= 2 ，说明在整棵树中找到包含d 频繁2－项集{{b，d}，{c，d}}，则前缀路径(b，c，a:1)、(b，c:2)、(c:1)上的结点d 不能删除，前缀路径(a:1)上的结点d 可以删除，如图1 的②处所示;求出a 的模式基:(b，c:1)、(b:2)、(c:1)，这四条前缀路径上都不包含a 的频繁2－项集，查找数组可知:A［a，b］=3 、A［a，c］= 2 ，说明在整棵树中找到包含a 频繁2－项集{a，b}，则将前缀路径(c:1)上的结点a删除，在寻找模式基的时候发现如图1 中左③所示的结点a 的父亲结点为根结点，且a 又是个叶子结点，根据定理4 可删除该结点;c、b 都不是叶子结点，则裁剪结束。裁剪后的FP 树如图3 所示:

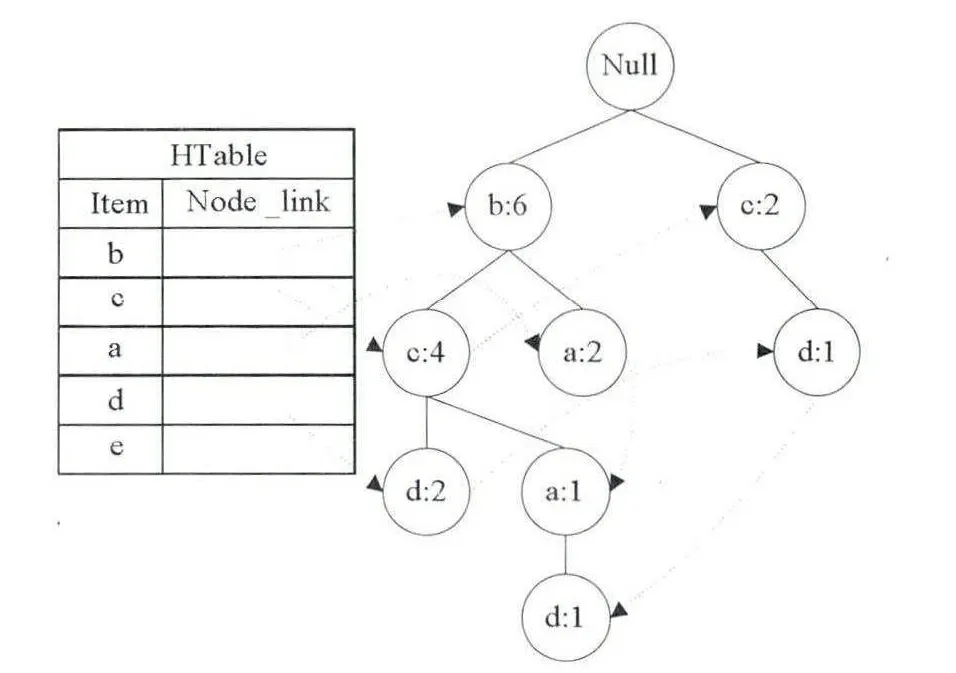
图3 裁剪后的FP 树

4 实验结果与分析

实验采用数据集Connect 进行实验，分析数据源的大小为16.0MB，事务数为240112 条，项数为232 个。算法编程语言采用C+ +，实验环境为:处理器为Intel (R)Core (TM)i7－5500，运算速度是2.40GHz，内存(RAM)为8GB，64 位WIN7 操作系统。两种算法在最小支持度为0.1、0.25、0.5、1、1.5 时，最小支持度与执行时间的关系如图4 所示，随着最小支持度的升高两种算法的执行时间大幅度减少，显然，在相同的条件下，由于对FP 树进行有效裁剪，生成的条件FP 树也大大减少，减少了递归调用条件FP 树的时间，相比FP－Growth算法，改进后的算法执行时间效率优势明显。

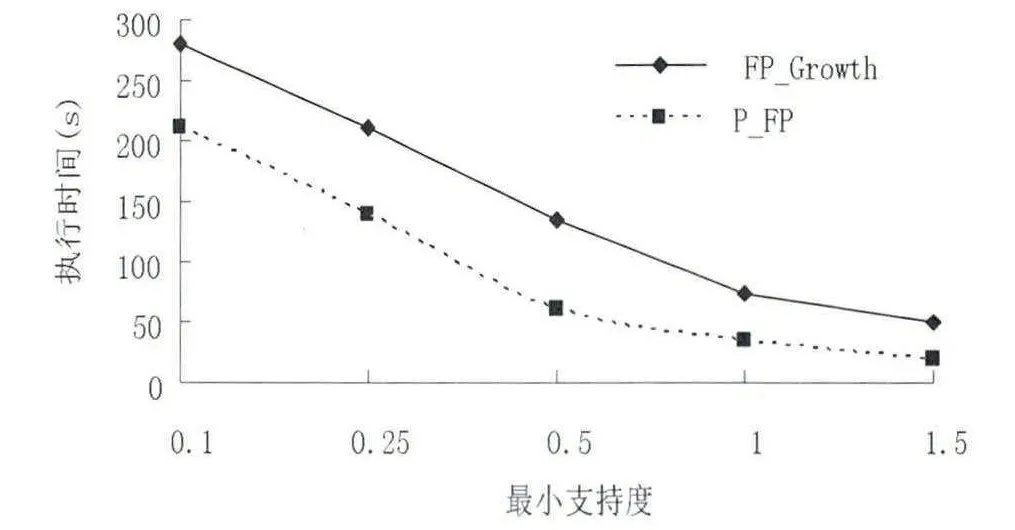
图4 P_ FP 算法和FP－Growth 算法执行时效比较

在输入数据集相同的情况下，P_ FP 算法和FP－Growth 算法中与FP 树的结点个数与事务数之间的关系如图5 所示，可以看出:输入事务数越多，改进后的P_ FP 算法生成的结点个数和FP－Growth 算法相比，差距越大，说明生成的条件FP树越少，算法执行效率越高。随着事务数的增多，改进后的P_ FP 算法和FP－Growth 算法相比生成的结点个数减少了1 倍以上。

图5 P_ FP 算法和FP－Growth 算法的结点数比较

5 结束语

FP－Growth 算法在执行过程中生成大量的条件FP 树，遍历这些条件FP 树的时空消耗的过大，为了解决这个问题，本文提出了一种基于数组的FP 树裁剪方法，利用“若某一项集的子集是非频繁的，那么该项集一定不是频繁项集”这一性质来对要裁剪的结点进行筛选，有效减少了条件FP树的生成，提高算法挖掘效率，实验结果证明P_FP 算法的可行性和有效性。

［1］ Agrawal R，Imielinski T，Swami A.Mining Association Rules between Sets of Items in Large Databases［C］.In:Proc of the ACM SIGMOD International conference on Management of Data，Washington DC，1993:207－216.

［2］Agrawal R，Srikant R.Fast algorithms for mining association rules［A］.Proc.1994 Int’l Conf.Very LargeData Bases (VLDB’94)［C］.Santiago，1994:487－499.

［3］HAN J，PEI J，YIN Y，etal.Mining frequent patterns without candidate generation a frequent_pattern tree approach［J］.Data Mining and Knowledge Discovery，2004，8(1):53－87.

［4］吴倩，罗健旭. 压缩FP－tree 的改进搜索算法［J］. 计算机工程与设计，2015，36(7):1771－1777.

［5］张中平，李岩，杨静. 基于矩阵的频繁项集挖掘算法［J］. 计算机工程，2009，35(1):84－86.

［6］王利钢，陈平，胡松. 基于FP－tree 的项约束关联规则挖掘算法［J］. 信息化研究，2014，40(6):11－15.

［7］宋威，刘文博，李晋宏. 基于动态裁剪频繁模式树的频繁项集并发挖掘算法［J］，山东大学学报，2011，41(4):49－55.

［8］郭伟，叶德谦. 改进的基于FP－tree 频繁项集挖掘算法［J］. 计算机工程与应用，2007，43(19):174－176.

［9］付冬梅，王志强. 基于FP－tree 和约束概念格的关联规则挖掘算法及应用研究［J］. 计算机应用研究，2014，31(4):1013－1016.