基于图像复杂度的图像分割算法

王 崴，王晓军，刘晓卫，周 诚

（1.西安交通大学机械制造系统工程国家重点实验室，陕西 西安 710049；2.空军工程大学防空反导学院，陕西 西安 710051）

0 引言

图像分割是图像处理与计算机视觉领域低层次视觉中最为重要和基础的领域之一，图像分割结果的好坏将直接影响到后续的视觉分析和模式识别工作。阈值法作为一种传统的图像分割方法，因其实现简单、计算量小、性能稳定的特点，一直是图像分割领域最基本和应用最为广泛的分割算法［1］。阈值选择是否合适决定着最终图像分割的质量。

经典的基于阈值的图像分割算法，一直是以灰度直方图作为阈值选取的依据。但对于文献［2］中提出的“如果两幅不同的图像具有相同的灰度分布，从而得到相同的门限，该方法是不是同时适用于两幅图像呢？［2］”问题，以灰度直方图为依据的阈值选取算法，无法给出解答。研究人员尝试找到一种更加全面的灰度描述，来作为阈值选取的依据。香农（Claude Shannon）信息熵（Entropy）的概念开始逐渐引起研究人员的关注。结合信息熵概念的图像描述方法成为一个热点。文献［3］提出了二维灰度直方图熵的概念［3］。文献［4］采用图像方差加权信息熵来反映图像的复杂度特征，对低信噪比的红外云层背景弱小目标图像取得了良好的检测效果［4］。文献［5］提出用灰度-信息量直方图来表征图像的特征，完成对图像的分割［5］。

但无论是经典的阈值分割算法，还是上述文献中以信息熵为基础的改进图像描述方法，只是从不同方面对图像中的各灰度级进行了统计，都不能准确反映图像中各灰度级的空间分布情况，并且对于待分割区域与背景具有相近灰度级的图像存在欠分割现象。本文针对此问题，提出了基于图像复杂度的图像分割算法。

1 图像复杂度

图像复杂度（Image Complexity）是对图像内在复杂程度的描述，它能反映图像完成某些操作（如边缘检测、图像增强、图像压缩、目标自动提取等）的内在的困难程度［6］。图像复杂度的定量计算来源于广义集合内部复杂度的计算公式。

广义集合的内部复杂度的计算公式：

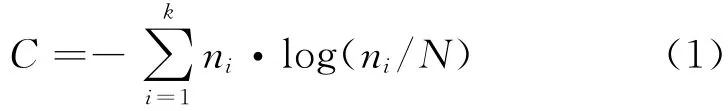
式（1）中C 表示复杂度，k表示广义集合内不同标志值的个数，ni表示标志值，i表示占有的个体数量，N 表示个体总量。如果对数运算中取以2为底的对数所求得的复杂度的单位为比特（Bite），若以e为底则所求得的复杂度单位是奈特（Nat），若以10为底，则所求得的复杂度单位为哈特莱（Hartly）［7］。

针对数字图像这一特定对象来说，本文引入信息熵（Comentropy）概念。信息熵：可以反映图像灰度级的个数以及各个灰度级出现的情况［8］。信息熵的计算公式由式（1）演化为：

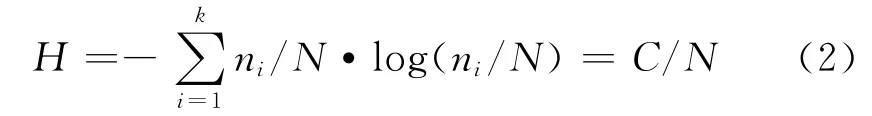
上述信息熵的计算公式与数字图像的灰度直方图有着密切的联系。灰度直方图反映图像中各灰度级出现的频率，所以可以得到计算公式中的ni和ni／N 。但信息熵同样不能反映图像中各灰度值的空间分布情况，无法满足对本文对图像复杂度的要求。

为了反映数字图像灰度值的空间分布情况引入灰度共生矩阵。灰度共生矩阵（Gray Level Cooccurrence Matrix，简称GLCM ）是一种用来分析图像纹理特征的重要方法，它建立在估计图像的二阶组合条件概率密度函数的基础上，通过计算图像中有一定距离和一定方向的两个像素之间的灰度相关性，对图像的所有像素进行调查统计［9］。GLCM 可以综合描述灰度的分布情况和反应图像的复杂度。

在空间三维坐标系Oxyz 所表示的坐标区域内，设Oxy 平面内各点对应图像各像素所在位置，z轴表示各像素点的灰度值。则在GLCM 中第i行、第j列元素Pij表示：从灰度值为i的像素点位置出发，距离为（dx，dy）的另一像素点位置上出现灰度值为j的频度，其空间位置关系如图1所示。

图1 空间位置关系Fig.1 Spatial location relationship

元素Pij的数学表达式为：

式中，x的取值范围为（0，m-1），m 表示图像在x 轴方向上像素总数，y 的取值范围为0，n -（ ）1 ，n表示图像在y 轴方向上像素点的总数。dx，dy表示位置偏移量，具有一定的方向性。θ为灰度共生矩阵的生成方向，θ可以取0°、45°、90°、135°这四个方向。

归一化处理后得出Q（i，j）=P（i，j，d，θ）／R 其中R，表示归一化常数。

为了能够定量的度量图像的复杂度，需对灰度共生矩阵进行特征参数计算。其中具有典型度量特征的参数有：

1）能量：对图像灰度分布均匀性的度量，也可以在一定程度上反应图像中纹理的粗细程度［10］。

不难证明，图像灰度值分布越均匀则能量越小，灰度值分布越凌乱则能量值越大。

2）对比度也称反差：可以反映图像纹理的清晰程度，也可以在一定程度上反映出进行图像目标分割的难易程度［11］。

图像对比度越大，则图像的视觉效果越清晰，图像纹理沟壑越深，反之对比度越小，图像的效果越差，感觉越模糊。

3）相关度

相关性数值的大小反映了图像中局部灰度相关性。它可以用来度量灰度共生矩阵元素的分散非均匀程度或者图像的复杂度，是衡量图像复杂度大小的一个有效指标［12］。

根据图像的信息熵和图像的灰度共生矩阵特征参数对图像复杂度影响的大小程度，引入权值，并进行加权求和。所求得的图像复杂度数值能较为客观反应图像的复杂程度和进行图像分割的难易程度，其中信息熵、对比度的权值我们定为1，相关度与能量的权值定为-1。所以图像复杂度Ωk的计算公式为：

为证明复杂度计算公式的有效性，取大小一样两幅图像进行复杂度计算（排除图像大小对结果的影响），利用本文的复杂度计算公式，计算比较图2中（a）和（b）两幅图像的复杂度。

图2 实验图像Fig.2 The experimental image

两幅图像的灰度直方图如图3所示。

从两幅图的灰度直方图的灰度分布情况可以看出，两幅图像具有相似的直方图分布。所以采用灰度直方图不能很好地对两幅图像进行区分，也表明灰度直方图并不能反映图像中灰度的空间分布情况。图像复杂度统计见表1。

图3 灰度直方图Fig.3 Gray histogram

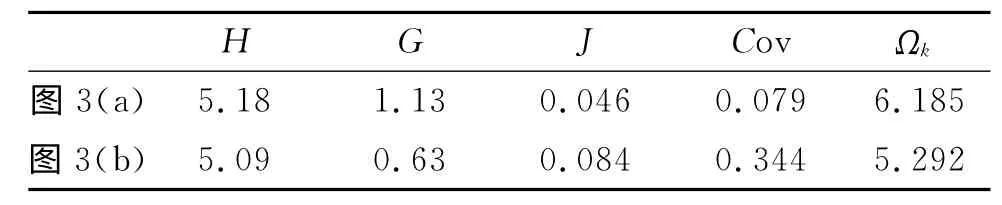
表1 图像复杂度统计简表Tab.1 Statistical table of the test image complexity

比较从表1得到的实验结果，图3（a）的复杂度明显高于图3（b）计算得到的复杂度。实验结果与人裸眼目测结果一致，说明本文提出的复杂度计算公式能够客观真实地反映出图像的复杂度，能全面地描述图像中灰度值和灰度值的空间分布情况。但对于以信息熵为基础的改进图像描述方法，两幅图像的信息熵H 差异很小，很难完成对于两幅图像的区分。所以从对图像描述的全面性上看，本文提出的图像复杂度计算方法优于传统的灰度直方图和以信息熵为基础的描述方法。

2 基于图像复杂度的阈值分割算法

应用阈值法进行的图像分割，是以图像中灰度的突变为基础进行的。实际图像分割过程中，灰度的突变模型分为三类：1）台阶模型；2）斜坡模型；3）屋顶边缘模型［13］。无论哪种边缘模型，从灰度的空间分布可以看出，待分割边缘具有丰富的灰度级分布，且灰度的空间排列往往是随机的杂论无章的。

基于前文的复杂度计算公式中出现的各个度量参数和参数对图像复杂度计算结果的影响程度可以判断，待分割图像边缘点所在邻域具有较大的复杂度，高于图像背景区域各点邻域的复杂度。孤立的噪声点尽管会引起局部梯度的突变，但对复杂度的影响较小（复杂度表征的是灰度级别的不同，与灰度幅值无关），因此复杂度本身具有一定的滤波作用［14］。所以可以用图像复杂度的这些优点以及它和待分割边缘点之间的联系，进行图像分割。

2.1 算法思想

利用图像复杂度计算公式计算出整个图像的整体复杂度。根据图像的整体复杂度选取合适大小的邻域尺寸窗作为移动窗口。从图像左上角开始，分别计算各个像素邻域尺寸框内的图像复杂度，并把计算得到的局部复杂度赋值给相应像素。由此可以得到经复杂度计算变换后的复杂度图像。在变换后的复杂度图像中，原图像中的边缘点，因为其同质性差，灰度层次丰富，将具有较大的复杂度值。原图像中的背景区域，由于具有较好的同质性和相对单一的灰度空间分布复杂度得到进一步降低。这样原图像的待分割区域和背景区域的区别的到了加强，而且由于局部复杂度具有良好的滤波降噪效果。所以只要选取合适的复杂度值，就可以很好的把目标和背景分割开来，达到良好的分割效果。

2.2 算法设计步骤

基于上述的算法思想，本文所阐述算法的流程图如图4所示。

1）利用图像复杂度计算公式（6）计算整幅图像的整体复杂度Ωk。

2）根据整体复杂度值设定邻域窗尺寸，邻域窗口尺寸一般使用固定的尺寸，且一般取正方形M×M ，M 表示所含像素个数。

3）利用图像复杂度计算公式（6）分别计算图像各个邻域的局部复杂度Ωij，并把复杂度的计算值赋值给中心像素，得到新的变换后的复杂度图像。

4）利用最大类间方差法，计算出复杂度阈值T。

5）根据阈值法基本原理进行图像分割分别记录边缘点的坐标位置。

6）根据记录的坐标点位置，在原图像中提取出边缘点，完成图像的分割。

邻域窗口大小的选择应以图像整体的复杂度作为基准，对于复杂度较大的图像，应选取尺寸较小的邻域窗口，这样能保证不遗漏原图像中的信息，相反若图像整体复杂度较小，则应选取尺寸较大的邻域窗口较大的邻域窗口，在保证分割效果的基础上，提高算法的效率。

图4 算法流程图Fig.4 Algorithm flow chart

3 实验验证

为验证本文提出算法的有效性，以及在实际应用中的效果。本文采用图2（a）、（b）两幅图像作为实验验证对象，并与经典的Ostu阈值分割方法和以信息熵为基础改进图像分割方法进行效果对比。

运用Ostu阈值分割法对图像进行阈值分割，得到图5（a）、（b）两幅分割结果。通过观察发现Ostu法并没有得到良好的分割结果，待分割区域没有全部从图像中分割出来，存在明显的欠分割现象。图像分割结果的有效性、完整性并没有得到保证。通过细致分观察图5的（a）、（b）两幅图像，发现未被分割的部分具有明显的特征，它们都与图像的背景具有相似的灰度值，在灰度直方图中处于相近的位置。所以单纯以灰度直方图为依据对阈值进行选取，并不能把这两部分进行很好的区分，分割结果的完整性、有效性也得不到应有的保证。

采用改进的以信息熵为基础的图像分割算法，得到图5（c）、（d）两幅分割结果。通过与图5（a）、（b）比较发现，分割结果并没有得到显著的改善。信息熵虽然能反映图像中所包含内容的多少，较灰度直方图有所改进，但依然无法描述图像中各灰度级的空间分布信息，是一种有待改进的图像描述方法。

图5 图像分割结果Fig.5 The results of image segmentation

利用本文提出的新算法对图像进行分割，得到图5中（e）、（f）两幅图像。通过与图5中（a）、（b）、（c）、（d）四幅图像进行比较发现，新算法对图像进行了准确、完整地分割，与背景区域具有相似灰度值的待分割区域也被完整准确地分割出来，分割结果较之前有了明显的改善。从理论分析角度，不难发现：尽管待分割部分与背景具有相似的灰度值，但同时待分割边缘也具有了丰富的灰度级分布即具有高于其他部分的图像复杂度。所以从图像复杂度角度出发很容易对于所需阈值进行选取，并完成对背景和目标区域边界的准确区分。

通过实验对比，发现基于复杂度的图像分割算法不仅是可行的、有效的，还在保证图像分割结果有效性、完整性方面远远优于传统的阈值分割方法和信息熵为基础的改进图像描述方法。

4 结论

本文以综合反映图像灰度级空间分布的图像复杂度为标准，提出了基于图像复杂度的分割算法。该算法以能完整描述图像中灰度空间分布的图像复杂度为基础，具有一定的滤波降噪作用，保证了以它为依据进行阈值选取的准确性和有效性。

实验结果表明，该算法优于经典的阈值分割算法和以信息熵为基础的改进图像分割算法，且在图像分割的完整性和有效性方面表现出了良好的分割性能，是一种有效的新算法。

［1］Rafael C Gonzales，Richard E Wood.Digital Image Processing［M］.北京：电子工业出版社，2011.

［2］Kapur J，Sahop P，Wong A.A New Method for Grey-Level Picture Thresholding Using the Entropy of the Histogram［J］.Computer Vision Graphics and Image Processing，1985，29：210-239.

［3］Abutaleb A S.Automatic Thresholding of Gray-Level Picture Using Two-Dimensional Entropies［J］.Pattern Recognition，1989，47：22-32.

［4］李欣，赵亦工，郭伟.基于复杂度的自适应门限弱小目标检测方法［J］.光子学报，2009，38（8）：2144-2149.

［5］赵峙江，赵春晖，张志宏.一种新的PCNN 模型参数估算方法［J］.电子学报，2007，35（5）：996-1000.

［6］高振宇，杨晓梅，龚剑明，等.图像复杂度描述方法研究［J］.中国图像图形学报，2010，15（1）：129-135.

［7］钱思进，张恒，何德全.基于图像视觉复杂度计算的分类信息隐藏图像库［J］.解放军理工大学学报（自然科学版），2010，11（1）：26-30.

［8］吴一全，张金矿.二维直方图θ划分最大Shannon熵图像阈值分割［J］.物理学报，2010，59（8）：5487-5494.

［9］高士忠.基于灰度共生矩阵的织物纹理分析［J］.计算机工程与设计，2008，29（16）：4385-4388.

［10］宁顺刚，白万民，喻钧.基于灰度共生矩阵的图像分割方法研究［J］.电子科技，2009，22（11）：69-71.

［11］桑庆兵，李朝锋，吴小俊.基于灰度共生矩阵的无参考模糊图像质量评价方法［J］.模式识别与人工智能，2013，26（5）：492-497.

［12］郑红，李钊，李俊.灰度共生矩阵的快速实现和优化方法研究［J］.仪器仪表学报，2012，33（11）：2509-2515.

［13］刘松涛，殷福亮.基于图像的分割方法及其新进展［J］.自动化学报，2012，38（6）：911-922.

［14］闫成新，桑农，张天序，等.基于局部复杂度的图像过渡区提取与分割［J］.红外与毫米波学报，2005，24（4）：312-316.