基于总体最小二乘的多基地声纳系统定位算法
李 涛,屈也频,梅风华
(海军装备研究院航空装备论证研究所,上海 200436)
0 引言
多基地声呐定位技术由于其在覆盖范围、定位精度、抗隐身能力和战术使用上的优势,已成为现阶段声呐技术领域研究的热点[1-2]。现有的多基地声呐系统通过获得目标的方位角、距离和多普勒频移等测量结果,结合目标与多基地声纳的相对位置关系解算出目标坐标[3-7],但这种算法受测量误差影响,在某些区域定位性能非常差。在多基地情形下,利用不同接收站的测量信息存在数据冗余的特点,充分利用各个接收站所获得的测量数据可以改善这种现象[8],文献[9]和[10]则从提高测量信息利用率的角度,分别研究了基于卡尔曼滤波的单枚、多枚被动定向浮标定位算法,但共同的缺点是需已知测量信息的误差模型。针对常规解算法进行多基地声纳系统定位时,定位精度和稳健性受测量误差影响严重的问题,提出基于总体最小二乘法的多基地声呐定位算法。
1 多基地定位原理
以T-R3型多基地声呐系统为例,考虑到声纳作用距离通常要高出探测目标深度一个数量级以上,即目标的垂直向的俯仰角很小,故只在水平坐标内考虑定位,以发射站为原点建立二维直角坐标系,各基站的几何关系如图1所示。
根据图1所示的几何关系,可得目标的定位方程如式(1)。
式(1)中,ρi=vτi,为发射站与第i个接收站之间的传播距离,v为水中声速,τi为发射站与接收基站之间的传播延时,通过收发基地时间同步后,可以实现时延的测量。易知具有相同ρi 的目标的轨迹集合构成等时到达椭圆;θi由浮标定向测出,具有相同θi的目标轨迹集合构成过接收站点的直线。易知式(1)方程组存在双解,为消除模糊性,实际情况下可以通过附加浮标作用距离信息、多址数据融合以及目标轨迹连续等方法予以消除。

图1 多基地声纳系统定位原理Fig.1 Position principle of multistatic sonar
由于ρi、θi及xi、yi均存在测量误差,式(1)的解算结果会出现误差,甚至无解,这在目标靠近发射站与接收站连线(基线)时会更加突出,这是由于此时式(1)的第一个方程由于测距误差的存在而不成立所致。当存在多个接收站同时检测到目标时,可通过信息综合处理技术提高定位精度,最简单的情况是对各个接收站的解算结果取平均

式(2)中,x(j)、y(j)为第i个有效接收站方程的解,xd、yd为综合后的解算结果,p 为存在有效解的接收站数目。
2 基于总体最小二乘的定位算法
式(1)、式(2)的定位算法受ρi、θi及xi、yi的测量误差影响较大,在多个接收站同时检测到目标的情形下,由于存在冗余探测信息,为了综合利用不同接收站的测量信息,引入总体最小二乘方法来解决目标定位问题,其实现原理为:将测量方程进行一定的数学变换,消去二次项,得到一组新的线性方程组。线性方程组的总体最小二乘解就是目标的位置估计。
将式(1)消去二次项得

利用两个接收站的测量结果消去未知量τT、τi,可得

因此,利用多个接收站的测量结果可以建立线性方程组

其中An×2、Bn×2为n×2维矩阵,dn、hn为n 维向量,n为接收站数目,且
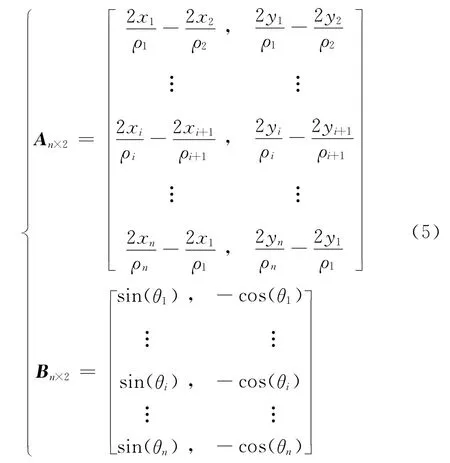

式(4)实际上是一组超定方程,通常可以通过最小二乘法来求解。观察式(5)和式(6),由于ρi、θi及xi、yi均存在测量误差,导致An×2、Bn×2及dn、hn均存在误差,由于最小二乘法求解的过程只考虑将dn及hn的误差最小化,不适合An×2、Bn×2均存在误差的情形,因此下面基于总体最小二乘算法来求解式(4)。
将式(4)改写为:
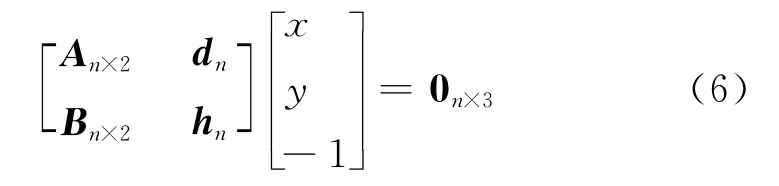
令

总体最小二乘法的求解过程即考虑误差矩阵En×3,使得解,取最小特征值对应的特征向量u,则
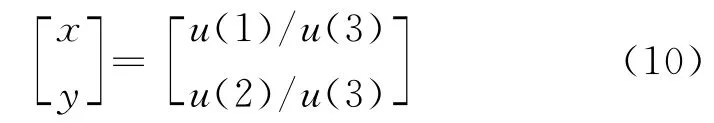
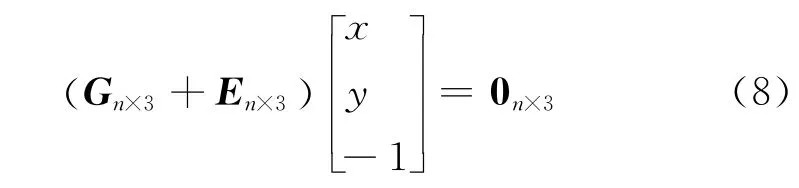
1)确定初始值u0、a,其中u0为任意3维向量

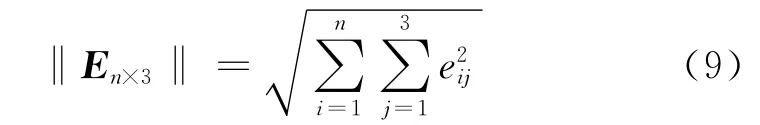
可见总体最小二乘法考虑的是将An×2、Bn×2及dn、hn的总体误差最小化,因而更适 合式(4)的求解。
求解总体最小二乘解需对GTn×3Gn×3进行特征分
3 计算机仿真
仿真试验通过式(1)、式(2)的直接解算法和基于幂迭代的总体最小二乘法来比较验证。
试验1 设接收站个数为3,接收站坐标(5.4km,-8.4 km)、(10 km,0)、(5.4 km,8.4km),目标坐标为(5km,2km),浮标散布范围分别服从100 m、1 000 m 和2 000 m 内的均匀分布,测向和测距误差服从正态分布,对不同测向和测距方差下的定位方差进行1 000次蒙特卡罗仿真,图2给出了仿真的结果。
图2的结果显示,直接解算法在测距误差及浮标散布范围增大时定位误差迅速增大,显示其对测距误差和浮标散布范围非常敏感。采用总体最小二乘法较之直接解算法具有更好的定位精度,且稳定性远高于直接解算法,尤其是在测距误差及浮标散布范围较大时,总体最小二乘法显示出抑制误差的优异性能。
试验2 设接收站个数为3,接收站坐标(5.4km,-8.4 km)、(10 km,0)、(5.4 km,8.4km),改变目标坐标为(9.5km,0.5km),此时,目标更加接近发射站与接收站连线。设浮标散布范围分别服从100m、1 000m 和2 000m 内的均匀分布,测向和测距误差服从正态分布,对不同测向和测距方差下的定位方差进行1 000次蒙特卡罗仿真,图3给出了仿真的结果。

图2 给定浮标散布范围时不同测向和测距误差下的定位方差Fig.2 Positionvariance for different direction and distancemeasure error when specify buoy spread area

图3 给定浮标散布范围时不同测向和测距误差下的定位方差(目标靠近基线)Fig.3 Positionvariance for different direction and distance measure error when specify buoy spread area(target near baseline)
图3显示结果与实验1相似,总体最小二乘法较之直接解算法具有更好的精确性和稳定性。同时,由于目标处在基线附近,采用式(1)解算时,会出现无解的情形,且出现无解情形的频数随测距误差的增大而增大,但采用总体最小二乘法时,由于其能很好的拟合测量数据,即使是目标处在基线附近且测距误差较大的情形,依然能够取得很好的定位精度,具有更好的稳健性。
4 结论
本文提出了基于总体最小二乘法的多基地声纳系统定位算法,该算法首先将测量方程进行一定的数学变换,得到一组新的线性方程组。通过求解线性方程组的总体最小二乘解估计目标位置。仿真表明较之常规的解算法能够取得更好的定位精度和稳定性,同时解决了目标处在基线附近,常规解算法随测距误差的增大而会出现无解情形的问题。
[1]Coraluppi S.Multistatic sonar localization[J].IEEE Journal of Oceanic Engineering,2006,31(4):964-974.
[2]Sergey S.Localization in airborne multistatic sonars[J].IEEE Journal of Oceanic Engineering,2008,33(3):278-288.
[3]胡柱喜,孙明太,苏维国.被动定向浮标LOFIX 定位精度分析[J].电光与控制,2009,16(12):26-29
[4]孔银垒,王英民.DIFAR 浮标反正切目标方位估计方法[J].声学技术,2010,29(4):370-373
[5]王隽,王英民,陶林伟.浮标定位算法的仿真研究[J].声学技术,2009,28(6):95-98
[6]杨蕾.被动型声纳浮标定位技术研究[D].哈尔滨:哈尔滨工程大学,2009.
[7]白菊蓉,毛永毅,张宝军.多基地雷达空间定位算法和精度比较[J].西安邮电学院学报,2008,13(1):18-21.
[8]侯志国,何强,罗晓松.声探测多传感器多目标定位与跟踪方法[J].电声技术,2010,34(9):40-42.
[9]陶林伟,王英民.一种新的单枚被动定向浮标目标定位方法[J].兵工学报,2011,32(3):365-369
[10]陶林伟,王英民.基于扩展卡尔曼滤波的DIFAR 浮标阵定位算法及分析[J].西北工业大学学报,2009(5):738-744

