异形斜交简支T梁桥受力性能分析

王 彬

（山西省交通科学研究院，山西 太原 030006）

异形斜梁桥顾名思义就是两端桥跨支撑端，一端正交，一端与路线前进方向斜交的桥型。相对异形斜梁桥还有正交梁桥和斜交梁桥，正交梁桥是两个支撑端都是正交的，斜交梁桥是两个支撑端都与路线前进方向斜交。异形斜梁桥无论在高速公路还是市政道路上都得到了迅速的发展，这是因为其不但能改善道路线形及适应城市立交的要求使路线线形更加流畅，而且可以缩短线路和桥跨，从而节省道路用地、工程造价和投资，提高经济效益。但由于斜交角度、桥面宽度等因素的影响使异形斜交T梁的受力分析比正交简支T梁复杂得多，因此本文以实际工程为研究对象，分析在桥面宽度及斜交角度一定的条件下异形简支T梁的受力状态[1-3]。

1 工程概况

某高速公路大桥为跨越铁路及河流而设，桥跨与铁路线交角60°，路基宽度26 m。该桥单幅上部结构为5×30 m装配式预应力混凝土简支T梁，单片T梁梁高2.5 m，单幅横向布置5片，在跨中、1/4处设置横隔板，两支撑端沿横向支撑线各设置一道端横隔板。由于该桥第2孔跨越铁路为斜交桥，两端斜交角度均为30°。主桥第1跨为异形简支T梁桥，一端正交，另一端斜交角度为30°，1号内边梁跨径32.927 m，5号外边梁跨径27.073 m，两者相差5.854 m，中间3号中梁跨径为标准跨径30 m，T梁结构布置形式如图1～图2所示。简支T梁按部分预应力混凝土A类截面控制设计；该桥位处无不良地质；下部结构采用柱式墩、柱式台、钻孔灌注桩基础。该桥的技术指标为：

a）设计荷载 公路-I级；

b）桥面净宽 2×11.5 m；

c）地震动峰值加速度 0.05g；

d）设计洪水频率 1/100。

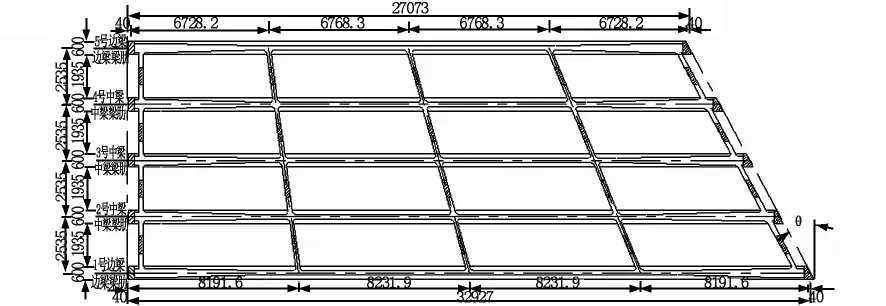
图1 异形简支T梁桥平面布置图（单位：mm）

图2 异形简支T梁桥横向布置及构造图（单位：mm）

2 研究分析方法

目前，比较常用的计算方法主要是将简支T梁桥空间分析近似地分解为纵桥向和横桥向分别进行计算，但由于分析3种桥型状态，按照单梁分析显然是不合适的，为了更好地模拟简支T梁的空间受力状态，本文采用梁格法建立模型，即将分散在梁的每一区段的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内，按照结构刚度等效的原则，采用MIDAS CIVIL建立分空间分析模型。两端均正交的正交梁格模型如图3所示；两端斜交角度均为30°的斜交桥梁格模型如图4所示；一端正交，一端斜交角度为30°的异形斜梁桥梁格模型如图5所示，标准跨径均为30 m[4]。

为研究分析异形斜交简支T梁的受力性能，本文按照该实际工程的桥型布置，分别分析正交、斜交、异形斜交简支T梁在相同条件下几种荷载工况作用影响的受力性能，并分析引起差别的原因。

图3 正交梁格模型

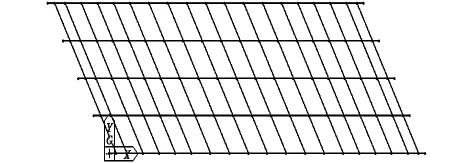
图4 斜交梁格模型

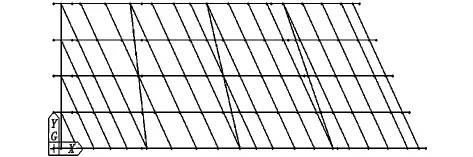
图5 异形梁格模型

3 结构受力性能分析

3.1 自重荷载作用主梁受力分析

分别计算3种梁格模型，在自身重量作用下，成桥状态时主梁内力分析数据如表1所示。

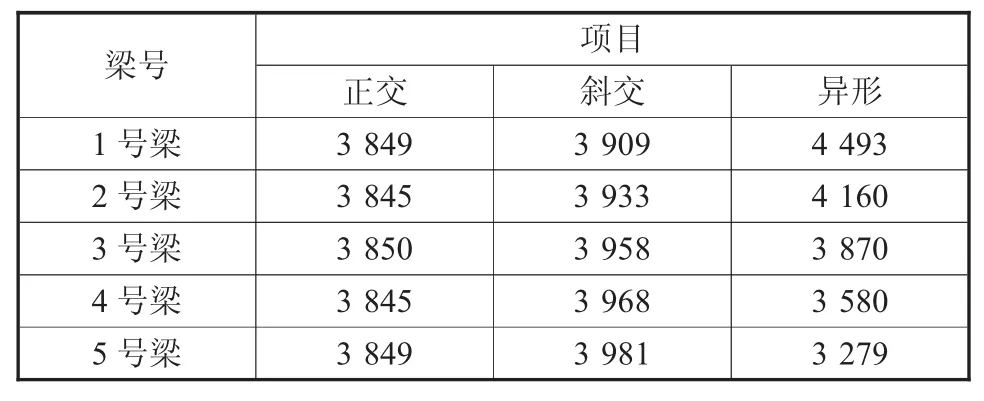
表1 跨中正弯矩 kN·m

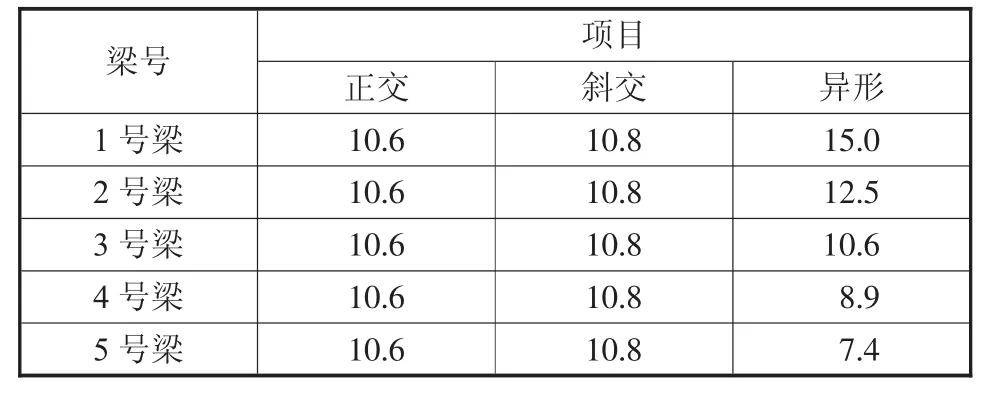
表2 跨中挠度 mm

从表1可以看出异形梁跨中最大弯矩从1号梁到5号箱式逐渐减少的，而正交梁及斜交梁变化不大，这是由于在自身恒载作用下，正交梁及斜交梁单片梁长度是一样的，异形梁由于每片梁的长度不同，1号梁比5号梁大了近37%，这是由于每片梁每延米的重量相当，而随着跨径的增大，本身重量也在增大，跨中正弯矩较大。表2反应的是在自重作用下，正交及斜交梁单片梁的挠度基本一样，而异形梁1号梁比5号梁大了近103%，这是由于每片梁长度不同造成每片梁的线刚度不同，在荷载作用下，每片梁的跨中最大挠度值也不同。

3.2 二期铺装荷载作用下主梁受力分析

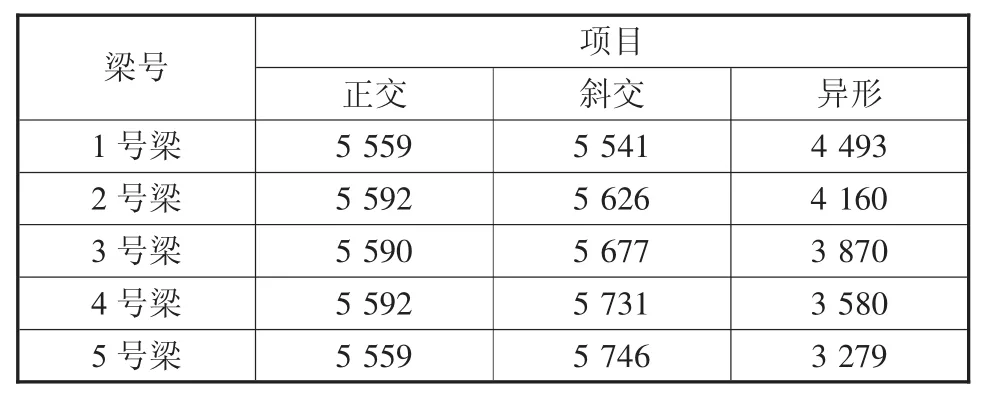
表3 跨中正弯矩 kN·m

从表3可以看出在铺完桥面铺装以后，正交梁的1号梁和5号梁、2～4号梁的跨中弯矩基本一样；斜交梁1号梁与5号梁跨中弯矩小5%左右，2～3号梁逐渐增大，这是由于斜交梁扭矩的影响加大，使得跨中正弯矩分布不均；弯扭耦合作用在异形梁上作用更明显，由于每片梁的长度不同，1～5号梁每片梁的弯矩大小不同。

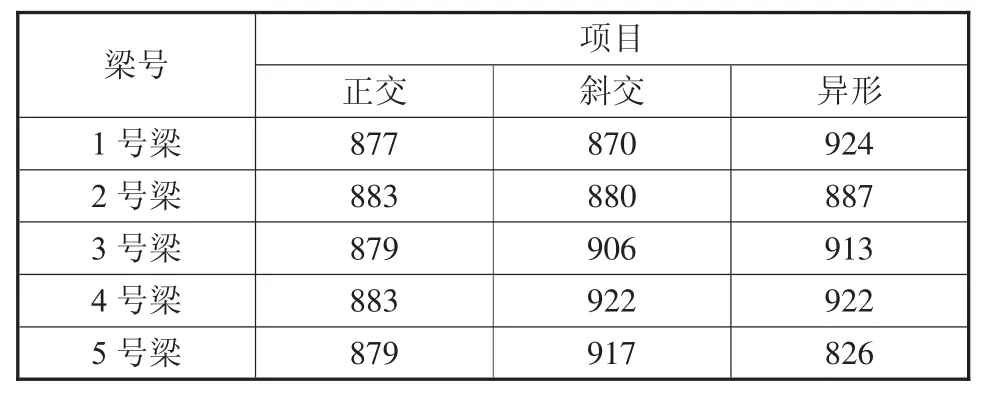
表4 支座反力 kN

从表4可以看出正交梁的支座反力分布与跨中正弯矩分布趋势基本一致；斜交梁支座分布趋势是1号梁到5号梁是逐渐增加的，也就是说由于横向连接刚度的影响，主梁支座从锐角区到钝角区时逐渐增大；对于异形梁由于横向连接刚度和各主梁长度不一造成支座反力分布极不均匀，差异较大，但总体变化趋势与斜交梁一致[5]。

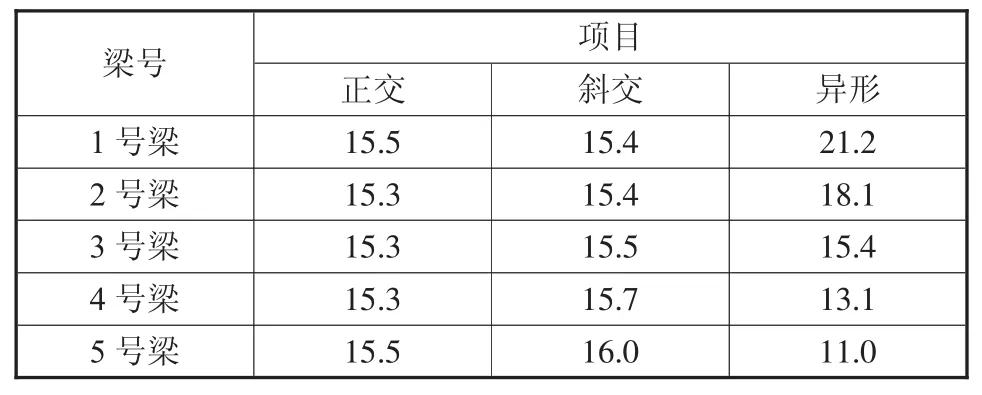
表5 跨中挠度 mm

从表5可以看出正交梁在二期铺装完成后，各片主梁的跨中挠度基本相同；斜交梁跨中挠度的变化基本与支座反力变化趋势相同，即从锐角区到钝角区时逐渐增大；对于异形梁，由于各片主梁长度不一，1号主梁大于标准跨径30 m，所以1号主梁跨中挠度最大，5号主梁长度最小跨中挠度最小，其变化趋势也由于横向连接刚度和各主梁长度不一而影响其挠度大小[6]。

3.3 活载作用下主梁受力分析

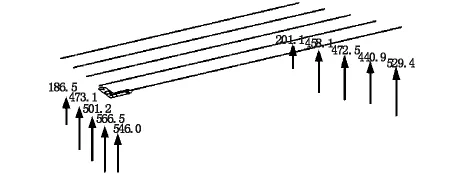
图6 活载偏1号边梁方向支座反力（单位：kN）

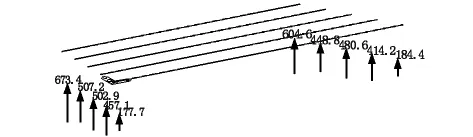
图7 活载偏5号边梁方向支座反力（单位：kN）

图8 活载偏1号边梁方向挠度等值线图（单位：mm）

图9 活载偏5号边梁方向挠度等值线图（单位：mm）

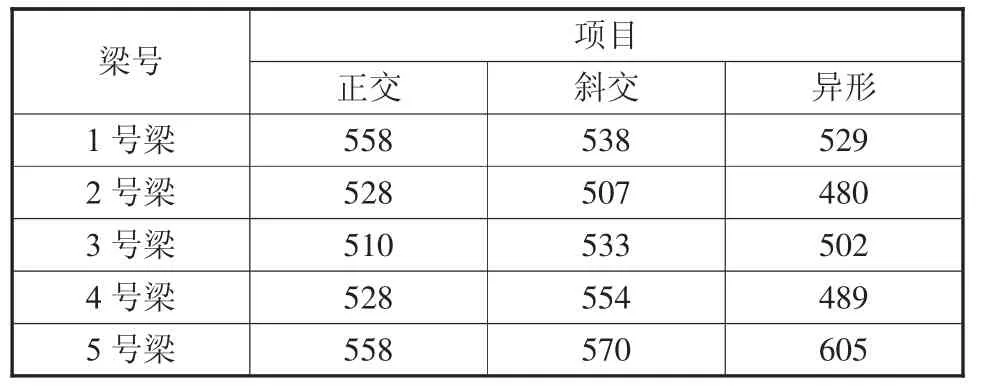
梁号 项目正交 斜交 异形1号梁 558 538 529 2号梁 528 507 480 3号梁 510 533 502 4号梁 528 554 489 5号梁 558 570 605

梁号 项目正交 斜交 异形1号梁 6.8 6.5 8.1 2号梁 5.4 5.3 6.4 3号梁 4.9 4.9 5.2 4号梁 5.5 5.7 4.9 5号梁 6.8 7.1 5.5

从表6及图6～图7可以看出在按最不利布载方式下正交梁的边梁支座反力最大，3号中梁支座反力最小；斜交桥由于横向连接刚度的影响使弯扭耦合，耦合作用较突出，使支座反力除了正交梁的分布外，还有从锐角区到钝角区时逐渐增大的趋势；异形梁5号最短长度边梁的支座反力最大，而1号边梁的支座反力比5号小近15%，这是由于横向连接刚度和各主梁长度不一的双重影响造成的，由此可见当异形梁角斜交角度足够大，汽车布载最不利时，可以使锐角区域的主梁在活载作用下支座呈现拉力，这在以后的实际中要重视。

从表7及图8～图9可以看出在按最不利布载方式下正交梁及斜交梁的变化趋势与支座反力是相通的，而异形梁由于每片梁的线刚度不同，其变化趋势与上述两种桥型不同，由于1号梁的线刚度最小，其在靠近1号梁最不利布载时，产生的跨中最大挠度是最大的，但5号边梁由于其线刚度最大，但在靠近5号边梁布载时跨中仍产生了不小的竖向挠度，同理可以分析中梁的跨中挠度值。

4 结论

a）异形斜梁桥在自重作用下，由于单片梁的长度不一，造成跨中正弯矩、挠度值与正交梁及斜交梁不同，但3号梁基本相当。

b）由于横向连接刚度和各主梁线刚度不同造成异形斜梁桥在二期恒载跨中正弯矩、挠度值较正交梁及斜交梁不同，差异较大，但总体变化趋势与斜交梁一致。

c）异形斜梁桥在二期恒载作用下支座反力从锐角区到钝角区时逐渐增大，这与斜梁桥支座反力变化趋势是一致的。

d）异形梁由于弯扭耦合作用比较突出，在活载作用下主梁支座反力及库中最大挠度分布是极不均匀的。