基于振动能量收集的传感器自供能技术研究
宋 宇, 宋隽炜
(长春工业大学 计算机科学与工程学院,吉林 长春 130012)
基于振动能量收集的传感器自供能技术研究
宋 宇, 宋隽炜
(长春工业大学 计算机科学与工程学院,吉林 长春 130012)
复合式能量收集技术是一种基于压电和电磁的传感器自供电技术。对复合式能量收集系统进行分析,给出系统的数学模型,讨论系统共振频率与系统结构参数的关系;设计了一种压电和电磁复合式能量收集装置,并进行实验验证。结果表明:给出的数学模型基本反映了系统的输出特性,在共振频率为18 Hz时,与单一型电磁技术实验在共振频率处得到的3.2 mW负载功率相比,复合式能量收集技术获得的最大负载功率3.8 mW,增加了19 %。
环境振动; 能量收集; 压电能量转换; 电磁能量转换; 无线传感器
0 引 言
随着大规模高集成度电路的广泛应用,微电子系统的物理尺寸变得越来越小,系统功耗也得到了明显的降低,使得低功耗器件的研究越来越热,这些器件的驱动能源通常是电池。但伴随着器件数量的急剧增加和物理尺寸的减小,电池的更换随之增加,甚至在某些条件下,无法完成电池的更换工作。工作在用电设备上面的传感器由大容量的电池和大容量电容器进行供电,这样不仅使得对电子设备很难进行很好的维护,而且也造成了环境污染[1]。因此,亟需一种可行的通过收集和转换周围环境振动能量而实现对低功耗器件供能的方法[2~3]。振动能量收集技术是目前正在研究的一种热门方式,这种供电方式可以延长低功耗设备的寿命,并可以不依赖电池或者线束对设备进行单独供电[4]。
单一的供电方式并不足以满足电子产品的电力需求[5]。由于压电材料的可用性强、性能好、可以提供更高的输出电压等优点[6],人们广泛关注利用压电效应的能量收集技术。此外,由于电磁式能量收集具有设计方便、制作简单而且易于分析的特点[7],使得电磁能量收集技术也得到进一步发展。
很多文献对使用不同的能量收集方法来提高振动能量收集的效率进行了报道[8,9]。Jiang S等人从改善能源效率的角度对压电双晶片的悬臂梁发起了一项研究[10],通过在压电悬臂梁的末端添加小质量块的方法来提高能量收集器的效率。中东技术大学研究人员致力于电磁微发电的原理研究和应用于生产的能量收集器[11]。先前的压电振动能量收集研究大多集中在开发新产品和改进压电材料系统的能源收集效率,或集中研究在共振频率状态下可以调整收集结构,以满足环境振动的要求[12]。
本文研究电磁与压电复合式振动能量收集的方式,对其进行建模,并对模型进行仿真研究,设计搭建了电磁与压电振动能量回收装置。实验结果表明:与单独压电或电磁能量收集结构相比较,复合结构能够输出更多的能量。在共振频率为18 Hz时,复合式能量收集装置的最大负载功率为3.8 mW,相比于采用单一的电磁技术时的最大负载功率3.2 mW增加了19 %,能满足间断、脉冲式模式工作的负载,例如:无线传感器网络中的故障监测元件。
1 复合能量收集系统建模
1.1 系统结构与原理
基于振动的复合能量收集装置用如图1所示。该装置是由末端带有质量块的压电悬臂梁和一组线圈组成。永磁质量块用来激发振动和调整共振频率,同时为其下放置的线圈提供了变化的磁场。悬梁臂的振动由外部振动引起。永磁铁与线圈相对运动在闭合的线圈中实现了电磁能量转换,与此同时,压电片受到应力的作用产生电荷,整合这两部分能量使得输出的总能量增加。

图1 压电与电磁综合发电装置示意图
1.2 复合式振动能量收集系统模型
电磁—压电混合式振动能量收集装置运动学的模型[2]描述为
(1)

2 复合式振动能量收集系统共振频率分析与仿真
2.1 压电悬臂梁共振频率的分析
为使输出频率达到最大,首要的是装置的共振频率必须与环境振动频率相一致,当振动频率与共振频率之间存在微小偏差时输出功率减小。通常,共振频率的计算公式为
(2)
式中 fr为共振频率;ω为角频率;K为悬臂梁的弹簧常数;me为悬臂梁的有效质量。当小质量块远小于悬臂梁的长度时,将小型质量块当做一个点质量来计算,这种简化方法在某种程度上可以很有效地来进行计算。为计算没有质量块的悬臂梁的共振频率,现在有两种方法可供选择。
按照折弯刚度EI可以用来计算没有质量块的悬臂梁的共振频率
(3)
或者弯曲模量(E0=EI/w)来计算没有质量块的悬臂梁的共振频率
(4)
式中 fn为谐振频率;νn为特征值;l为悬臂梁的长度;E为弹性模量;I为中性轴的惯性矩;m为悬臂梁的单位长度质量;w为悬臂梁的宽度。对于双晶压电片这种复合材料,E0为两种材料的杨氏模量计算函数,EP(压电陶瓷)和ES(黄铜)及其厚度tp和ts满足如下关系
(5)
每一单位面积质量m通过厚度和密度来计算,ρp和ρs为两种材料的密度
m=2ρptp+ρsts.
(6)
在自由端有一个小型质量块的悬臂梁的共振频率可以通过以下公式近似估计
(7)

(8)
然而,当这个小型质量块是分布在一个区域内而不是通过一个点来表示,它可以用质量块的中心为轴,以一个集中的点来看待。对于一个均匀密度的矩形分散的小质量块,对称轴位于自由端,重心位于远离lm/2的位置。悬臂梁在这个位置的有效弹簧常数K′和有效弹簧常数K有关
(9)
用K′取代方程式(8)中的K,自由端带有小质量块的悬臂梁的复合双晶压电片的共振频率表示为[4]
(10)
Δm=ρmlmwmhm,
(11)
式中 ρm,lm,wm和hm分别为质量块的密度、长度、宽度、高度。
使用上面的方程可以计算悬臂梁的共振频率参数,通过改变悬臂梁上的小质量块的长度和宽度可以来改变共振频率。
2.2 压电振动能量复合收集系统仿真
利用Matlab软件对压电振动能量复合收集系统模型进行了数值仿真,压电悬臂梁共振频率与悬臂梁的长度、悬臂梁的宽度、质量块的长度、质量块的高度以及压电陶瓷片的结构参数的关系如图2所示。

图2 共振频率与悬臂梁结构参数的关系
从图2可以证实,共振频率随着压电陶瓷片的长度和小质量块尺寸的增加而降低,随着压电陶瓷和金属垫片的厚度的增加而增加,随着悬臂梁的宽度的增加而升高,但随着小质量块的增大其保持不变。
3 压电振动能量复合收集系统性能测试与分析
3.1 压电振动能量复合收集系统设计与实验
由仿真分析可以看出:收集装置的共振频率与悬梁臂的结构参数相关联。通过改变压电片和基片板的长度、宽度、厚度等参数,可以调节系统的共振频率。系统共振频率设计为18Hz,结合仿真分析,最终确定了压电悬臂梁结构尺寸参数,如表1所示。
表1 复合式能量收集装置的参数
Tab 1 Parameters of composite energy collecting device
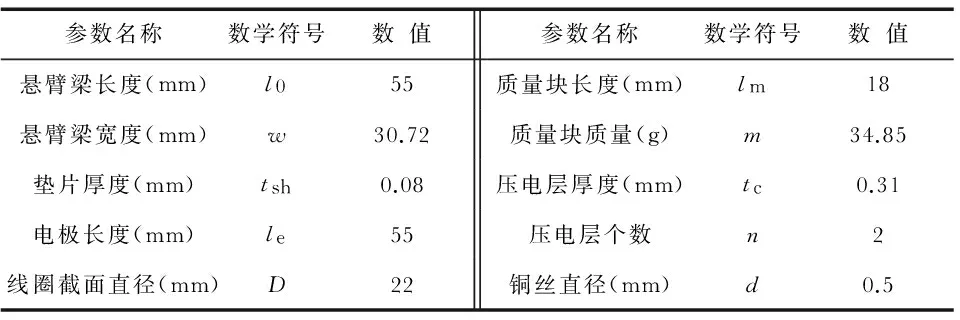
参数名称数学符号数值参数名称数学符号数值悬臂梁长度(mm)l055质量块长度(mm)lm18悬臂梁宽度(mm)w30.72质量块质量(g)m34.85垫片厚度(mm)tsh0.08压电层厚度(mm)tc0.31电极长度(mm)le55压电层个数n2线圈截面直径(mm)D22铜丝直径(mm)d0.5
3.1.1 实验原理
计算机编程输出正弦波送给SD1492功率放大器,功率放大以后送给SD1482激振器,通过它来模拟实际振动。此时,复合能量收集装置开始工作,压电和电磁的输出给能量转换与存储电路对负载进行供电,数据采集卡采集相关的数据供分析。实验原理如图3。

图3 实验原理
3.1.2 能量收集存储电路设计
图4所示的电路的基本原理是:压电电磁发电机产生的电能经过整流桥,将电能存储在超级电容器中,再经过实用的调压芯片直接供给负载。采用型号为DF005S的整流桥,调压芯片采用TI公司的TPS62200。
本文采用了两个能量收集存储电路,一个用于采集压电的能量,一个用于采集电磁的能量,经过调压芯片分别处理后再存储在一个超级电容器中。

图4 能量收集存储电路框图
3.2 实验结果分析
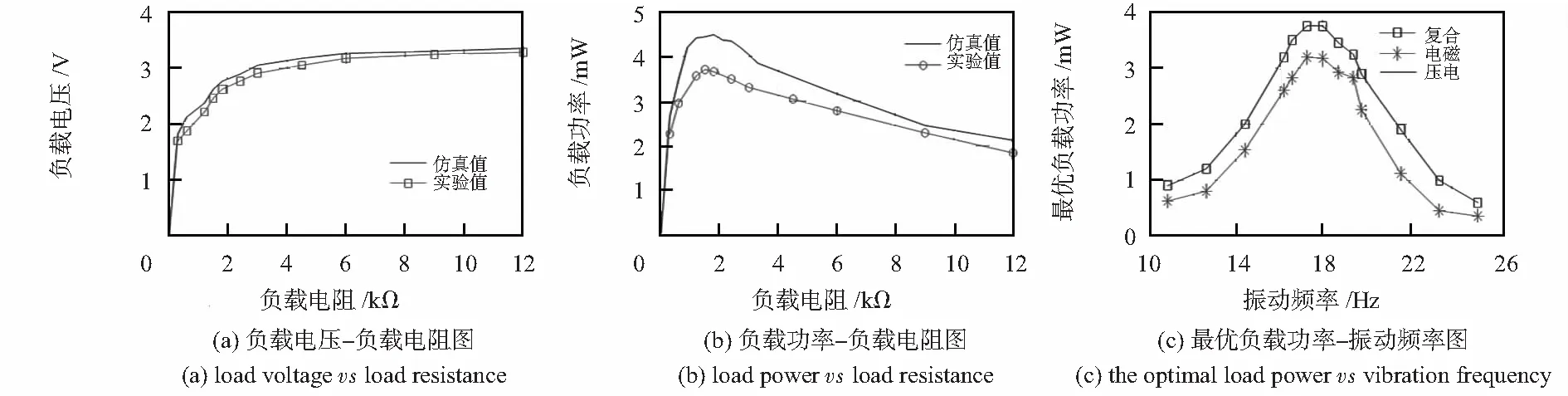
图5 仿真与实验结果对比
复合式能量收集装置的最优负载电阻是由内部等效电路和转换电路的参数决定的,利用PSPICE仿真和实验方法确定最优负载电阻值约为1.5 kΩ。从图5(a)中看出:负载电压始终随着负载电阻的增大而上升。从图5(b)可以看出:负载功率首先呈上升趋势并在最佳负载电阻时达到峰值,当负载电阻大于1.5 kΩ时负载功率随之下降。在最优负载电阻时的运用数值仿真计算负载电压与负载功率分别为2.6 V与4.48 mW,测量值则为2.4 V与3.8 mW,测量值与仿真值很接近。
图5(c)显示了最优负载电阻时复合式和单一能量收集技术的最优负载功率,与单一型电磁技术实验在共振频率处得到的3.2 mW负载功率相比,复合式能量收集技术获得的最大负载功率3.8 mW,增加了19 %。单一压电工作模式下的最优负载功率较低,其稳定后值为0.75 mW。值得一提的是,压电工作模式的充电时间为10 h左右,10 h后才有稳定的输出,而单一电磁工作模式达到稳定输出充电时间为0.75 h。另外,复合式能量收集装置在外接负载的情况下,由于线圈电磁阻尼的存在使得振动幅度略有下降,会带来压电电压幅值的下降,从而功率也有一定的降低,故复合式能量收集装置的最优负载功率略低于单一电磁和压电工作模式的功率之和。
4 结 论
压电与电磁复合发电系统整合了压电和电磁能量收集技术,可以有效地提高能量收集密度。当共振频率达到18 Hz时,复合能量收集装置达到最大负载功率3.8 mW, 相比于采用单一的电磁技术时的最大负载功率3.2 mW,功率增加了19 %。很多传感器或IC在99 %的时间下都是处于睡眠模式,只需要很微弱的电流,所以,复合俘能器绝大部分时间都处在充电状态,只需在发送信号时才工作。该应用电路使用元器件少,成本低,体积少,如果使用贴片元件,可进一步实现微型化。
[1] Anton S R,Sodano H A.A review of power harvesting using piezoelectric materials(2003—2006)[J].Smart Materials & Structures,2007,16(3):R1-R21.
[2] Williams C B,Yates R B.Analysis of a micro electric generator for micro systems[J].Sensors and Actuators:Physical,1996,52(1-3):8-11.
[3] Ng T H,Liao W H.Feasibility study of a self-powered piezoelectric sensor[C]∥Proceedings of SPIE on Smart Structures and Materials 2004:Smart Electronics,MEMS,BioMEMS, and Nanotechnology,San Diego,USA,2004:377-388.
[4] Hibbeler R C.Mechanics of materials[M].USA:Pearson Prentice Hall Publisher,2005.
[5] 单小彪,袁江波,谢 涛,等.悬臂梁单晶压电振子发电的理论建模与仿真[J].浙江大学学报,2010,44(3):528-532.
[6] 阚君武,唐可洪,王淑云,等.压电悬臂梁发电装置建模与仿真分析[J].光学精密工程,2008,16(1):71-75.
[7] 赵兴强,温志渝.基于压电材料的振动能量收集器的谐振频率调节[J].压电与声光,2013,35(2):241-244.
[8] Beer F P,Johnston E R,Eisenberg E R.Vector mechanics for engineers[M].USA:McGraw-Hill Publisher,2004.
[9] Yu Hua,Zhou Jielin,Deng Licheng,et al.A vibration-based MEMS piezoelectric energy harvester and power conditioning circuit[J].Sensors(Switzerland),2014,14:3323-3341.
[10] Jiang S,Li X,Guo S,et al.Performance of a piezoelectric bimorph for scavenging vibration energy[J].Smart Materials and Structure,2005,14:769-774.
[11] Kulah H,Najafi K.Energy scavenging from low-frequency vibrations by using frequency up-conversion for wireless sensor applications[J].IEEE Sensors Journal,2008,8(3):261-268.
[12] 韩权威,李 坤,严 玲,等.磁场增强压电悬臂梁振动发电装置[J].压电与声光,2011,33(1):85-88.
宋隽炜,通讯作者,E—mail:1290391324@qq.com。
Sensor self-powered technology research based on vibration energy harvesting
SONG Yu, SONG Juan-wei
(College of Computer Science and Engineering,Changchun University of Technology,Changchun 130012,China)
Composite energy harvesting technique is a self-powered sensor technology based on piezoelectric and electromagnetic energy harvesting technology.Analyze composite energy harvesting system,put forward mathematical models and discuss relationship between resonance frequency of system and system configuration parameters;design a set of piezoelectric and electromagnetic energy harvesting device,and experimental verification is cavried out.Results show that the given math model is close agreement with output characteristics of system.Under the resonance frequency of 18 Hz,the maximum of load power of the composite harvester achieves 3.8 mW which is increased by 19 % compared with 3.2 mW of the single electromagnetic technique.
ambient vibration; energy harvesting; piezoelectric energy conversion; electromagnetic energy conversion; wireless sensor
2015—06—29
10.13873/J.1000—9787(2015)09—0013—04
TM 919
A
1000—9787(2015)09—0013—04
宋 宇(1969-),男,吉林省长春人,副教授,主要研究方向为嵌入式系统设计与研究。

