关于范德蒙行列式计算类型的探讨及其运用
关于范德蒙行列式计算类型的探讨及其运用
黄 威1,吕维东2
(1.咸宁市青龙山高中,湖北 咸宁 437005;2.咸宁高中,湖北 咸宁 437005)
范德蒙行列式是法国数学家范德蒙首次提出的,在行列式的计算中,范德蒙行列式由于其独有的特质被人们所吸引,也因为其简单好记的结果受到了很多学者的关注,对范德蒙行列式的研究不仅仅只是在行列式计算中,在其它方面也有广泛的地方。
定义:称行列式
为n级范德蒙(Vandermonde)行列式。
一、范德蒙行列式在行列式计算中的应用
对于某一缺行或是缺列的范德蒙行列式可以通过加边法将其转化成范德蒙行列式再进行计算,对于某些行列式也可以通过分别提取各行或是各列的公因式从而转化成范德蒙行列式。
例1 计算行列式


二、范德蒙行列式在多项式中的应用
在多项式中,有很多问题是关于求根的,而范德蒙行列式运用在多项式求根方面,是会带有一定的便利的,因此熟练的掌握范德蒙行列式对于解决问题能起到关键作用。
例2 对于平面上的任意n个点(xi,yi)(1≤i≤n,xi≠xj,i≠j),证明存在唯一的一个次数不超过n-1次多项式经过该n个点(xi,yi)(1≤i≤n),即有f(xi)=yi。
证明:设f(x)=a0+a1x+a2x2+…+an-1xn-1
又f(x)经过该n个点,所以将这n个点代入得
(1)
将a0,a1,a2,…,an-1看作未知数,则其系数行列式为
由于xi≠xj,i≠j时,所以D≠0,从而方程组⑴有唯一解b0,b1,b2,…,bn-1,即存在唯一的次数不超过n-1次的多项式f(x)=b0+b1x+b2x2+…+bn-1xn-1经过该n个点。
三、范德蒙行列式在向量空间中的应用
向量空间中的有些问题需要通过范德蒙行列式进行转化,才能比较方便的解决问题,下面就举一范德蒙行列式在向量空间中的应用的例子.
例3 设V是数域F上的n维向量空间,任给正整数m≥n,则在V中存在m个向量,其中任取n个向量都线性无关。
证明:因为V是数域F上的n维向量空间,所以只需在Fn中考虑即可,即证明在V中任意n个向量线性无关。
取:
b1=(1,3,32,33,…,3n-1)
b2=(1,32,(32)2,(33)2,…,(3n-1)2)
b3=(1,33,(32)3,(33)3,…,(3n-1)3)
…………
bm=(1,3m,(32)m,(33)m,…,(3n-1)m)
则对于这m个向量中的任意n个向量:
bk1=(1,3k1,(32)k1,…,(3n-1)k1)
bk2=(1,3k2,(32)k2,…,(3n-1)k2)
…………
bkn=(1,3kn,(32)kn,…,(3n-1)kn)
其中1≤k1 若要证明这n个向量线性无关,则需证明对任意的数m1,m2,…,mn,当m1bk1+m2bk2+m3bk3+…+mnbkn=0时,m1=m2=…=mn=0 从而可知这n个向量线性无关,得证。 在微积分中,某些问题如果引用范德蒙行列式及其结果能起到事半功倍的效果。 例4 设f(x)至少有n阶导数,且对某个实数l有 其中f(0)(x)表示f(x)。 解:由泰勒公式可知 (2) 其中x 的线性方程组,其系数行列式为 由于D≠0,所以对于方程组⑵有唯一解,即f(1)(x),f(2)(x),…,f(n-1)(x)可由f(x+a)(a=1,2,…,n)与f(n)(ya)(a=1,2,…,n)线性表示。 又因为 对任意的x<ξ 所以得: 又因为: f(1)(x),f(2)(x),…,f(n-1)(x)可由f(x+a)(a=1,2,…,n)与f(n)(ya)(a=1,2,…,n)线性表示。 所以有: 因此通过对范德蒙行列式的运用在保证能够编码的情况下还能提高它的安全性。这就是范德蒙行列式在非数学方面的充分运用,它不仅能帮助人类有效解决问题,也能给人类带来方便和利益。 [1]徐杰.范德蒙行列式的应用[J].科技信息,2009,(17). [2]刘世界,刘坤.改进的递推公式法及类似范德蒙行列式的计算方法[J].甘肃科技,2013,29(22). [3]程伟健,贺冬冬.范德蒙行列式在微积分中的应用[J].大学数学,2004,20(3). [4]牛海军.范德蒙行列式在行列式计算中的应用[J].中国科教创新导刊,2008,(17). [5]张文治,赵艳.范德蒙行列式应用三则[J].北华航天工业学院学报,2007,17(4). [6]何江妮.范德蒙行列式的证明及其应用[J].黑龙江科技信息,2012,(13). [7]张毅.范德蒙行列式的应用探讨[J].长江大学学报(自然版),2011,8(8). 2095-4654(2015)10-0202-03 2015-06-05
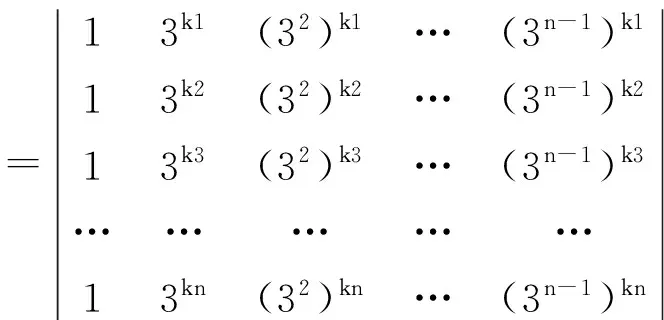
四、范德蒙行列式在微积分中的应用




