缺陷漏磁场磁偶极子模型的若干解析解

时朋朋

（1.西安电子科技大学 机电工程学院，西安 710071；2.西部灾害与环境力学教育部重点实验室 兰州大学，兰州 730000）

无损检测技术是在不损伤构件结构和完整性的前提下，检测构件的某些物理性能和组织状态。检测构件的内在或表面缺陷，评定化学成分、内部组织、力学性能的变化，进而对其适用性进行评价的工艺技术，又称非破坏性检测技术。

铁磁材料被磁化后，其表面和近表面缺陷在材料表面形成漏磁场，通过检测漏磁场来评价缺陷的无损检测技术称为漏磁检测。漏磁检测技术通常测量垂直和平行于缺陷表面的漏磁场分量，来实现对缺陷的定量分析。基于试验或仿真方法建立缺陷和漏磁场信号间的定量关系，是实现缺陷定量分析的基础。

缺陷漏磁场可由不同的模型描述，学者们对漏磁场的研究方法主要有磁偶极子法［1］和有限元法［2］，其中磁偶极子模拟方法利用静磁学可以简单直观地计算磁偶极子在空间任意点的场强，对解决磁性检测中的诸多理论难题具有异常方便和独特的效果。1966 年ZATSEPIN 和SHCHERBININ最早发表了定量分析缺陷漏磁场的论文，提出用磁偶极子、无限长磁偶极线来模拟工件表面的点状缺陷、浅缺陷和深缺陷。此后，对缺陷漏磁在理论上的分析继续不断深入。SHCHERBININ 和PASHAGIN［3］在1972年给出具有矩形截面的三维裂纹的磁偶极子模型。1986 年EDWARDS 和PALMER［4］使用矩形槽逼近的方案给出半椭圆形槽和漏磁信号的解析解。1998 年MANDALY 和ATHERTON［5］分析了钢管表面环向应力对漏磁信号的影响。为了分析不同缺陷形貌对漏磁信号的影响，2003年MANDACHE 和CLAPHAM［6］计 算了单个圆柱缺陷、相邻圆柱缺陷、跑道缺陷等的表面漏磁场。2011年Le［7］等计算了小口径管道中的空心缺陷的表面漏磁场。我国学者对磁偶极子理论的研究一直比较活跃，对世界无损检测领域作出了突出贡献。近年来，华中科技大学的杨叔子、康宜华等人［8－9］在漏磁场数值模拟、信号处理等方面做了大量研究。仲维畅［10－12］对有限长、无限长带偶极子的漏磁场分布进行研究，分析了漏磁场的轴向分量、法向分量的等强度线。王正道等人［13］利用磁偶极子模型分析了铁磁材料表面应力集中等引起的自发磁记忆信号。磁偶极子模型能很好描述裂纹缺陷处的漏磁场分布特征，与试验结果较为吻合。但是，磁偶极子模型存在一些不足：（1）无法定量磁荷密度的分布形式；（2）适用于强间断面，对位错、夹杂、滑移剪切带等微观损伤不适用；（3）无法考虑结构与材料磁参数的非均匀性［14］。近年来，在计算机技术和数值分析方法支持下，有限元分析方法得以飞速发展，成为解决各类工程分析计算问题的有效途径之一。杨理践等人［15］应用ANSYS 对由励磁单元和探测单元组成的漏磁检测装置进行三维有限元模型仿真分析，验证了钢板厚度增加造成的磁场不饱和现象。康宜华等人［16］运用有限元法分析不同磁化方法对钢丝绳磁化效果的差异，探讨穿过式磁化器中各项几何参数的变化对于钢丝绳内部磁场和缺陷漏磁信号的具体影响。李伟等人［17］对不同形状裂纹漏磁场进行有限元仿真分析，得出了裂纹形状对漏磁场的影响。戴光等人［18］应用ANSYS软件对圆筒形容器漏磁内检测进行仿真分析，分析了缺陷尺寸、容器壁厚、内、外壁缺陷等影响缺陷漏磁信号的因素。

试验研究和有限元仿真结果表明缺陷的复杂形状直接影响其漏磁信号，但是目前磁偶极子模型的研究中常将缺陷简化成矩型或环型凹槽。偶极子模型的研究中，漏磁信号常常表现为沿缺陷形成的磁荷面的定积分，由于被积函数复杂性，很多定积分不能用已知的积分公式得到精确值。当选取特殊的缺陷形貌进行研究，并且假设磁荷是均匀分布的，描述漏磁信号的定积分可以进一步得到使用起来更加方便的解析表达式。目前为止，已获得的漏磁信号的解析解屈指可数。笔者利用磁偶极子模型获得了梯型、矩型、V 型和组合型凹槽缺陷表面漏磁信号的解析解。得到的矩形凹槽表达式和已有经典文献结果一致，梯型和组合型凹槽的表达式为首次获得，V 型凹槽表达式与文献［19］存在差异。同数值积分结果的对比证实获得的解析表达式的正确性。

1 磁偶极子模型

磁偶极子理论认为缺陷的漏磁场由极性相反的偶极子产生。所谓磁偶极子是指一对异种等量点磁荷组成的磁性体系。当磁化后的铁磁性试件表面存在孔洞、凹坑、点状压痕缺陷时，缺陷两侧会有磁力线泄漏出工件，在磁力线离开工件缺陷一侧处和进入工件缺陷另一侧处将形成很小的磁极。这些很小的磁极可近似认为是一对极性相反的等量磁荷，即可用等效偶极子模型来模拟。

考虑如图1所示的线偶极子模型，假设存在两条符号相反、线磁荷密度ρm相等、相距为2b、沿垂直于x－y平面方向无限长的两条磁荷线，正负磁荷线在与它们相距r1和r2的点产生的磁场分别为线偶极子在空间P点的磁场H为H1和H2的矢量和，磁场H沿x，y方向的分量分别为

图1 线磁偶极子模型

式中：Hx和Hy场分别为线磁偶极子在P点产生的磁场H的分量x和分量y，μ0＝4π×10－7H／m为真空磁导率。

2 缺陷形状

缺陷的复杂形状直接影响其表面漏磁信号的大小、分布等，基于磁偶极子模型可以针对不同的缺陷形状分析其对应漏磁场信号特征，进而建立缺陷检测评价依据。这里考虑缺陷具有四种不同的端面形状，分别为梯型凹槽、矩型凹槽、V 型凹槽和组合型凹槽。图2依次给出四种缺陷的截面图，缺陷沿垂直于xy平面方向无限长，缺陷左右两侧形成符号相反，面磁荷密度ρs相等的两个磁荷面。梯型凹槽截面呈梯型，2a为凹槽底端的宽度，2a＋2b为凹槽顶端的宽度，凹槽的深度（即凹槽底端与表面距离）为h。矩型和V 型凹槽可以看作梯型凹槽的特例，当梯型凹槽形状参数b＝0和a＝0的时候，梯型凹槽可以依次退化得到矩型和V 型凹槽。组合型凹槽缺陷如图2（d）所示，假设缺陷沿垂直于x－y平面方向无限长。组合型凹槽顶部为梯型凹槽，其底端长度为2a，顶端长度为2a＋2b，高为h－d。组合型槽底部为V 型凹槽，其底端长度长度为2a，深度为d。如图2（d）所示，组合型槽缺陷漏磁场的计算可以归结为V 型凹槽和梯形凹槽的组合运算。图中星形所在直线为缺陷的磁荷面，星形代表分布磁荷。

3 缺陷漏磁场解析解

鉴于矩型、V 型和组合型凹槽可看作梯型凹槽的变形或组合，故先分析梯型凹槽漏磁信号的解析表达式，进而利用梯型凹槽漏磁信号的解析表达式依次获得其余缺陷漏磁信号的解析表达式。

3.1 梯型凹槽

如图2（a）所示，设磁化使梯形凹槽两侧壁形成两个磁荷面，磁荷面方程为x＝－by／h－b－a和x＝by／h＋b＋a。假设磁荷面均匀分布极性相反密度相等的面磁荷，并设在槽口和其他部位均无磁荷分布。那么左右两侧槽壁上以深度η为中心、宽为dη、磁荷密度为ρs的面磁荷在空间任何一点P（x，y）所产生的磁场为：

磁场强度分量Hx和Hy可对dHx＝dH1x＋dH2x和dHy＝dH1y＋dH2y沿缺陷深度积分求出：

图2 四种缺陷的截面图

式中：ρs为磁荷密度。

3.2 矩型凹槽

令梯型凹槽漏磁信号的解析表达式中b＝0，得到矩形凹槽漏磁信号的解析表达式。空间任何一点P（x，y）磁场强度分量Hx和Hy分别为：

3.3 V 型凹槽

令梯型凹槽漏磁信号的解析表达式中a＝0，得到V 型凹槽漏磁信号的解析表达式。空间任何一点P（x，y）磁场分量Hx和Hy分别为：

3.4 组合型凹槽

如图2（d）所示，设磁化使梯形凹槽两侧壁形成两个磁荷面。端部为V 型凹槽左右磁荷面所在斜线方程为x＝－ay／d－ah／d和x＝ay／d＋ah／d。如图3所示，组合型槽缺陷漏磁场的计算可以归结为V型凹槽和梯形凹槽的组合运算。图中原点所在直线为缺陷的磁荷面。空间任何一点P（x，y）磁场分量Hx和Hy分别为：

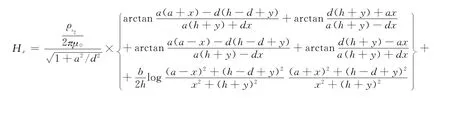
式中：ρs1为组合型缺陷底部V 型凹槽的磁荷密度；ρs2为组合型缺陷顶部梯型凹槽的磁荷密度。

4 比较与验证

矩型、V 型和组合型凹槽漏磁信号解析解是梯型凹槽解析解的直接变形或组合，所以鉴于篇幅所限，仅对梯形凹槽漏磁信号数值解和解析解进行详细的比较。得到的矩形凹槽表达式和已有经典文献结果一致，梯型和组合型凹槽的表达式为首次获得，V 型凹槽表达式与文献［19］存在差异，通过同数值积分结果进行对比证实获得的解析表达式的正确性。

4.1 梯型凹槽

图3 组合槽的分解算法

观察公式（3）和（4）知漏磁信号分量Hx和Hy是对dHx＝dH1x＋dH2x和dHy＝dH1y＋dH2y沿缺陷深度做定积分求得的。由于缺陷形貌的特殊性和磁荷均匀分布的假设，此处获得漏磁信号的解析解。由于被积函数复杂性，很多定积分不能用已知的积分公式得到精确值。这时，利用数值积分可以快速而有效地计算复杂的积分。形如定积分，当被积函数f（x）光滑连续时，其数值解可借助复 化梯形 公式实 现≈。这 里n表示计算中将区间a，［］b划分为n等份，在每个小区间上应用梯形公式计算定积分，然后将其结果相加。定义I为精确解，Tn为将区间a，［］b划分为n等份时复化梯形公式得到的数值解，复化梯形公式的误差为

通过将缺陷漏磁信号解析解与复化梯形公式得到的数值解进行比较验证结果的正确性。计算取缺陷尺寸a＝0.5mm，b＝0.5mm，缺陷深度h＝0.5mm，提离高度y＝0.5mm。ρs＝4πμ0δs，δs。这里磁荷密度ρs的选取参考了文献［19］的做法。表1给出梯形凹槽漏磁信号数值解和解析解的比较。由表1可以发现数值积分参数n＝100时，数值积分解和解析解误差在1%以内，有着极好的精度。在以后数值积分求解过程中使用n＝100。此外，数值积分解和解析解的一致性一定程度说明解析表达式的正确性。图4模拟了梯形凹槽缺陷表面漏磁信号，计算中取缺陷特征尺寸a＝1mm，b＝0.5mm，缺陷深度h＝1mm，2mm，3mm，提离高度y＝1mm。取磁荷密度ρs＝ 4πμ0δs，δs＝，Ha＝60 A／m，μ0＝4π×10－7H／m，μ＝7 000。从图4可以看出，若缺陷尺寸以其中轴是对称的，则缺陷漏磁信号x方向分量Hx以中心点是偶对称的；缺陷漏磁信号y方向分量Hy显示出以中心点是奇对称的大小相等的正负双峰结构。此外裂纹漏磁场大小随裂纹深度的增加而逐渐增大。这些模拟结果均与漏磁场信号的基本特征保持一致。此外，数值积分解和解析解的一致性一定程度说明解析表达式的正确性。

表1 梯形凹槽漏磁信号数值解和解析解的比较

图4 不同缺陷深度下梯型凹槽缺陷的漏磁信号分布

4.2 矩型凹槽

矩形凹槽漏磁信号Hx的解析表达式与Zatsepin和Sheherbinin［1］给出的表达式形式稍有出入，Hy的表达式完全一致，Zatsepin和Sheherbinin给出Hx的表达式为：

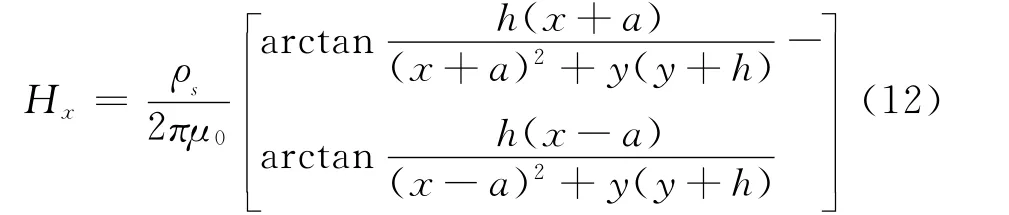
图5给出表达式（5）和表达式（12）计算获得的漏磁信号Hx。计算中取缺陷宽度2a＝2 mm，4mm，6mm，缺陷深度h＝1mm，提离高度y＝1mm，2mm，3mm。取磁荷密度ρs＝4πμ0δs，δs＝，其中Ha＝60A／m，μ0 ＝4π×10－7H／m，μ＝7 000。从图5可以看出两个表达式其实只是形式的差别，结果完全一致。此外还可以看出，漏磁场信号的幅值随提离高度y的增大而迅速减小。

图5 不同提离高度下矩型凹槽缺陷的漏磁信号分量Hx 分布

图6 不同缺陷宽度下V 型凹槽缺陷的漏磁信号分布

4.3 V 型凹槽

笔者得到的V 型凹槽漏磁信号解析表达式与参考文献［19］存在较大差异。通过将缺陷漏磁信号解析解与复化梯形公式得到的数值解进行比较验证结果的正确性。计算中取缺陷宽度b＝1mm，2mm，3mm，缺陷深度h＝1mm，提离高度y＝0.5mm。取磁荷密度，其中Ha＝60A／m，μ0 ＝4π×10－7H／m，μ＝7 000。从图6可以看出，裂纹漏磁场随裂纹宽度的增加而逐渐增大。数值积分解和解析解完全一致，说明解析表达式的正确性。

5 结论

缺陷的复杂形状直接影响其表面漏磁信号的大小和分布，针对具有不同的端面形状的四种凹槽缺陷，以磁偶极子模型为理论基础，给出缺陷漏磁信号的解析表达式，得到的矩型凹槽表达式和已有经典文献一致，梯型和组合型凹槽的表达式为首次获得，V 型凹槽表达式与文献存在差异，通过同数值积分结果进行对比，证实笔者表达式的正确性。

［1］ZATSEPIN N，SHCHERBININ V.Calculation of themagneto static field of surface defects.I.Field topography of defect models［J］.Defektoskopija，1966，5：50－59.

［2］HWANG J，LORD W.Finite element modeling of magnetic field／defect interactions［J］.ASTM J Test Eval，1975，3（1）：21－25.

［3］SHCHERBININ V，PASHAGIN A.Influence of the extension of a defect on the magnitude its magnetic field［J］.Defektoskopija，1972，8：74－83.

［4］EDWARDS C，PALMER SB.The magnetic leakage field of the surface breaking cracks［J］.Journal of Physics D－Applied Physics，1986，19（4）：657－673.

［5］MANDAL K，ATHERTON DL.A study of magnetic flux－leakage signals［J］.Journal of Physics D－Applied Physics，1998，31（22）：3211－3217.

［6］MANDACHE C，CLAPHAM L.A model for magnetic flux leakage signal predictions［J］.Journal of Physics D－Applied Physics，2003，36（20）：2427－2431.

［7］LE M，LEE J，SHOJI T.A simulation of magnetooptical eddy current imaging［J］.NDT ＆ E International，2011，44（8）：783－788.

［8］何利勇，陈厚桂，康宜华.钢丝断口漏磁场磁荷模型定量描述的实验研究［J］.无损探伤，2005，29（4）：22－24.

［9］康宜华，杨克冲，朱文凯，杨叔子.钢丝绳断丝断口漏磁场分析计算［J］.中国机械工程，1993，4（4）：6－8＋4.

［10］仲维畅.20年来中国磁偶极子理论研究进展［J］.无损检测，2000，22（12）：551－554.

［11］仲维畅.工件表面矩形沟槽引起的漏磁场分析［J］.无损检测，2004，26（7）：339－341＋382.

［12］仲维畅.横截面为任意形状的表面开口缺陷的漏磁场［J］.无损检测，2006，28（12）：633－635＋651.

［13］WANG ZD，YAO K，DENG B，etc.Quantitative study of metal magnetic memory signal versus local stress concentration ［J］.NDT ＆ E International，2010，43（6）：513－518.

［14］姚凯.基于金属磁记忆法的铁磁材料早期损伤检测与评价的实验研究［D］.北京：北京交通大学，2014.

［15］杨理践，张森林，高松巍.钢板厚度对漏磁检测效果的影响［J］.无损检测，2013，35（10）：10－13.

［16］康宜华，黎振捷，杨芸，等.微小型钢丝绳漏磁检测传感器与仪器［J］.无损检测，2014，36（5）：11－15.

［17］李伟，左宪章，张云，等.基于脉冲漏磁原理的钢板裂纹缺陷检测有限元分析［J］.无损检测，2013，35（7）：4－7.

［18］戴光，孙立强，杨志军，等.圆筒形容器漏磁内检测ANSYS仿真分析与试验［J］.无损检测，2013，35（3）：25－29.

［19］徐章遂，徐英，王建斌，等.裂纹漏磁定量检测原理与应用［M］.北京：国防工业出版社，2005.