高频疲劳损伤齿轮磁记忆效应的仿真
胥永刚,孙兴芝,崔玲丽,张建宇
(北京工业大学机电学院,先进制造技术北京市重点试验室,北京 100124)
齿轮是机械设备中重要的零部件之一,其工作性能的好坏常会对整个设备产生决定性的影响。特别是在低速重载设备中,当齿轮处于潜在故障状态时,所测得的振动信号和声发射信号常十分微弱,难以得到有效的故障信息。
金属磁记忆检测技术是近年来兴起的一种新的无损检测技术,其利用铁磁材料的磁机械效应,根据试件在工作载荷和地磁场的共同作用下,试件内部产生磁畴组织定向和不可逆的重新取向,在应力集中的区域和缺陷处形成漏磁场,通过检测该漏磁场并根据金属材料的特性做出综合评定[1],能够准确地探测试件应力集中的危险部位[2]。磁记忆检测技术一经提出,迅速在压力容器[3]、汽轮机叶片[4]等领域得到广泛应用,但在齿轮早期故障检测中尚属起步阶段。
应用ANSYS有限元分析软件,对高周疲劳下齿轮磁记忆效应进行了仿真模拟,并与实际的齿轮疲劳试验过程进行对比分析,用以验证仿真过程的正确性,期望为利用磁记忆检测技术对齿轮早期故障进行诊断提供理论依据。
1 金属磁记忆检测原理
金属磁记忆检测是指铁磁性构件在外界拉力或压力载荷和地磁场共同作用下,构件的应力集中区域磁畴组织会发生磁致伸缩性质的定向和不可逆的重新取向,导致构件磁导率不再为常量,进而改变了通过应力集中区的磁场分布,其表面产生漏磁场。磁记忆检测就是通过专用仪器检测构件的表面磁场,分析得出该构件的漏磁场强度HP。若试件内部出现应力集中其磁场强度的计算公式为:

当试件无应力作用时内部的磁场强度计算公式为:

式中:λH表示磁弹性效应的不可逆分量;u0=4π×10-7为真空磁导率;Δσ为机械应力的变化;B为磁感应强度;M为磁化强度;BH为残余磁感应强度;H0为外磁场强度,约为40A/m;uσ为相对磁导率。
在应力集中区域所形成磁场强度Hp的变化曲线如图1所示。其中磁场的切向分量Hp(x)存在最大值,而法向分量Hp(y)改变方向并且具有零值点。工程试践中常通过对磁场法向分量Hp(y)的检测来可判断出工件的应力集中区域[5]。俄罗斯动力诊断公司的应力集中检测仪采用法向分量Hp(y)过零点和梯度值两个关键特征量来进行诊断分析。

图1 磁记忆检测原理
2 高周疲劳下齿轮磁记忆仿真分析
为了明晰齿轮局部应力集中与磁记忆效应之间的规律,首先运用ANSYS软件对某一齿轮在高周疲劳下的磁记忆效应进行了仿真分析。
为了与后期试验保持一致,仿真分析所用齿轮的具体参数为:齿轮的材料为20CrMnTi渗碳钢,模数为5mm,齿数为30,分度圆直径为150mm,齿根圆直径为137.5mm,齿顶圆直径为160mm。
2.1 齿轮的应力场分析
2.1.1 建立几何模型和网格划分
首先,根据齿轮的相关参数,在ANSYS平台上建立了齿轮三维实体模型,并在第7齿预设了裂纹缺陷,所使用的单元类型为3-D SOLID95,然后对其进行网格划分,裂纹尖端点采用KSCON 命令建立奇异点[6],裂纹处的有限元网格模型如图2所示。

图2 裂纹处的有限元网格模型
2.1.2 施加约束条件和载荷
根据试验室环境的要求设置相应的参数,对有裂纹的第7齿和第26齿施加了20.57kN 均布力,对齿轮内圈的下表面施加全约束。在求解过程当中选用双线性等向强化模型,并且开启大变形效应进行非线性分析。加载后的等效应力图如图3所示。

图3 齿轮的等效应力图分布
2.1.3 提取测点路径的应力值
鉴于齿轮模数较小,后期试验只能沿齿轮端面齿根部圆周方向测量,故仿真分析中亦沿着图3所示的路径拾取该路径上的应力值(路径的起点为第1个齿轮),构成应力值分布曲线如图4所示,图中横坐标为假想传感器移动的位移,单位为mm,纵坐标为对应的应力值。从图中可以明显的看出第7齿和第26齿出现了应力集中现象。

图4 沿所取路径的应力值分布
2.2 应力与磁化强度的关系
由式(2)可知,当齿轮不受外力作用时,齿轮的磁场强度受到磁化强度的影响。当在静磁场中模拟正常齿轮磁场强度时,需要得到齿轮在不受外力作用时的磁化强度值M。
通过Langevin定律的磁化规律可以得到:

式中:He为有效外磁场强度;a为有效场因子;M为磁场强度;Ms为饱和磁化强度;L(x)为Langevin函数。
在应力σ和地磁场H的共同作用下,铁磁试件的有效场He可以表示为:

式中:βM为磁畴场;Hσ为磁畴间的磁弹性相互作用,是由外应力所引起的等效应力场。
依据热力学的理论,在应力与磁场同轴的情况下,可以得到以下等式:

式中:G为Gibbs自由能密度;U为内能密度;A为Helmholtz自由能密度;λ为块状物体的磁致伸缩系数。所以,有效场He可以表示为:
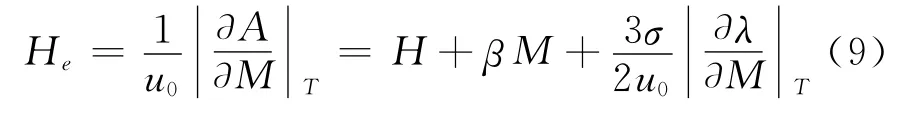
式中磁致伸缩系数λ关于M=0对称,当M较低时,可近似为:

式(10)中系数b为常数,称为磁致伸缩-磁化强度的关联系数,可由试验结果来确定,将式(10)代入(9),可得有效场He为:


将式(11)代入式(12)可得:

式中:a为有效场因子,取a=21 600;b为磁致伸缩-磁化强度关联系数,取b=1.783×10-18;u0表示真空磁导率;Ms为饱和磁化强度,取MS=1.7×106;H为外加磁场强度,取H=40A/m;β为分子场系数,取β=4.182×10-2[7]。
由上式可得,当σ=0时,M=28.985A/mm。
2.3 应力与相对磁导率的关系
铁磁构件相对磁导率的变化与应力有关,当构件受力时,应力集中部分的相对磁导率就会发生改变从而对构件的磁化强度产生影响。
设铁磁试件在没有外力作用(F=0)时,铁磁试件被磁场强度为H的外磁场磁化,并产生磁感应强度B1,因此磁导率为,此时铁磁试件所产生的磁能为:

当外力作用时,铁磁试件的磁感应强度为B2,磁导率,此时铁磁体所具有的磁能为:

则铁磁试件的能量增量为:

当磁化未达到饱和状态时,所产生的单位压磁能量的变化量为:

式中:λ为磁致伸缩系数,根据能量守恒定理,单位体积的磁化功率变化量等于由机械外力所引起的单位磁积能的变化量,即ΔW=-ΔW1。所以

将式

代入式(18)中得

式中:λm为铁磁材料的饱和磁致伸缩系数;Bm为铁磁材料的饱和磁化强度。
从上式可以得到铁磁材料的相对磁导率变化与应力的关系[8]。
根据试验齿轮的材料确定λm跟Bm的数值从而得到试件应力与相对磁导率的关系曲线如图5所示。
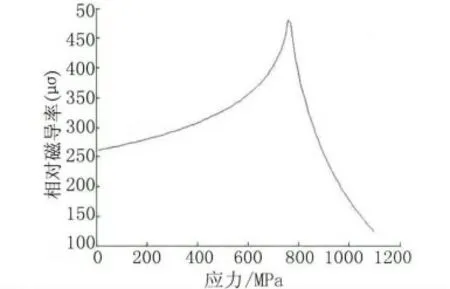
图5 应力与相对磁导率的关系曲线
2.4 静磁场的有限元分析
根据如图4所示的齿轮齿根部圆周方向上的应力曲线,结合图5所示的应力与相对磁导率的关系曲线,对齿轮进行相对磁导率的划分,结果如图6所示。由于铁磁材料的磁化过程与外加磁场具有密切的关系,磁记忆效应所处的磁场强度要求大约为40A/m,笔者使用Plane53单元分别对试件、永磁体、衔铁及空气进行网格划分[9]。该二维模型中空气的相对磁导率为1,不设置矫顽力;永磁体的相对磁导率为1.075 9,矫顽力设置为56A/m;衔铁的相对磁导率为1.86×105。为了让试件周围的地磁信号比较均匀,笔者将使用较大的永磁体模型,其尺寸为1 000mm×1 000mm,间距为500mm。整体的模型使用二维平面模型的方式建模,如图7所示。
将正常齿轮跟划分好相对磁导率的带有裂纹的齿轮分别放入图7所示的磁场中,对边界施加约束条件并求解可以得到齿轮内部磁感应强度的分布,并确定图3所示路径相对应的磁感应强度B,从而求出相应的磁场强度Hp,如图8所示。

图6 齿轮相对磁导率的划分

图7 二维磁场平面模型

图8 二种状态下齿轮的磁记忆仿真信号
3 齿轮磁记忆检测试验
试验用齿轮具体参数如前所述,齿轮如图9(a)所示。检测所用的仪器为俄罗斯动力诊断公司所生产的应力集中磁检测仪TSC-1M-4,使用具有小轮的磁记忆传感器顺着齿根圆周测量磁记忆信号,探头的位置如图9(b)所示。

图9 齿轮及探头位置
3.1 正常齿轮磁记忆检测
第一步对正常齿轮进行磁记忆的检测,所得的结果如图10所示。图10(a)表示磁记忆传感器沿路径连续测量5周(单周采样点数为390)所得原始磁记忆信号。对上述磁记忆信号进行平均,得到如图10(b)所示单周磁记忆信号。

图10 正常齿轮磁记忆信号
3.2 含裂纹齿轮的磁记忆检测
将齿轮安装到QBG-100 高频疲劳试验机上[10]。在试验室环境中设定相关参数为:平均负荷为-20.57kN;动态幅值为18.65kN;齿轮共振频率为148Hz;受载齿为第7,26齿。
使第7齿和第26齿为受载齿,加载20min后,第7齿齿根部开始产生明显的裂纹并慢慢的扩展,此时共振周次为457×100次。如图11所示。停止疲劳试验机,卸除静态载荷,拿下齿轮并用仪器现场测量磁记忆信号。

图11 含裂纹齿轮
图12(a)表示连续5周所测量的齿轮磁记忆信号,从波形中可以看出明显的突变成分,位置大概在在第7齿和第26齿上。图12(b)表示平均后的单周磁记忆信号,通过与图3的比较,可以明显看出第7齿和第26齿齿根部的磁场强度存在明显的变化,受载齿所处位置得磁场强度明显较高。第7齿磁场强度明显变化的原因是因为齿根处出现裂纹,应力集中比较明显。第26齿虽然没有产生裂纹,但是在试验的过程中该齿也受应力作用,也产生了应力集中现象,因此磁记忆信号也出现了明显变化[11]。
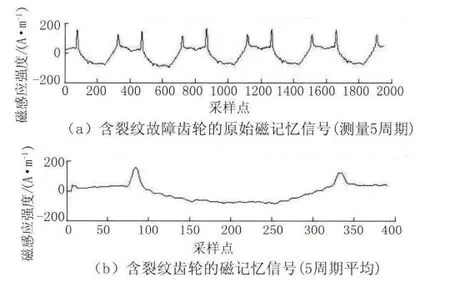
图12 含有裂纹的齿轮磁记忆信号
将图8(a)和图10(b)、图8(b)和图12(b)进行比较可以发现,正常齿轮和含裂纹故障齿轮磁记忆仿真信号和高周疲劳试验下测取的试际磁记忆信号相似度很高,证明了仿真过程的正确性和磁记忆检测试验的有效性,同时也证明了文献[11]中“齿轮磁记忆信号的总体趋势是向负值方向单调下降然后向正值方向单调上升,该变化趋势与齿轮的圆形形状有关”这一论断。
4 结论
通过ANSYS有限元分析软件对齿轮磁记忆检测试验进行模拟,将得到的理论结果跟检测试验所得到的结果进行对比,说明利用金属磁记忆技术对齿轮潜在故障的进行诊断的方法是可行的。该技术尤其对于肉眼无法观察到明显缺陷的应力集中区域,较之振动信号、声发射信号等常规检测方法有明显优势。
[1]DOUBOV A A.Express method of quality control of a spot resistance welding with usage of metal magnetic memory[J].Welding in the World,2002,46(6):317-320.
[2]汪滨波,廖昌荣,骆静,等.金属磁记忆检测技术的研究现状及发展[J].无损检测,2010,32(6):467-474.
[3]王朝霞,宋金刚,陈克,等.基于金属磁记忆方法的压力容器检测技术[J].压力容器,2006,23(12):42-44.
[4]池永滨,刘宇哲,胡先龙,等.汽轮机叶片金属磁记忆诊断技术[J].无损检测,2002,24(10):440-442.
[5]王丽,冯蒙丽,丁红胜,等.金属磁记忆检测的原理和应用[J].物理测试,2007,25(2):25-30.
[6]瞿伟廉,鲁丽君,李明.带三维穿透裂纹结构的有限元试体建模方法[J].武汉理工大学学报,2008,30(1):87-90.
[7]任尚坤,任吉林,宋凯.铁磁试件的力-磁效应分析和相关参数估算[J].河南师范大学学报,2007,35(1):78-82.
[8]王社良,王威,苏三庆,等.铁磁材料相对磁导率变化与应力关系的磁力学模型[J].西安科技大学学报,2005,25(3):288-291.
[9]YAO K,DENG B,WANG Z D.Numerical studies to signal characteristics with the metal magnetic memoryeffect in plastically deformed samples[J].NDT & E International,2012,47:7-17.
[10]方发胜,周培,张利明,等;疲劳试验下应力集中与磁记忆信号的关系[J].无损检 测,2014,36(3):30-35.
[11]胥永刚,谢志聪,崔玲丽,等;基于ITD 的齿轮磁记忆信号特征提取方法的研究[J].仪器仪表学报,2013,34(3):671-676.

