岩土参数反算在工程应用中的分析
王书剑
(1.长沙理工大学交通运输工程学院,湖南 长沙 410076;2.长沙市公路管理局城郊路政执法大队,湖南 长沙410007)
0 引言
目前用来分析岩土工程稳定性的方法有很多,如数值分析法、极限平衡法等。在对岩土体进行稳定性分析时,准确的强度参数是至关重要的。工程中经常用土工试验来获取内摩擦角φ、黏聚力 c等强度参数。该方法得出的试验结果可靠,且适用于大多数岩土体。但对构造复杂的土体,如碎石土等,若用土工试验来获取其参数,所耗时间长,且难度较大。并且有些土体强度参数的空间变异性较大,得到的试验结果离散,很难得到准确的计算参数[1-2]。在此情况下,通过采用参数反演手段来获取岩土体强度参数已得到广泛的应用[3]。准确分析和评价边坡稳定性的关键是如何正确选取土工参数,进而会影响到边坡工程的安全。而这些土工参数中,滑动面岩土体的重度γ,其选用值的误差对边坡稳定性的影响远小于粘聚力c、内摩擦角φ。因此,滑坡岩土体抗剪强度参数c、φ的取值成为影响边坡稳定性分析结果可靠度的关键,研究确定c、φ值的方法对边坡工程的稳定性分析与加固设计具有重大的实际意义。
1 原理分析
1.1 反算分析法
在国内外边坡稳定性分析通常采用极限平衡条分法,主要有瑞典法、Janbu法、简化Bishop法和传递系数法等,其中传递系数法在滑面边坡的应用最为广泛。传递系数法不计力矩平衡条件,只考虑力的平衡,简单易行,而且与其他极限平衡方法的计算结果相差不大,能基本满足边坡工程实践的需求。反演分析采用的边坡稳定性分析模型不同,反算得到的强度参数值也会有所不同。
1.1.1 反分析基本前提
反演分析的可靠性主要取决于边坡稳定状态和边界条件的准确性。反演分析的基本前提:①结合实际情况选定边坡稳定性系数值;②勘察滑动面位置及滑动形式;③总结分析造成边坡失稳或坡体变形的外力因素。
1.1.2 反分析求解过程
对于确定的滑坡断面,先假定稳定系数Fs已知,利用传递系数法可以求取c、φ值的对应关系。但c、φ值是两个不确定参数,对于单一断面的一个极限平衡方程,c、φ值具有不确定性,必须先假定c或φ中一个,再求解另一个未知数,这样可求出无数组c、φ值的解,但却无法获得反映滑坡滑动时真实状态的唯一解。为了同时反算出c、φ值,可在滑坡体中寻找两个或多个处于极限平衡状态的断面,建立不少于两个极限平衡方程联立求解。通常情况下,为了提高反算结果的可信度,可同时结合土工试验、工程类比或敏感性分析等方法来确定强度参数的取值。
联立滑坡的两个或多个断面进行求解,可能会出现两条或多条平行直线方程的情况,以致无法求解。因此,多断面极限平衡方程联立反算的基本条件是选取的多个滑坡断面必须相似。相似条件包括:①地质条件相似,滑坡的类型和形式、滑带土的物质组成以及含水状态要相似;②滑坡的运动过程和状态相似。
将坡体将滑而未滑那一瞬间视为滑坡的极限平衡状态,在未发生滑动时,其稳定系数Fs=1。采用传递系数法列出滑坡断面的极限平衡方程,求解出多个断面的一系列不同c、φ值组合,釆用图解法绘制多个断面的c-φ曲线,交点即为反算的强度参数值。

图1 c、φ值反分析图解示意图
1.2 基于传递系数法的反算分析
传递系数法(即不平衡推力法)是滑坡稳定性分析使用最广泛的方法之一。传递系数法假定滑坡体为整体滑动,各条块的条间力以集中力表示,作用在分界面中点,其作用方向与上一条块的底面平行。在对滑坡范围内滑动方向和速度大体一致的滑体进行计算时,可将它们视为一个计算单元,并选择其中的典型滑坡断面进行分析。根据不同地层性质和滑面坡度的差异,将整个滑体划分为若干竖直条块。由力的平衡条件可知,从第一个条块连续向前逐条向下推求,直至最后一个条块的推力为零,该方法通常有隐式解法和显式解法两种[4]。传递系数法有三个假定条件:①滑体不可压缩并作整体下滑;②条块间只传递推力不传递拉力;③取垂直滑坡主轴方向单位宽度(一般为1m)的岩土体作为计算断面,不考虑条块两侧的摩阻力[2]。
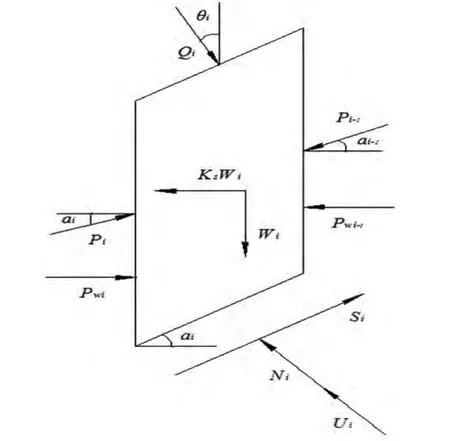
图2 第i个条块受力示意图
取滑坡体的第i个条块为研究对象,条块i的受力图如图2所示。由力平衡条件,可得第i条块的条间力Pi表达式:

其中,

ψi为传递系数,可简化计算为:

上述式子中的c和tanφ均为滑面实际强度参数,强度不再发生变化。采用下滑力超载稳定系数,即下滑力Ti前乘了稳定系数Fs;然而传递系数ψi可简化成一个常数,且与Fs无关。即设Fs=1,由此推出安全系数的显式表达式为:

上式是《公路路基设计规范》中常用的公式。在滑坡处于极限平衡状态下,传递系数ψi的表达式中可假设Fs=1。基于传递系数法进行边坡滑动面强度参数反算分析时,计算量庞大,可利用MATLAB数学软件进行计算,这样可以大大提高计算效率[5]。
2 实例计算
2.1 边坡概况
永龙界ZK56+860~ZK56+940段边坡岩体较破碎松散,覆盖较厚强风化层。边坡开挖成型后,受降雨影响,坡体有两处小面积滑塌,滑带岩土体主要为表层粘土(夹杂少量碎石)、强风化层软岩、泥质页岩等。以下为该路的2处典型滑坡示意图:

图3 1#滑坡体示意图

图4 2#滑坡体示意图ZK56+860~ZK56+940边坡1#、2#滑坡体示意图
该边坡位于断层碎裂带边缘,地质状况复杂,受地质构造及外界条件影响很大,边坡整体稳定性较差。岩质边坡地处断层碎裂带边缘,受地质构造影响显著,岩体完整度较差,块状偏小,岩体风化较严重,抗剪切强度较小。岩体以节理、裂隙发育的强风化砂质页岩和粉质粘土中夹强风化页岩块石两大类为主,强风化层厚度大,岩质较软,整体结构松散。根据现场滑坡的形态特征、滑带岩土体及结构特征和勘探的地质资料,选取ZK56+860~ZK56+940段边坡为研究对象,该处边坡坡体中碎石土较多,土体强度参数的空间变异性较大,对室内直剪试验结果产生较大的离散性,很难获取准确的参数。影响边坡稳定性的因素较多,如岩土体的基本物理力学性质、边坡的几何特征、岩体的结构面参数等。它们对边坡稳定性都有不同程度的影响。由于这些影响因素难以量化,在进行边坡的稳定性分析时,很难考虑到它们的影响。而反算分析方法的思想就是把这些难以量化的因素综合考虑在“等效参数”中,因此采用了基于传递系数法来反算滑动面岩土体的抗剪强度参数,为边坡工程分析发展提出了一种新的方法。
2.2 参数分析
假定边坡处于极限平衡状态,采用传递系数法对ZK56+860~ZK56+940边坡岩土体参数进行敏感性分析。依据勘测资料提供的c、φ取值范围,形成不同的组合系列,利用MATLAB软件计算对应的稳定性系数Fs,计算结果如表1、表3所示。
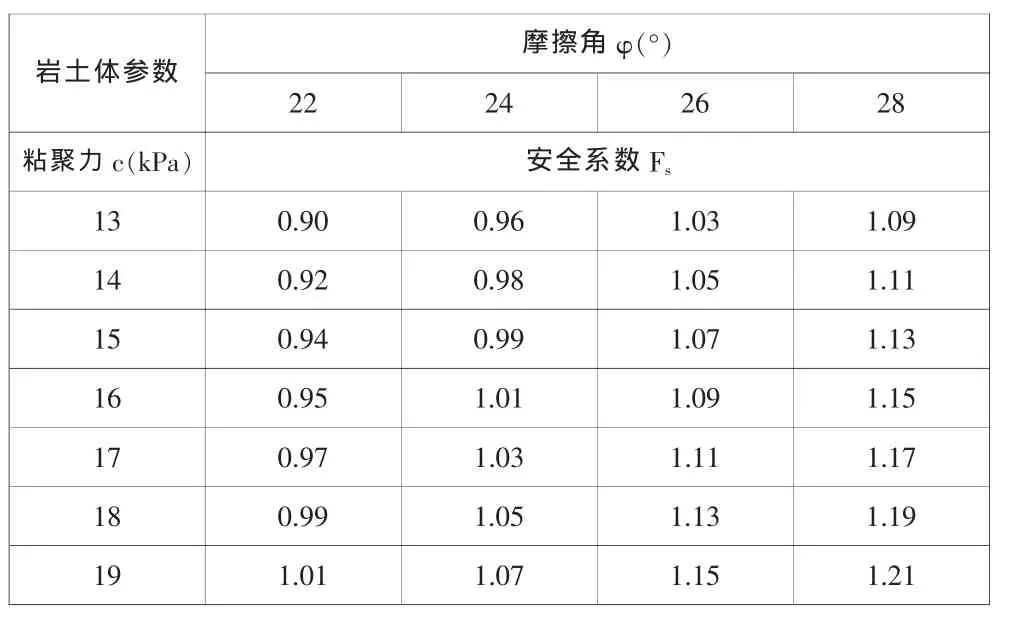
表1 c、φ与Fs的影响关系

图5 Fs-c-φ关系曲线图
由上图可通过拟合曲线得到y=k1x+b公式,得出不同内摩擦角的情况下对边坡稳定性影响的敏感度k1,如下表2所示:
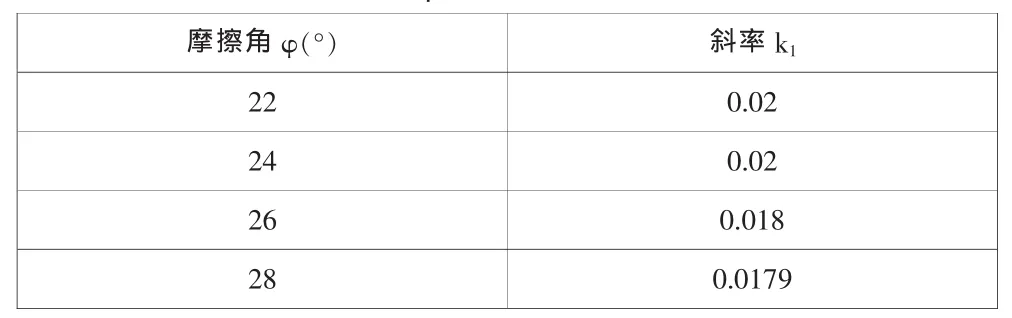
表2 φ与k1的影响关系

表3 c、φ与Fs的影响关系
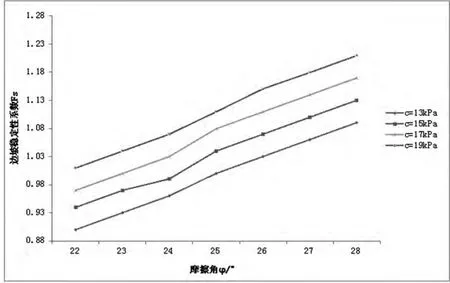
图6 Fs-c-φ关系曲线图
由上图可通过拟合曲线得到y=k2x+b公式,得出不同粘聚力的情况下对边坡稳定性影响的敏感度k2,如下表4所示:

表4 c与k2的影响关系
由图5、图6可知,滑动面岩土体的c和φ值对稳定性系数Fs的影响均较大,比较表2与表4可知,斜率k2>k1,表明对于ZK56+860~ZK56+940边坡滑坡体,稳定性系数Fs对φ值的影响更敏感,且随内摩擦角φ的变大,稳定性系数Fs增加速率更快。因此,在进行反演分析时可先假定c值,然后再通过MATLAB软件的极限平衡稳定分析程序来反算φ值。
2.3 反算参数的确定
根据边坡稳定性传递系数法的稳定系数计算公式,利用MATLAB软件编写了边坡稳定性分析电算程序,考虑 “自重+水”的工况,对ZK56+860~ZK56+940边坡进行滑动面抗剪强度参数c和φ值的反演计算。由以上的边坡参数敏感性分析可知c值的敏感度较低,根据室内试验数据可确定c值的范围,将c值进行区间分段,其中选取c值分别为 13、14、15、16、17、18、19、20kPa, 在滑坡的极限平衡状态及边界条件下,运用传递系数法反算φ值。当稳定系数Fs=1.0时,分别反算出ZK56+860~ZK56+940边坡1#和2#滑坡体在不同c值条件下的φ值。计算结果如表5、6所示。

表5 1#滑坡体传递系数法反算结果

表6 2#滑坡体传递系数法反算结果

图7 1#和2#滑坡体c-φ曲线反演分析
联立ZK56+860~ZK56+940边坡1#和2#两个滑坡体极限平衡方程,求解该边坡滑动面抗剪强度参数反演计算值。如图7中两条c-φ曲线的交点坐标c=15kPa,φ=24.48°即为该边坡滑动面抗剪强度参数反演计算值。
3 结论
本文介绍了获取滑动面岩土体抗剪强度参数的反算分析法,以ZK56+860~ZK56+940边坡两处滑坡体为研究对象,基于传递系数法对该滑坡体的抗剪强度参数进行了反演计算,得到合理参数。通过分析影响边坡稳定性参数内摩擦角φ和黏聚力 c对边坡稳定性的影响得出,内摩擦角φ较黏聚力c对边坡的影响更为敏感。在反演计算中,假定稳定系数Fs=1.0时,分别反算不同c值条件下的φ值,联立两处滑坡体极限平衡状态方程,得出抗剪强度参数为c=15kPa,φ=24.48°,为龙永高速后续边坡开挖施工行为及防护加固时机选择提供指导性建议。
[1]沈永飞.边坡位移反分析及其工程应用研究[D].重庆大学,2010.
[2]童志怡.岩质边坡滑动面力学参数的取值理论和方法研究[D].中国科学院研究生院(武汉岩土力学研究所),2009.
[3]孙志彬.Mohr-Coulomb准则下基于滑动面深度的边坡参数反分析方法[M].岩土力学,2014,4.
[4]贾恒国.抗滑桩设计计算的程序实现[D].太原理工大学,2010,5.
[5]李清.基于极限平衡理论的滑坡抗剪强度参数反演数据表法研究[M].路基工程,2015,4.

