基于奇异观测器的连续系统传感器故障估计*

胡正高, 赵国荣, 马合宝

(1.海军航空工程学院 控制工程系,山东 烟台 264001; 2.海军蚌埠士官学校，安徽 蚌埠 233012；3.91498部队, 河北 秦皇岛 066200)



基于奇异观测器的连续系统传感器故障估计*

胡正高1,2, 赵国荣1, 马合宝3

(1.海军航空工程学院 控制工程系,山东 烟台 264001; 2.海军蚌埠士官学校，安徽 蚌埠 233012；3.91498部队, 河北 秦皇岛 066200)

研究连续系统的传感器故障估计问题，提出一种奇异观测器来进行故障估计，所提方法不需要假设故障、故障导数和干扰的上界已知。通过HB∞性能指标抑制了干扰对故障估计的影响；采用线性矩阵不等式来获得奇异观测器的增益阵；利用Lyapunov泛函得到了观测误差动态系统的鲁棒渐近稳定性；最后通过飞行器仿真实例验证了所提方法的有效性。

故障估计； 奇异观测器； 线性矩阵不等式； Lyapunov泛函

0 引 言

为了维持工业系统的稳定运行与提高生产效率，自动控制系统已经被广泛应用于工业领域。在自动控制系统中，传感器可以为系统的自动控制与监测提供重要信息。为了完成这些任务，传感器的可靠性就变得非常重要。然而，长时间的连续作业会导致传感器的故障，为此，必须尽可能早地检测出故障，让故障对系统造成的损害最小[1]。正是在这样的背景下，故障检测与诊断技术获得了长足的发展，并已经应用到如飞控系统[2]、核反应堆的压力和液位控制系统[3]与火力发电厂中的汽水分离系统[4]等。

与故障检测相比，故障估计的研究更具有理论意义与实际价值，因为通过故障估计不仅可以判断系统是否发生故障，而且可以获知故障的严重程度。相比于执行器故障估计，传感器故障估计的研究相对较少。文献[5]通过独立成分分析方法来估计传感器故障，但需要较长操作时间内的大量数据库才能实现。文献[6]通过状态增广，并设计滑模观测器来估计故障，但是需要假设状态方程中干扰与故障的上界是已知的。文献[7]采用自适应观测器来估计故障，但要求知道故障、故障导数与干扰的上界，然而，在工程实际中并不容易获得这些上界。

针对目前传感器故障估计研究的不足，本文将提出一种奇异观测器来估计传感器故障，利用线性矩阵不等式得到所提观测器的增益矩阵，并采用Lyapunov泛函获得了观测误差动态系统的鲁棒渐近稳定性。在此基础上，得到了传感器故障的鲁棒渐近估计，最后通过一个飞控系统仿真分析验证了所提方法的有效性。

1 问题描述

研究如下状态方法线性连续系统状态方程

(1)

其中，x∈Rn,u∈Rm,y∈Rp分别表示系统的状态、控制输入与测量输出，d∈Rh为外部干扰，f∈Rq为传感器故障。A,B,C,D,F为适维的常值矩阵，其中,F为列满秩矩阵。

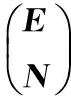
为了简便，后文略去所有向量的时间变量t。定义ζ=[xTfT]T，那么,系统状态方程组(1)变为

(2)

下面,将设计系统状态方程组(2)的奇异观测器，并通过所设计的观测器来实现对传感器故障f的鲁棒渐近估计。

2 奇异观测器设计

考虑系统状态方程组(2)，设计如下的奇异观测器

(3)

令ε=-ζ，由式(3)有ε=-ζ=z-QEζ。对ε求导,可知

(4)

再令

G=L-SR,S=QT-GN,

(5)

那么,式(4)化为

(6)

下面,将利用Lyapunov泛函来证明观测误差系统状态方程式(6)的鲁棒渐近稳定性，并在此基础上实现对传感器故障f的估计。

3 故障估计

定理1考虑系统状态方程组(2)与系统状态方程组(3)，如果存在正定矩阵P、矩阵Y与正数γ使得线性矩阵不等式

Λ=

(7)

成立，那么,观测误差动态系统方程式(6)是鲁棒渐近稳定的，且观测器状态方程组(3)中的待求矩阵分别为G=P-1Y，S=QT-GN，L=G+SR。

(8)

由上可知，若J<0，则定理1得证，下面给出J<0的条件。

对V沿着系统状态方程式(6)求导可得

(9)

令Z=[εTdT]T，由式(9)可知J=ZTΛZ，其中

Λ=

如果Λ<0，那么,J<0。令Y=PG，再根据Schur补定理可知Λ<0等价于式(7)，当式(7)成立时，那么,J<0，从而可知‖ε‖≤γ‖d‖。由式(7)已经计算出矩阵Y，因为Y=PG，所以,G=P-1Y。然后，由式(5)可得S=QT-GN，L=G+SR，至此完成奇异观测器(3)的设计,证毕。

定理2考虑系统(2)与系统(3)，如果存在正定矩阵P、矩阵Y与正数γ使得线性矩阵不等式(7)成立，那么,=[0Iq]是传感器故障f的鲁棒渐近估计。

4 仿真分析

研究某型民航飞机的纵向运动方程P[8]，系统状态方程组(1)中的矩阵分别为

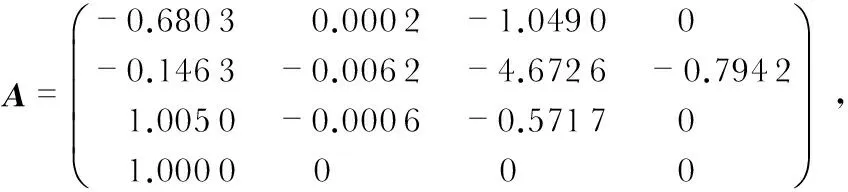
状态x=[x1,x2,x3,x4]T=[q,Vtas,α,θ]T;状态分量q为俯仰角速率,rad/s;Vtas为真空速,m/s;α为攻角,rad;θ为俯仰角,rad。系统(1)的干扰设为d(t)=0.6cos 4t。考虑系统状态方程组(1)的传感器发生如下故障

通过求解线性矩阵不等式(7)的可行解得到γ=0.18，对应的矩阵为

从而根据定理1计算得到矩阵G,S与L。系统状态方程组(1)的初始状态假设为x=[0 195 0.03 0.02]T，观测器状态方程组(3)的初始状态为z=[0 0 0 0 0]T。系统状态方程组(1)的状态估计如图1、图2所示，可以看出，设计的奇异观测器能快速逼近系统状态方程组(1)的状态。传感器的故障估计结果如图3～图5所示，从中可以看出:本文所提出的基于奇异观测器的故障估计方法可以实现对系统中传感器故障的鲁棒渐近估计。

图1 俯仰角速度估计

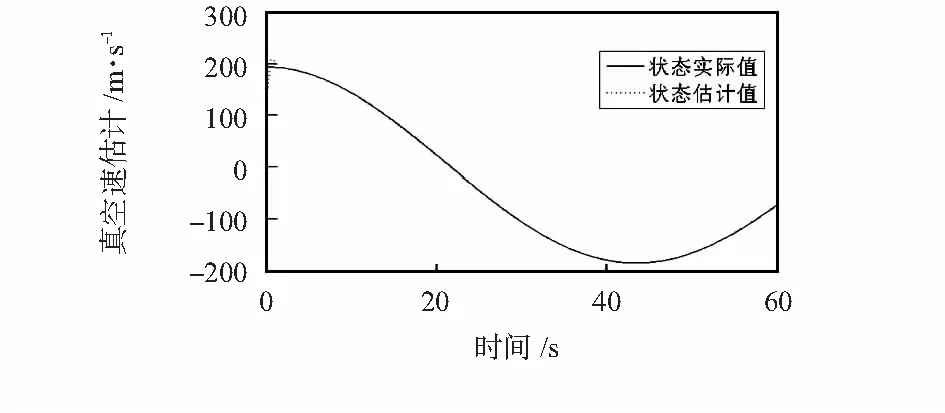
图2 真空速估计

图3 攻角估计

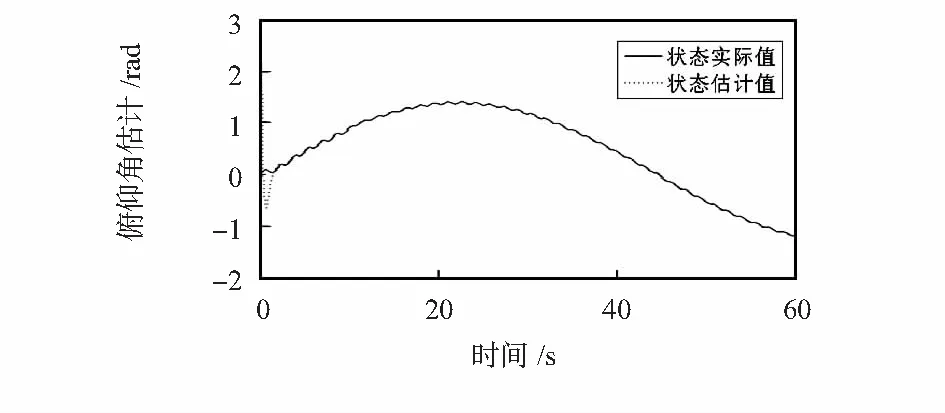
图4 俯仰角估计

图5 传感器故障估计

5 结 论

本文通过设计奇异观测器得到了连续系统中传感器故障的鲁棒渐近估计；利用线性矩阵不等式获得了所提观测器的增益阵；所提观测器不需要对故障、故障导数与干扰作上界已知假设，因此,与已有方法相比，本文的方法适用范围广。仿真分析验证了所提方法的有效性。

[1] 帕孜来·马合木提,董小亮,杨 莲,等.新型解析冗余关系法在传感器故障诊断中的应用[J].传感器与微系统,2014,33(7):157-160.

[2] Hajiyev C.Tracy-widom distribution based fault detection approach:Application to aircraft sensor/actuator fault detection[J].ISA Transactions,2012,51(1):189-197.

[3] Baraldi P,Cammi A,Mangili F,et al.An ensemble approach to sensor fault detection and signal reconstruction for nuclear system control[J].Annals of Nuclear Energy,2010,37(6):778-790.

[4] Aldian Ambark Shashoa N,Kvašcˇev G,Marjanovic＇ A,et al.Sensor fault detection and isolation in a thermal power plant steam separator[J].Control Engineering Practice,2013,21(7):908-916.

[5] Kim M J,Liu H,Kim J T,et al.Sensor fault identification and reconstruction of indoor air quality (IAQ) data using a multivariate non-Gaussian model in underground building space[J].Energy and Buildings,2013,66:384-394.

[6] Alwi H,Edwards C,Tan C P.Sliding mode estimation schemes for incipient sensor faults[J].Automatica,2009,45(7):1679-1685.

[7] Zhang C,Liu X,He J.Robust sensor fault reconstruction for nonlinear systems using observers[J].International Journal of Bifurcation and Chaos,2012,22(2):12500311-12500317.

[8] Zhang K,Jiang B,Shi P.Observer-based fault estimation and accomodation for dynamic systems[M].Berlin,Heidelberg:Springer,2013:20-21.

Sensor fault estimation for continuous system based on descriptor observer*

HU Zheng-gao1,2, ZHAO Guo-rong1, MA He-bao3

(1.Department of Control Engineering,Naval Aeronautics and Astronautics University,Yantai 264001,China;2.Naval Bengbu Petty Officer School,Bengbu 233012,China;3.Army of 91498,Qinhuangdao 066200,China)

The sensor fault estimation problem for continuous system are studied,a descriptor observer is proposed to employ fault estimation,and the proposed method doesn’t need assuming that faults or faults derivative and upper bound of disturbance should be known.The influence to fault estimation caused by disturbance is suppressed by theHB∞performance index;linear matrix inequality is utilized to obtain the gain matrices of the descriptor observer;the robust asymptotically stability of the observer error dynamic system is derived by Lyapunov function;finally,an aircraft simulation example is exploited to illustrate the effectiveness of the proposed method.

fault estimation; descriptor observer; linear matrix inequality; Lyapunov function

2015—01—20

国家自然科学基金资助项目(61473306)

10.13873/J.1000—9787(2015)09—0048—03

TP 272

A

1000—9787(2015)09—0048—03

胡正高(1986-)，男，安徽庐江人，博士研究生，研究方向为动态系统的故障诊断。