基于置信隶属度的多传感器数据模糊融合*

何 明

(江西财经大学 信息管理学院,江西 南昌 330032)



基于置信隶属度的多传感器数据模糊融合*

何 明

(江西财经大学 信息管理学院,江西 南昌 330032)

在数据的融合过程中，将每个传感器的数据看成服从正态分布，利用置信水平得到隶属度，构造优越性比较矩阵，进而得到融合后的数据，将该方法运用于实证，并与平均权、概率权等方法进行比较，实证部分验证了该方法的实用性，再进行多次仿真，通过绝对误差的比较，验证了此方法的稳定性和有效性。

多传感器; 隶属度; 优越性； 比较矩阵; 置信度

0 引 言

数据融合的方法有很多种，多传感器信息融合技术不论在军事领域还是在民事领域都受到了广泛的关注 。这一技术正广泛应用于自动目标识别、战场监视、自动飞行器导航、机器人、遥感、医疗诊断、图像处理、模式识别和复杂工业过程控制等领域。多传感器数据融合是指对不同知识源和传感器采集的数据进行融合,以实现对观测现象更好地理解。从表面上看,多传感器融合的概念很直观,但实际上要真正实现一个多传感器融合系统是比较困难的。

近年来，多传感器信息融合实现方法有很多，成熟的多传感器信息融合方法主要有: 经典推理法、卡尔曼滤波法、贝叶斯估计法、Dempster-Shafer 证据推理法、聚类分析法、参数模板法、物理模型法、熵法、品质因数法、估计理论法和专家系统法等。用于多传感器数据融合的计算智能方法主要包括:模糊集合理论 、神经网络 、粗集理论、小波分析理论和支持向量机等。目前,人们已开始将多传感器信息融合应用于复杂工业过程控制系统。

针对多传感器问题，文献[1～4]利用模糊理论给出了融合方法，文献[5～7]利用概率模型方法进行融合；分别基于概率权、极大似然法以及贝叶斯估计等理论提出了不同的融合方法；文献[8,9]利用矩阵特征向量的稳定理论进行融合；文献[10,11]分别提出了基于支持度的融合方法和一种基于模糊贴近度函数的融合算法。本文提出了利用置信水平确定模糊隶属度，进一步构造优越性比较矩阵来进行数据的融合。

1 信息融合模

定义1[12]设在论域U上给定映射

μA︰U→[0,1],

使得x∈U→μA(x)∈[0,1],则称μA确定了论域U上一的一个模糊子集，称μA为A的隶属函数，μA(x)为x属于A的隶属度。易知，隶属度越接近1，则x属于A的可能性越大。

用多只传感器测量同一参数时，单只传感器所到的一系列数据可看成服从正态分布，或者同一时刻多只传感器测量到的一组数据可看成正态分布。

显然，可以认为越靠近期望值的数据是越接近真实值的，因此,考虑在数据融合时，离期望值越近的数据赋予较大的模糊隶属度，离期望值较远的数据赋予较小的模糊隶属度，本文利用置信度来确定模糊隶属度的值；再进一步利用特征向量函数法确定各传感器的一致性排序，根据多次测量可以给出不同的排序，取平均值后可给出不同传感器的融合权重，并可利用得到的权重方便对将来真实数据的估计。

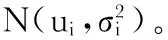
具体的数据融合过程如下：

1)参数的估计：在概率统计中，点估计是对参数值的一类估计方法，由于已知分布，在此，可采取点估计中的极大似然估计，对期望和方差的估计如下

其中，模糊集合A代表测量的值是准确的，越靠近μi的时候，其隶属度越高，越远离μi的时候，其隶属度越小。

3)传感器的一致性排序：在第i次测量中，令dj=μA(xij)，j=1,2,…,n，对多只传感器两两比较，可得优越性比较矩阵D为

求解矩阵D可得最大特征值所对应的的特征向量，由于矩阵D为非负矩阵，最大特征值对应的向量必为正向量。进一步归一化的特征向量假设为η=[η1,η2,…,ηn]T，则η中的分量表示各传感器的重要性程度,可取为相应的权重。

4)数据的融合：利用第j次测量计算得到的权重对第j(j=1,2,…,m)次的数据进行融合，得到所有传感器第j次融合的数据为

在进行m次测量后，可考虑将每次计算得到权重取平均值，令

得到各个传感器的平均权重，可将此权重作为各个传感器的权重在以后的测量中对真实数据进行估计,并可随着测量次数的增加不断改进此权重，提高估计的准确性和稳定性

2 实 验

以文献[3]中的实验来说明本文的数据融合方法。该实验采用了3只热电偶对恒温箱的温度进行测量，每只热电偶对恒温箱的温度测量了6次，得到的数据如表1。

表1 热电偶的测量值(真实值为900 ℃)

Tab 1 Measured value of thermocouple

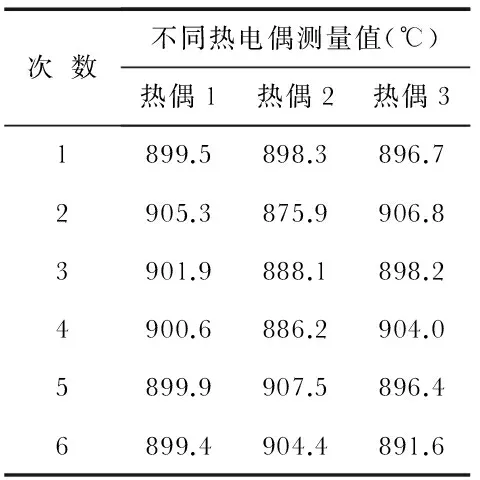
次数不同热电偶测量值(℃)热偶1热偶2热偶31899.5898.3896.72905.3875.9906.83901.9888.1898.24900.6886.2904.05899.9907.5896.46899.4904.4891.6

计算出隶属度后，可得融合后的数据，将不同方法融合的数据作比较(如表2)，包括a.平均权法，b.基于可靠性的数据融合方法，c.概率权法，d.本文方法。

表2 不同数据融合方法的比较

Tab 2 Comparison of different data fusion methods

次数不同方法融合数据(℃)abcd1898.17898.24898.17898.282896.00895.83896.24901.763896.07896.06896.17897.734896.93896.86897.06899.625897.93897.92897.80900.176898.47898.48898.41899.25

从数据的融合结果来看，基于置信权的数据融合结果大大优于其他方法。从绝对误差来作比较,如表3。

表3 不同数据融合方法误差比较

Tab 3 Comparison of errors of different data fusion methods

方法abcd误差值(℃)16.4316.6116.157.05

从表3可以明显看出：置信隶属度的方法比其它三种方法的总绝对误差要小得多，而其它三种方法的误差基本相差不大。

若将各次测量计算得到的权重取平均值，可得平均权重分别为0.4543,0.2397,0.3060。因此，第j次融合的数据为

计算可得融合数据如表4、表5(其中，e代表权重取各次测量权重的平均值)。

表4 不同方法的融合数据比较

Tab 4 Comparison of fusion data with different methods

次数不同方法融合数据(℃)abce1898.17898.24898.17898.362896.00895.83896.24898.713896.07896.06896.17897.464896.93896.86897.06898.195897.93897.92897.80900.656898.47898.48898.41898.21

表5 不同方法的总绝对误差的比较

Tab 5 Total absolute errors comparison of different methods

方法abcd误差值(℃)16.4316.6116.159.72

可以看到，取平均权重后总绝对误差增大了，但好处也是明显的，不再需要根据新测量的数据为详细比较融合效果，将实验的次数提高到200次，也就是针对3只传感器，分别随机产生服从正态分布的200个数据，再用不同方法进行数据融合，为比较的方便性，这里选用平均权法和置信隶属度法作比较。仿真的结果如图1所示。

图1 200次实验的仿真结果

可以看到，基于置信权的绝对误差要小得多，仿真结果充分说明了此方法的可靠性。

3 结 论

1)利用置信水平来确定模糊隶属度，充分考虑到了现实中此类数据服从正态分布的特点，能更好地把握数据的特点，从而得到比较好的融合数据。

2)通过构造优越性比较矩阵，不仅仅可以得到数据的融合方法，也可以通过权重看出哪些传感器的更为精确，并方便以后对真实数据的估计。

3)通过绝对误差的比较说明了此方法的有效性和实用性，通过多次仿真说明了此方法的稳定性。

[1] LeBlane Saffiotti.Multi-robot object localization：A fuzzy fusion Approach[J].IEEE Transactions on Systems，Man，and Cybemetics，Part B：Cyhemeties，2009，39(5)：1259-1276.

[2] Gao Hongyan.A simple multi-sensor data fusion algorithm based on principal component analysis[C]∥ISECS International Colloquium on Computing， Communication，Control，and Management，2009.

[3] 王婷杰 ，施惠昌.一种基于模糊理论的一致性数据融合方法[J].传感器技术，1999，18(6)：50-53.

[4] Russo F，Ramponi G.Fuzzy methods for multi-sensor data fu-sion[J].IEEE Transactions on Instrumentation and Measurement,1994，43(2)：288-294.

[5] 万树平.多传感器数据融合的概率权方法[J].传感器与微系统，2009，28(8)：12-17.

[6] 陈福增.多传感数据融合的数学方法[J].数学的实践与认 识，1995，15(2)：l1-16.

[7] 吴小俊，曹奇英，陈宝香，等.基于 Bayes估计的多传感器数据融合方法研究[J].系统工程理论与实践，2000(7)：45-48.

[8] 王 威，周军红，王润生，等.多传感器数据融合的一种方法[J].传感器技术，2003，22(9)：39-41.

[9] 涂国平.多传感器数据融合的稳健处理方法[J].数据采集与处理，1998，13(1)：85-87.

[10] 孙 勇，景 博.基于支持度的多传感器一致可靠性融合[J].传感技术学报，2005，18(3)：537-539.

[11] 杨 佳，宫峰勋. 基于贴近度的多传感器一致可靠性融合方法[J].传感技术学报，2010，23(7)：984-988.

[12] 李登峰.模糊多目标多人决策与对策[M].北京:国防科技出版社，2003.

Multi-sensor data fuzzy fusion based on confidence membership level*

HE Ming

(School of Information and Technology,Jiangxi University of Finance & Economics,Nanchang 330013,China)

In process of data fusion,take data from each sensor as normal distribution,membership degree is obtained by confidence level,construct superiority comparision matrix and then get fused data,when the method is used in evidence,and compared with the average weight,the probability weight,etc. The empirical part verify practicality of this method,and then conduct a number of simulations,by comparing absolute error,verify stability and effectiveness of this method.

multi-sensor; membership; surperiority; comparison matrix; confidence level

2015—01—22

国家自然科学基金资助项目(71461009,61263018)；江西省自然科学基金资助项目(20114BAB201012)

10.13873/J.1000—9787(2015)09—0038—03

TP 212

A

1000—9787(2015)09—0038—03

何 明(1975-)，男，江西南昌人，博士，讲师，主要研究方向为计算数学、证据理论和模糊数学问题。