对一道高考题关联的运动模型的教学思考

王 波

（南京市雨花台中学，江苏 南京 210012）

2014年全国高考第24题是一道动力学的问题.运动的特征是加速度逐渐减小为0的直线运动，这种运动规律在高中物理中很常见，涉及的知识板块较多.由于运动的非线性特征，学生在理解程度上有困难，知识迁移能力不够.笔者从这道试题出发探讨这类问题的典型特征，对这一类问题在教学上做一个总结.

高考试题.2012年10月，奥地利极限运动员菲利克斯·鲍姆加特纳乘气球升至约39km的高空后跳下，经过4min 20s到达距地面约1.5km高度处，打开降落伞并成功落地，打破了跳伞运动的多项世界纪录，取重力加速度的大小g＝10m/s2.

（1）略.

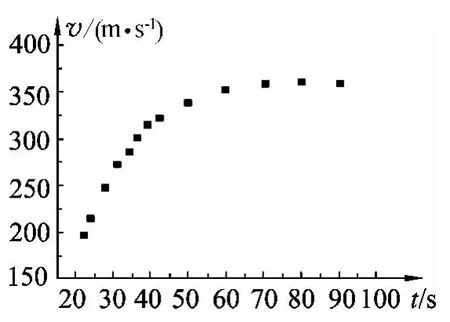
图1

（2）实际上物体在空气中运动时会受到空气阻力，高速运动受阻力大小可近似表示为f＝kv2，其中v为速率，k为阻力系数，其数值与物体的形状，横截面积及空气密度有关.已知该运动员在某段时间内高速下落的v-t图像如图1所示，着陆过程中，运动员和所携装备的总质量m＝100kg，试估算该运动员在达到最大速度时所受阻力的阻力系数（结果保留1位有效数字）.

由上题进一步延伸，可以得出这类问题的运动模型特征一般表现为：运动物体受到动力和阻力作用，其中一个为恒力（或几个恒力的合力），另一个为变力，而变力一般与速度有函数关系，所以加速度既会改变速度，又会随着速度的变化而变化，速度与时间呈现出非线性关系.运动物体的加速度逐渐减小为0，物体先做加速度减小的变速直线运动后做匀速直线运动，速度达到最大或最小.其速度图像表现为图2，图3所示.

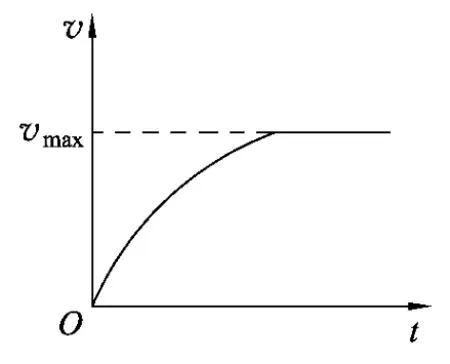
图2

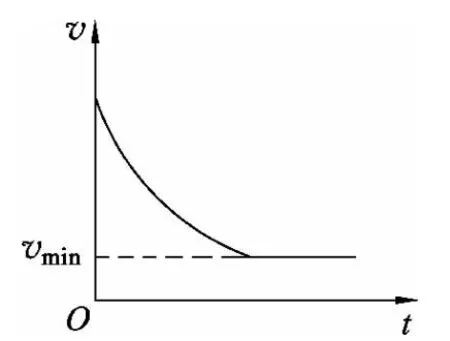
图3

“加速度逐渐减小直至为0，物体先做变加速直线运动后做匀速直线运动”这种运动模型在不同的知识模块有不同的呈现形式，下面从教学的角度举例说明.

1 动力学模块

例1.一质量为m的跳伞运动员从足够高的高空跳下，加速运动到一稳定速度v0后打开降落伞，此后受到的空气阻力与运动员速率成正比，即f＝kv，重力加速度为g.

（1）求解运动员最终的速度.

（2）设运动员从开伞到速度最小所用时间为t，求运动员从开伞到速度最小时的位移x.

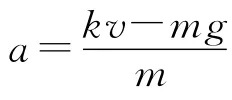
（2）由图3可知v随着t的变化是非线性的，“面积”不容易求出，高中阶段可用“微元法”解决.

取很短时间Δt，在t～t＋Δt时间内，由题意

本题中运动员受到重力（动力为恒力）和阻力（变力），初始状态决定了运动员的运动加速度与速度方向相反，随着a减小为0，速度也逐渐减小至最小值.

2 功能关系模块

例2.一辆质量为m的汽车以额定功率P从静止开始启动，汽车受到大小不变的阻力f，启动后经过时间t达到最大速度，求：

（1）汽车的最大速度；

（2）汽车达到最大速度时的位移.

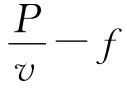
（2）汽车的运动规律如图2所示，本题涉及功率，从功能关系分析较为方便.

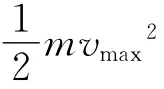
本题中汽车受到的动力（牵引力）为变力，阻力为恒力，是机车在恒定功率下运动模型的主要特点.耐心引导学生逐步分析，找到临界点，画出运动图像，结合功能关系，可以较完整地解决这类问题，也可进一步延伸，引导学生分析匀加速启动的机车运动问题.

图4

3 电磁感应模块

例3.如图4所示，相距为L的两条足够长的光滑平行金属导轨MN、PQ与水平面的夹角为θ，N、Q两点间接有阻值为R的电阻.整个装置处于磁感应强度为B的匀强磁场中，磁场方向垂直导轨平面向下.将质量为m、阻值也为R的金属杆ab垂直放在导轨上，杆ab由静止释放，下滑距离x时达到最大速度.重力加速度为g，导轨电阻不计，杆与导轨接触良好.求：

（1）杆ab下滑的最大加速度；

（2）杆ab下滑的最大速度；

（3）上述过程中，杆上产生的热量.

解析：由金属杆受力分析可知金属杆由静止开始先做加速度a减小的加速运动，当a减为0时，金属杆的速度最大，后做匀速直线运动.运动图像如图2所示.

（3）ab杆从静止开始到最大速度过程中，根据能量守恒定律有

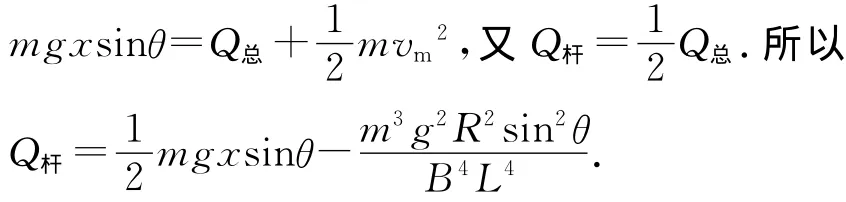
金属杆在光滑的平行金属导轨上受到的动力为重力沿导轨向下的分力mgsinθ，阻力为安培力，而安培力随速度的变化而变化.从受力特点看与前述高考题相似，从能量转化角度看与例2相似，是电磁感应中经典的单杆运动模型.

4 电磁场综合

例4.一质量为m的小滑块带正电，电荷量为q，与绝缘水平面间的动摩擦因数为μ.空间同时存在电场和磁场，匀强电场水平向右，电场强度为E；匀强磁场垂直纸面向外，磁感应强度为B，小滑块从C点由静止释放沿直线向D点运动，C、D两点间的距离为s.若小滑块运动到D点时恰好保持稳定速度继续运动，求小滑块的稳定速度大小v和此过程中摩擦力对滑块所做的功W.（滑块的带电量不变，重力加速度g.）

图5

解析：小滑块的受力分析如图，由题意可得

本题是一道较复杂的复合场问题.小滑块的运动受到电场力和摩擦力的制约，电场力作为动力是恒力，摩擦力是阻力，也是变力，其大小最终随着速度的变化而变化.由于影响因素较多，教师在引导学生在分析这类问题时要条理清晰，低起点、耐心地帮助学生理解运动规律和能量转化关系.

物体先做加速度减小的变加速直线运动后做匀速直线运动在不同知识板块表现形式不同，但分析这类问题的方法都是动力学和能量关系相结合.这类运动所蕴含的物理量之间的相互制约关系可以极好地锻炼学生分析解决问题的能力，感受物理学的魅力.