质量均匀分布天体的内部压强

许丛易

（江苏省滨海中学，江苏 滨海 224500）

1 引言

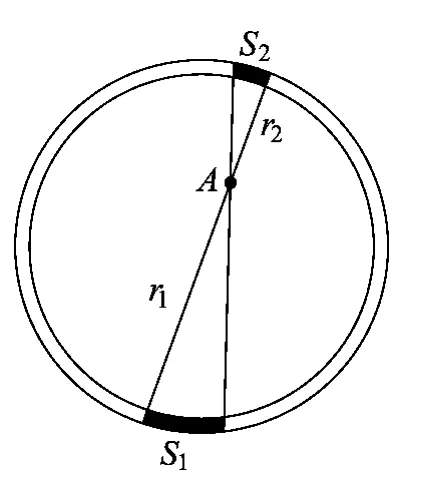
图1

在天体运动教学中，经常用到质量均匀分布的天体的一些重要结论，比如对其他天体的引力计算可以等效成质量集中在中心，质量均匀分布的球壳内部空腔任意一点引力合力为0.合力虽然为零，但是放在那里的物体会感受到向四周拉扯的引力.如图1.

过A点作两个圆锥，顶角取得极其小，它们的母线长分别为r1、r2，由于相似，它们取到的壳上的面积之比为

由（1）式知，这两个力大小相等，方向又相反，所以抵消，因此任意一块小面积引力都有对应小面积引力和它抵消，总体来说，合力为0.进而可以推广到任意厚度的壳，只要把它想象成由无数多的薄壳叠加起来的，就显而易见了.

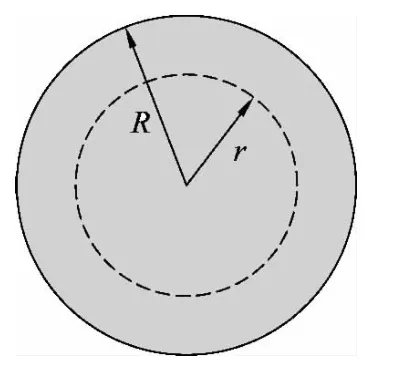
图2

例1.一星球质量为M，半径为R，求处于内部半径为r的地方重力加速度是多少？

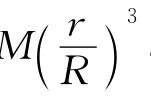
可见，内部重力加速度正比于半径，越靠近地心，加速度越小.但要注意，由于外部重力导致的压强却并不小，我们下面来求出压力随半径的表达式.

2 两种计算方案

图3

方案1：如图3求出小立体角ΔΩ对应的半径r之外的总重力，再除以立体角ΔΩ对应的半径r处的表面积即可，但是要注意，由于重力加速度不是常量了，不能用总质量直接求出来，需要积分.

可见随着r的减小，压强在增大，在中心处变成了无穷大.因为中心处面积为0，而总重力不为0，压在上面压强自然为无穷大.

再乘以面积4πx2，得

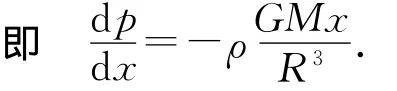
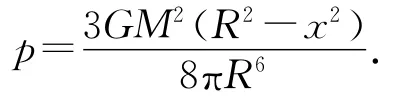
两种方案，给出了两个答案，哪一个才是合理的呢？另一个方案的问题出在哪里？

3 讨论

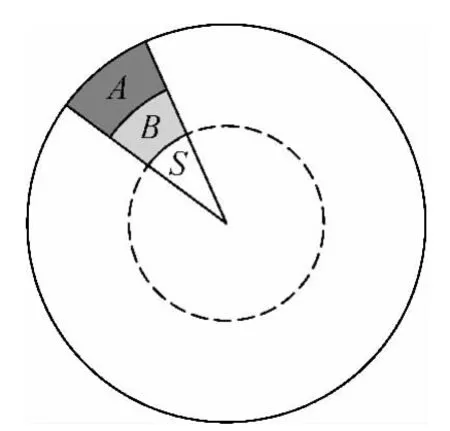
图4

我们看如图4所示的两部分，在计算重力的时候用了当地的重力加速度，而这当地的重力加速度是考虑了B对A的引力了.但是在计算它们对面积S产生的压强时，B对A的引力是它们整体的内力，不应该考虑到计算中去，方案1的模型计算了AB间的引力，所以计算结果会偏大.即

可见此题，内力只能部分地计算进去，这是一个困难的地方，不容易理解的地方，方案2的微元法没有这些困扰，是正确的.

致谢：感谢江苏省滨海中学物理组的全体成员，本论文的写作缘起于竞赛辅导课中学生的提问，当时第一感觉应该比较容易得出答案，但是结果却是错误的，于是就想专门把几种解法都剖析一下.

1 卢德馨.大学物理学（第2版）［M］.北京：高等教育出版社，2003.