无砟轨道预应力混凝土连续梁桥工后徐变变形研究

叶志荣

（同济大学建筑设计院（集团）有限公司，上海市 200092）

1 概况

目前，我国大部分高速铁路均采用无砟轨道。无砟轨道能适应高速列车高平顺性和高稳定性的要求，但可调性很小。对铺设无砟轨道的预应力混凝土连续梁桥，深入了解主梁混凝土在铺轨后的徐变变形（即工后徐变变形）具有十分重要的工程意义。目前，各种设计规范有关徐变系数计算公式的规定差别很大，由此计算得出的徐变变形值也各不相同。此外，施工过程中某些步骤的调整，如铺轨、拆除中墩墩梁临时固结的时间不同，也会对主梁的工后徐变变形产生影响。本文以宁杭客运专线某处特大桥（下称D桥）为背景，选取不同规范的徐变系数计算其工后徐变变形，比较计算结果的差异，并研究上述施工步骤的调整对工后徐变变形的影响。

D桥为70 m+125 m+70 m三跨预应力混凝土连续梁桥，全长266.5 m，为单箱单室结构，箱梁顶宽12.0 m，底宽7.0 m，中墩梁高9.2 m，端部及跨中梁高5.2 m。主梁采用C55混凝土，横纵向预应力筋采用1 860低松弛高强钢绞线。主梁采用挂篮悬臂施工，共分12个悬臂现浇施工节段。边跨采用满堂支架施工，吊篮合龙。设计荷载为ZK活载，二期恒载取值为118 kN/m。运用Midas建立梁单元有限元模型，同时模拟全桥施工过程。全桥有限元模型见图1。

图1 A桥有限元模型

2 按不同规范的徐变系数计算工后徐变变形

2.1 徐变及徐变系数定义

徐变是指在持续荷载作用下，混凝土结构的变形随时间不断增加的现象。影响混凝土徐变的因素有很多，如应力的性质和大小、加载时混凝土的龄期、荷载的持续时间、混凝土的组成材料及配合比、周围环境的温度湿度、构件的截面形式等。通常采用徐变系数φ来描述混凝土的徐变：

式中：εc——混凝土的徐变应变；

εe——混凝土的徐变应变开始时的瞬时弹性应变。

2.2 常用规范徐变系数计算方法

目前，由于各种规范的混凝土徐变系数计算公式不同，因此选用不同规范计算得出的徐变变形值差异也较大。D桥有限元模型在计算过程中分别采用了四种较常使用的规范，分别为：CEB-FIP（1978）规范、CEB-FIP（1990）规范、铁路桥涵钢筋混凝土和预应力混凝土结构设计规范（TB10002.3—2005）（下称TB05规范）和公路钢筋混凝土及预应力混凝土桥涵设计规范（JTGD62—2004）（下称JTG2004规范）。

其中，CEB-FIP（1978）规范采用的徐变系数为：

式中：φ（t,τ）——加载龄期 τ，计算龄期为t时的混凝土的徐变系数，下同；

βa——加载后最初几天产生的不可恢复的变形系数；

φd（t,τ）——可恢复的弹性变形系数，或徐弹系数；

φf（t,τ）——不可恢复的流变系数，或徐塑系数。

CEB-FIP（1990）规范考虑了混凝土的抗压强度、构件尺寸、周围环境的平均相对湿度、加载龄期等各种因素的影响，采用各种系数相乘而得到的徐变系数：

式中：φ0——名义徐变系数；

ΦRH——环境相对湿度修正系数；

Bfcm——混凝土强度修正系数；

β（τ）——加载龄期修正系数；

βc（t,τ）——徐变进程修正系数。

TB05规范采用的计算公式为：

式中：βd（t,τ）——随时间增长的滞后弹性应变；

R（τ）/R∞——混凝土龄期为 τ的强度R（τ）与最终强度R∞之比；

φf——流塑系数；

βf（t）、βf（τ）——随混凝土龄期增长的滞后塑性应变，与理论厚度有关。

JTG2004规范给出的公式只适用于强度等级为C20—C50的混凝土。采用高强混凝土时应乘以修正系数（其中，32.4为C50混凝土的轴心抗压强度标准值，fck为C50以上混凝土轴心抗压强度标准值），计算公式为：

式中：φ0——名义徐变系数；

βc（t-t0）——加载后徐变随时间发展系数。

2.3 徐变变形分析与比较

分别选用 CEB-FIP（1978）、CEB-FIP（1990），TB05和J TG2 0 0 4规范的徐变系数计算D桥有限元模型的徐变变形。提取中跨跨中处100 a内徐变变形的发展数据，绘出四种规范对应的总体徐变变形曲线（见图2）；将图2曲线中各时间点处的徐变变形值减去铺轨前的初始徐变变形值，得到中跨跨中处的工后徐变变形值，并绘出曲线（见图3）。图中，纵坐标正值表示变形上拱，负值表示变形下挠。

图2 中跨跨中合计徐变变形曲线

图3 中跨跨中工后徐变变形曲线

由图2可以看出，按TB05规范计算的总体徐变变形最大，变形值在轨道铺设后为15.5 mm，100 a后可达33.1 mm。发展速度上，TB05规范的曲线在最初的6 a里增速最快，第6年总体徐变变形为24.2 mm，相比铺轨初期增长了8.7 mm。TB05规范的计算结果表明，在最初的6 a里工后徐变变形就已达到100 a工后徐变变形的5 0%。6 a后曲线虽仍呈上升趋势，但增速明显减小，直至与时间轴趋于平行。

JTG2004规范对应的变形曲线与TB0 5规范的曲线形状相似，但数值偏小。同样，若选用JTG2004规范规定的徐变系数，最初6 a里，合计徐变变形从开始的11.3 mm迅速发展至16.8 mm，工后徐变值约占100年工后徐变总值的65%。

与我国规范不同的是，CEB-FIP（1978）和CEB-FIP（1990）规范的计算结果无论是合计变形还是工后变形都是随时间发展而下降的，工后徐变表现为随时间下挠。参照我国已建成的同类型桥梁的10 a徐变实测数据，预应力混凝土连续梁桥跨中工后徐变变形基本都是随时间增长而逐渐上拱的。由此可见，采用CEB-FIP规范的徐变系数时计算结果与实际情况存在较大不同，而采用我国两种规范定义的徐变系数时计算结果切合实际。根据规范要求，对于跨度大于50 m的高速铁路梁桥，工后徐变上拱值不得超过l/5 000且不大于20 mm，由TB05和JTG2004规范计算得出的工后徐变变形值均满足要求。

3 铺设轨道的时间对工后徐变变形的影响

施工中降低主梁混凝土工后徐变主要有三种控制方法：延迟铺轨、张拉体内预应力束、张拉体外预应力束。后两种方法工序繁琐，不常采用，因此确定轨道铺设的时间对混凝土主梁的工后徐变显得尤为重要。

以D桥有限元模型为基础，考虑9种假定的延迟铺轨的工况，将铺轨时间依次设为全桥合龙完成后的 0 d、60 d、120 d、180 d、1 a、2 a、3 a、5 a、10 a。分别采用TB05规范和JTG2004规范的徐变系数进行计算，绘出跨中点在中跨预应力张拉完成3 a后的工后徐变变形曲线，见图4。

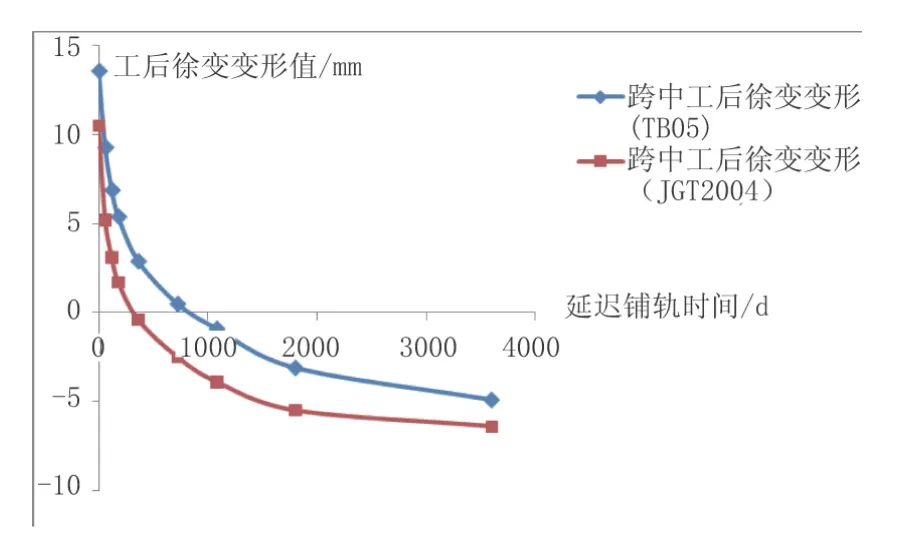
图4 连续梁跨中工后徐变变形与延迟铺轨时间的关系曲线

可以看到，根据两种规范计算结果绘出的曲线变化规律基本类似，即随着铺轨时间的延迟，跨中点处的工后徐变变形逐渐从上拱转为下挠。取TB05规范的计算数据分析，若在中跨合龙完成后立即铺轨（0 d），对应的工后徐变变形为13.6 mm；在两个月后铺轨（60 d），工后徐变变形值为9.3 mm，相比0 d时上拱度减少了31.6%；在半年后铺轨（180 d），跨中工后徐变变形值为5.4 mm，相比0 d上拱度减少达60.2%之多。。可见，延迟铺轨能极为有效地解决连续梁工后徐变变形上拱度过大的问题。考虑施工工期等各方面要求，一般选在中跨合龙60 d后进行铺轨。

4 拆除中墩临时固结时间对变形曲线的影响

一般情况下，悬臂施工中应在0#块设置墩梁临时固结，以使0#块梁段能够承受两侧悬臂施工产生的不平衡弯矩。在对悬臂现浇结束之后，何时拆除临时固结是一个值得关注的问题。

我国目前的悬臂施工方法中，拆除中墩墩梁临时固结的时间选择主要有两种，一是在边跨合龙完成后拆除墩梁临时固结，二是在中跨合龙完成后拆除墩梁临时固结。对这两种做法优劣的判断主要从主梁变形和应力包络图等方面来予以考虑。

以TB05规范为计算依据，利用Mi d a s模拟两类拆除墩梁临时固结的工况进行对比。通过观察施工阶段的应力包络图，发现两种工况下的梁体应力性质大致相同，主梁截面在施工阶段的整个过程中均可保证全截面受压，在容许应力法下主梁压应力小于容许应力，满足相关要求。

在边跨合龙完成后拆除中墩墩梁临时固结工况下，轨道铺设完成后和轨道铺设完成3 a后这两个时间点上的梁体合计变形分别为-15.8 mm和-12.3 mm，工后徐变变形为3.5 mm；在中跨合龙完成后拆除中墩墩梁临时固结工况下，对应于同样两个时间点上的的主梁合计变形分别为-8.8 mm和-5.4 mm，工后徐变变形为3.4 mm。

由此可见，无论是在边跨合龙完成后拆除中墩墩梁临时固结，还是在中跨合龙完成后拆除临时固结，连续梁主梁的工后徐变变形差别不大。但中跨合龙后拆除中墩临时固结相比边跨拆除需设置的预拱度较小，且可以不设临时纵向支座，更便于施工。

5 结论

（1）按照不同的规范计算预应力混凝土连续梁桥的工后徐变变形有较大的差异。我国目前常用的两种规范中，TB05规范的计算结果大于JTG2004规范的计算结果。

（2）连续梁工后徐变变形在轨道铺设后初期发展最快，轨道铺设完成后1～6 a内的工后徐变可达到100 a工后徐变变形的40%～60%。

（3）工后徐变变形在各规范下计算结果的差异主要由各规范的徐变系数计算公式不同引起。

（4）延迟轨道铺设的时间能有效降低连续梁工后徐变变形的上拱度。

（5）悬臂施工过程中，边跨合龙后拆除中墩临时固结和中跨合龙后拆除临时固结对主梁截面的应力状态和工后徐变影响不大。

[1]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.

[2]何义斌.大跨度无砟轨道连续梁桥后期徐变变形研究[J].铁道学报,2008,30(4):120-124.

[3]陈守辉.大跨度预应力混凝土连续箱梁桥收缩徐变效应分析[J].铁道建筑技术,2009(8):15-17.

[4]叶梅新,钱淼,刘杰.无碴轨道预应力混凝土桥梁徐变变形控制方法研究[J].铁道标准设计,2009(2):92-94.

[5]崔幼飞.大跨度无碴轨道混凝土连续梁桥的施工计算及徐变变形研究[J].石家庄铁道学院学报,2008(3):62-65.