基于曲线投影模型的电子断层三维重构并行算法

张静蓉万晓华张 法

1(中国科学院计算技术研究所 北京 100190)

2(中国科学院大学 北京 100049)

基于曲线投影模型的电子断层三维重构并行算法

张静蓉1,2万晓华1张 法1

1(中国科学院计算技术研究所 北京 100190)

2(中国科学院大学 北京 100049)

大尺度高精度的电子断层三维重构可以获得在更大视角下的生物大分子三维结构的细节信息。但研究尺度的增大给获取高精度重构结果和缩短数据处理时间带来了巨大的挑战。TxBR 提出的曲线模型显著提高了重构的精度，但其计算比直线模型更复杂耗时，且在曲线模型下，之前的并行策略不再可行。针对这一问题，提出了一种在 GPU 平台上实现的针对曲线模型的分块迭代并行算法。通过对曲线模型的研究发现，曲线模型具有一定的空间局域性，利用这种性质提出了一种纵向的分块方式。在算法的实现阶段，提出一个基于页的数据传输策略，从而能够去除冗余的数据传输，减少数据传输带来的时间消耗。实验结果显示，本算法可接近 40 倍的加速比。

电子断层；迭代重构算法；分块；曲线投影模型；GPU 并行

1 引 言

电子断层三维重构(Electron Tomography， ET)是利用生物样品的电子显微投影图像重构出生物体三维结构的技术。其主要策略是将制备好的生物样品放在透射电子显微镜中，让样品沿着一个与电子束垂直的轴旋转，每旋转到一定角度，拍摄得到样品的一张二维投影图片[1]。然后对这一系列二维投影图像进行对位，利用三维重构算法得到样品的三维结构。由于透射显微镜的物理限制，样品的旋转角度范围在(－60°，＋60°)或(－70°，＋70°)之间，同时由于样品可以承受的电子剂量有限，投影图像往往噪声很大。与直接重构算法相比，迭代重构算法可以更好地处理ET 中有信息缺失和高噪声的图像。

随着投影图像尺度的增大，大尺度高精度的电子断层三维重构研究越来越受到关注。目前大多数的重构算法都采用直线投影模型。然而受到磁场的影响，电子束的轨迹是曲线，所以直线投影模型并不准确，由此产生的误差会随着投影图像尺度的增加变得更加明显。为了减少这一误差，研究人员提出了一种全局的非线性投影模型—TxBR[2]。与直线模型相比，这一模型可以提高重构的精度，但其计算更加复杂耗时。

在大尺度高精度的电子断层重构中，我们常常使用高性能计算来帮助解决计算量大，耗时长的问题。GPU(Graphics Processing Units)由于其出色的加速效果和较低的硬件成本常常被大家采纳。目前已有许多 GPU 加速的框架。TxBR 也采用了一种并行策略为曲线模型下的直接重构算法进行加速[3]。在此并行策略中，三维的重构数据沿着z轴被分割为几个部分(z-section)。每一个z-section 会被单独地传输入 GPU 进行重构。然而这一并行策略并不适用于迭代算法的重构。因为在每一轮迭代，算法都需要将所有z-section 在GPU 与 CPU 传输一次。对于 GPU 来说，这样的数据传输十分耗时。目前的投影图像的大小已经达到了 8192×8192 像素，甚至更大[3,4]，相应的重构结果会达到几个 GByte[5]。由于 GPU 的显存有限，这将进一步使 GPU 并行变得困难。

针对这一问题，我们提出了一种改进的分块迭代重构算法，并且在 GPU 平台上实现了算法的并行。我们的贡献主要在两个方面：首先，分析了曲线投影模型的局部性特征，并根据此特征将数据纵向划分，从而提出了一种新的分块迭代重构算法；其次，针对大规模 ET 重构数据，提出了一种基于页的 GPU 数据传输策略，以减少数据传输时间，提高并行效率。

2 相关研究

2.1 迭代重构算法

电子断层重构通过透射投影图像获得样品内部结构。在实域空间中，迭代算法通过将此问题形式化为线性方程组求解问题。以“立体像素”为最小的三维空间的单位，我们可以将三维重构结果表示为N个立体像素点(N＝nwidth×nlength×nheight，nlength、nwidth和nheight分别是样品的长、宽和高)。同时假设二维投影像素点的数目为M(M＝npro_width×npro_length×nang，其中npro_length、npro_width和nang分别是投影序列的长、宽和角度数)。投影的过程可以用公式(1)来表示：

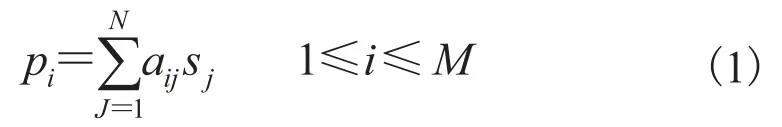
其中，pi是第i个像素点的值；sj是第j个立体像素点的值。在矩阵A中，aij表示第j个立体像素点对第i个二维投影像素点的贡献。矩阵A中各元素的值是由投影模型来决定的。 我们通过迭代算法来求解向量的值。

迭代重构算法大致可分为顺序迭代算法、分块迭代算法和同步迭代算法三大类[6]。在本质上，顺序迭代算法和同步迭代算法都是分块迭代算法的特殊情况[7]。假设将所有线性方程组中的方程分为B组，每组方程的数目为T。我们可以获得一种通用的迭代重构算法公式：其中，b＝kmodB是分块的序号；i是方程在线性方程组中的编号； 是权重因子。松弛因子λk子对于迭代算法的收敛速度有较大的影响[8]。

对于顺序迭代算法(B＝M，T＝1)，每次更新数据只考虑使用一个约束。同步迭代算法(B＝1)每次更新需要考虑方程组中的所有约束，例如经典的同步迭代算法 SIRT[9](Simultaneous Iterative Reconstruction Technique)。分块迭代算法每次更新数据的时候只考虑一组方程，一轮迭代会更新数据B次。传统的分块迭代算法如BICAV[10]和 ASART[11]，都是采取逐角度更新的，每一个分块中方程的数目为T＝npro_width×npro_length，分块的数目为B＝nang。

2.2 曲线投影模型

在投影数据获取的过程中，有很多因素会影响重构结果的精度。首先，由于地球磁场的影响，电子的运动轨迹是曲线而不是通常认为的直线；其次，在电子光学设备中，球面像差很明显，使得投影中较小的细节模糊不清；再次，样品在旋转的过程中，不同部分在磁场的位置不同，这会导致样品各部分成像的放大倍数不一致。同时样品的扭曲与损失也会使重构的结果变差。

面对上述这些问题，为了获得较好的重构结果，TxBR[2]使用了一种捆绑调整算法求得一种非线性的投影模型。在本文中我们采用二次的曲线投影模型来描述投影图像与三维样品之间的非线性变换关系，公式如下：

该公式描述了三维数据到二维投影图像的映射关系。(X,Y, Z)是立体像素的坐标，其在角度下θ下对应的投影坐标是(x,y)。此公式中的系数都是由捆绑调整算法计算得到的，其细节在Lawrence 等[2]的研究中有详细论述。

2.3 并行迭代算法

由于 GPU 的内存有限，对于大尺度的电子断层重构问题，我们无法将所有的数据直接放入 GPU中，因此需要考虑如何完成数据的分割。

线性投影模型(如图 1(a)所示)假设电子束沿着直线传播，所以电子轨迹是彼此平行的。在线性投影模型前提下，样品中垂直于旋转轴的一个切片总是被认为会投影到一条直线上，从而三维重构问题可以分解为多个二维重构问题。使用前面所描述的算法，二维重构问题可以利用对应的一维投影图像求解。目前大多数的并行重构算法都是采用这样的策略[12-14]。但是这一策略并不适用于曲线投影模型，因为在曲线投影模型(如图1(b)所示)下，我们认为电子束的运动轨迹是曲线，彼此之间并不平行，所以三维重构问题不能简单地分解为多个二维重构问题。

图 1 直线投影模型与曲线投影模型Fig. 1 Straight-line model and curvilinear model

TxBR 提出了一种在曲线模型下针对直接重构算法的 GPU 并行策略[3]。该策略将三维数据沿着z轴分割为几个部分，每次独立的重构其中一个部分。然而这一并行策略需要大量的数据重复传输，并不适用于迭代重构算法。到目前为止，还没有针对曲线模型下迭代重构算法的 GPU 并行策略。

3 技术细节

如前所述，针对曲线投影模型，目前没有相关的 GPU 并行迭代重构算法。相对于大尺度的重构数据来说，GPU 的内存十分有限，所以找到一种适合的数据划分策略是解决迭代重构算法GPU 高效并行的关键问题。为了解决这个问题，我们首先研究了曲线模型的特点，并据此提出了一种数据分割的策略，之后相应地修改了传统的SIRT 迭代重构算法。最后为了更加有效地减少数据传输的消耗，提出了一种基于页策略的 GPU数据传输方式。

3.1 曲线投影模型的局部性

在直线投影模型下，我们认为电子束的运动轨迹是直线，它们的轨迹是互相平行的，切片的投影始终是一条直线。但由于受到地球磁场等的影响，一个纵向切片的投影实际上是一条曲线。反过来看，投影到同一条直线上的立体像素点实际上是位于一个曲面上的。这个曲面会横跨很多个纵向切片(如图 1(b)所示)，而且曲面的形状会随着样品旋转角度的变化而变化。但是这个曲面是具有一定局部特性的。直观地讲，假设旋转轴是y轴，y轴坐标值小的投影点对应的立体像素点的Y值也不会很大。

将公式(3)和(4)的左边的值x和y固定，则这两个式子描述了一条二次的三维空间曲线；如果只是固定x值(x＝c)，则式子(3)描述的是一个三维空间中的曲面(如图 1(b)中展示的曲面)。根据此表达式，我们可以进一步利用数学中关于曲面极值的相关知识来定量研究曲面的局部性。

将方程(3)看作一个隐函数，其中X是因变量而Y和Z是自变量。要定量地研究曲面的局部性，首先要将该问题形式化地表示，即在一个有限的范围内求解曲面的极值点。该有限的范围是样品的空间范围。基于所讨论的具体问题，这个曲面是一个连续的曲面，其局部最大值和局部最小值可能是曲面的极值点，也可能是在边缘曲线上。因此首先要求解曲面在给定范围内的极值点，再分析边缘曲线的极值。这些点中的最大值和最小值就是我们需要的结果。

对于多元可微分函数，极值点首先是偏导数等于零的点，所以我们需要加入对于偏导数为零的约束条件，得到的方程如下：

接下来考虑边缘数据的局部最大值和最小值，空间曲面与样品边界相交会出现这些边界线。很明显曲面一定会和样品的上下两个面相交，但并不会与样品的所有面相交，随着角度的变化，不同的曲面与样品的交界并不一定相同。考虑所有情况，如求解曲面与平面Z＝Zmax交线的极值点需要用到公式：

边界曲线的端点也可能是极值点，例如：

通过这几步，我们可以获得某一个曲面的局部最大值和最小值，亦即可得到投影点对应的空间三维点所在的范围。假设结果是，则显然该结果会随着角度的变化而变化，也会随着c值的变化而变化。

3.2 纵向分块迭代重构算法

与同步迭代算法重构不同，分块迭代重构算法每次更新数据只需要一部分约束条件，整个迭代过程是通过每次选取不同的约束方程子集来进行的。目前将约束方程分块的方法是基于角度的，例如 SIRT 是按照投影点的顺序将对应方程分块。每一个块的大小相同，是一个角度下所有投影点对应的方程，块的数目与投影角度数一致。

如前所述，由于 GPU 的内存有限，所以对于大尺度三维重构，需要考虑如何完成数据的分割。在直线模型下，三维重构问题可以分解为多个二维重构问题。这样的数据分割不会引入多余的通信消耗。但是在曲线投影模型下，每次迭代都需要将所有的数据传入 GPU 并对其进行更新，这对于全局内存小于重构数据的情况就意味着，需要在一次迭代过程中将所有的数据分批次地在 GPU 与内存之间传输，这将导致计算性能的急剧下降。在之前直线投影模型分割方式的启发下，我们提出了一种新的基于 GPU 的分块迭代重构并行算法，将三维重构结果利用曲线投影模型的局部性分割为横跨几个切片的纵向切块，同时利用分块迭代重构算法每次只更新需要约束方程子集特点的数据。

首先将投影图像序列垂直于旋转轴均匀地分割为B个部分。对于给定的分割数目B＝b，利用曲线投影模型的局部性可以估计出每个部分的投影点集合St：

其次，利用曲线投影模型的空间局部性，可以根据投影点的范围计算得到对应三维空间点的范围，再利用坐标信息通过代码完成数据分割。这些投影点方程中的非零点(X,Y,Z)一定在此范围内。根据求出的X的范围，可将三维重构数据分割为几个纵向的切块。每次更新数据，只需要将一个切块传输入 GPU 就可以。这样极大地减少了数据传输对于 GPU 并行的影响。

图 2 改进的分块迭代重构算法Fig. 2 Modified block iterative method

综上所述，首先对所有投影点(x,y,g)进行整体分割，运用之前所述的曲面求极值的方法求出它们所对应的所有三维空间点的范围。接着按照这一计算结果，对三维空间点(X,Y,Z)进行纵向的分割，如图 2 所示，每次更新过程中，只将一部分投影点和它对应的三维空间点传入 GPU 以完成算法的更新。在一次迭代结束之后，再将下一块数据放入 GPU。

其中，分割的数目B受限于 GPU 全局内存的大小，用sizeslab表示最大的纵向切块需要的内存大小，sizepro表示投影图像的大小，sizeinter表示其他中间变量占的内存大小。同一时刻需要的内存大小可以表示为：

3.3 基于页的数据传输策略

由于相邻的纵向切块之间有重复的部分，如果每次重构一个纵向切块后就将其传输出去，重复的数据会被重复传输。我们提出了一种基于分页的数据传输策略消除冗余的数据传输。在该策略下，相邻纵向切块之间的重叠数据不会在前一个切块重构之后传输回 CPU，而是留在 GPU 中等待第二个纵向切块的其他数据传入后，一起完成第二个纵向切块的重构。这样，每次只将不再需要的数据传输回 CPU。

这种策略的最基本思想是延迟拷贝，只有不需要的数据才会传输出去。但是如果每次只将不用的数据传输，然后将有用的数据传入 GPU，将会导致传出的数据比新传入的数据量小，使得传入的数据没有足够的空间进行存储。借鉴内存管理的思想，我们将 GPU 的全局内存分割成相同大小的页，并使其作为每次数据传输的基本单位。以实际数据为例，使用投影大小为 512×512的数据，则整个投影图像的序列有 121 张。其重构的结构的尺寸是 650×683×101，空间坐标分布为{(X,Y,Z)|X∈[－87, 563],Y∈[－31, 652],Z∈[－62, 39]}。将投影图像沿着垂直于旋转轴的方向，把投影图像分给为 8 份，对应的样品空间点也会沿着垂直于旋转轴的方向分割为 8份，其对应的纵向切块的分布如表 1。

表 1 中，“Slab”表示切块的序号；“Start”和“End”分别对应于每一个分块的起始位置和终止位置的X值；“Out”对应的数据是在将本分块更新完成后需要传出数据的大小，它是以X值所涉及的范围表示的，比如第一个分块在迭代完后，需要传出的实际数据量是(－12－(－78)＋1)×683×101＝67×683×101；“In”和“Range”都是直接用X的范围来表示数据量的大小，其中“In”表示了本分块在迭代开始之前需要传输进去的数据量大小；“Range”表示的是一个分块所涉及的数据量的大小。

由表 1 可看出，相邻分块之间重叠的部分达到了整个分块的 3/4，所以去除冗余的数据传输很有必要。此外，每次传入和传出的数据量相差不大，这就保证了该策略可以有效地利用全局内存。

表 1 纵向分块的情况Table 1 The distribution of slabs

对数据按照传输的过程重新进行分割，数据自动分页的算法如下：首先，以每个块的开始位置作为页的起始处，保证每次传输出去的数据都是下一次迭代中不需要的。在保证页的起始位置正确的前提下，尽可能多地传入数据以达到充分利用全局内存的作用。

这里的旋转轴是x轴，将生物样品的三维密度点按照求出的X值进行分割，得到的数据分布如表 2。

表 2 数据的页分布Table 2 The distribution of pages

在每一轮迭代的开始，都先将第一次更新需要的数据(Page 1 to 5)全部传入 GPU。在接下来的分块迭代中，将不再需要的一页数据(Page 1)传出，并将新的一页数据(Page 6)传入。在样品的最后一页数据(Page 10)传入 GPU 的同时停止数据的传入和传出。在本轮的迭代结束以后，可以开始新的一轮的迭代。

4 实 验

在实验部分，我们首先对分块迭代的 SIRT算法与同步迭代的 SIRT 算法的重构结果进行了比较；其次，讨论了并行算法的时间消耗。

本实验使用的生物样品厚度为 350 nm，使用放大倍数为 37 K 的 300 kV FEI Titan TEM透射显微镜拍摄透射投影图像，投影图像序列有 121 张，角度范围为(－60°，＋60°)，投影图像的大小为 512×512。重构结果的大小为651×684×101。实验中的数据分割方法在“基于页的数据传输策略”中已讨论。

所有实验均在 64 位 Ubuntu12.04 操作系统上实现，使用的 GPU 显卡是 NVIDIA GTX480，具有 480 SPs 和 1536 M 全局内存。

4.1 重构结果

所有实验均采用二次曲线投影模型。在本实验中，我们考虑了三种情况：(1)使用传统的同步迭代重构算法 SIRT；(2)将数据分割为 4 个切块，使用分块迭代版本的 SIRT 算法更新数据；(3)将数据分割为 8 个切块，使用分块迭代版本的 SIRT 算法更新数据。当分块的数目为 1 时，分块迭代重构算法就变成了同步迭代重构算法。实验中主要考虑两个参数：松弛因子和迭代次数。这里将所有投影点对应的方程都定义为一轮迭代。因为当松弛因子 0＜λ＜2 时，SIRT 算法保证收敛[15]，本实验中松弛因子λ分别取值为1、0.5、0.2 和 0.1。

在本实验中，我们使用投影误差作为评判结果好坏的标准。投影误差反应了再投影与原始投影图像之间的误差。这里使用绝对平均误差(MAE)作为投影误差的依据。

图 3 绝对平均误差Fig. 3 Mean absolute projection error

其中，pi是实验获取的投影原始图像；是利用重构结果求出的再投影结果。图 3 中的曲线显示了绝对平均误差的结果。可以看出，对于不同的松弛因子，分块迭代算法都比同步迭代算法在前20 轮收敛的速度更快。这说明分块迭代算法的收敛速度更快。将数据分割为 8 个切块的分块迭代算法比分为 4 块的分块迭代算法的投影误差更小，结果精度更高。通过松弛因子λ的不同取值可以发现，本测试数据，比较大的松弛因子可以获得更好的重构结果。

图 4 展示了 50 轮迭代之后同步迭代算法与分块迭代算法的重构结果。图 4(a)为同步迭代算法 SIRT 的重构结果，图 4(b)是分块迭代版本的SIRT 算法的重构结果。两者的结果差距不大，但同步迭代算法在一些细节上更加清晰。

图 4 重构结果Fig. 4 Reconstruction result

4.2 并行算法的效果

我们在 GTX480 上测试了分块迭代重构算法的运行时间。具体的运行时间和加速比如表 3 所示。表 3 中，B表示分块的数目(B＝4 表示将所有投影点分为 4 组，相应地，三维结果被分为了4 个纵向切块)。

可以看到运行时间基本与迭代的次数成正比。总体来说，分块数目为 4 的迭代算法的运行时间少于分块为 8 的迭代算法的运行时间。这是因为分块数目越多，并行处理的数据越少，算法的并行度会降低。所以在硬件允许的前提下，应该尽量减少分块的数量。

表 3 算法执行时间与加速比Table 3 Running time and speedup

5 结论与讨论

曲线投影模型能够提高大尺度电子断层重构的精度，但它的计算复杂高，限制了曲线投影模型的广泛应用。在电子断层三维重构领域，有许多关于三维重构算法的并行加速工作。绝大部分的工作是在直线模型下对迭代重构算法采用 MPI或 GPU 并行。 目前针对曲线投影模型的工作并不多。已有的并行加速工作主要是针对直接背投影算法。我们采用 GPU 对于更加耗时的迭代重构算法进行加速， 使得在曲线模型下的迭代算法也可以快速地获得结果。

本文提出了曲线模型下，针对迭代重构算法的 GPU 并行算法。在我们的工作中，我们通过对曲线模型的研究发现曲线模型具有一定的空间局域性，利用这种性质我们提出了一种纵向的分块方式。在算法的实现阶段，我们提出一个基于页的数据传输策略，从而能够去除冗余的数据传输。实验结果显示，本算法可以接近 40 倍的加速比。在以后的工作中，我们会将本文提出的并行策略应用到其他的并行平台上，并采用更多的实验数据来验证我们的算法。

[1] Phan S, Lawrence A, Molina T，et al. Txbr montage reconstruction for large field electron tomography [J]. Journal of Structural Biology, 2012, 180: 154-164.

[2] Lawrence A, Bouwer JC, Perkins G, et al. Transform-based backprojection for volume reconstruction of large format electron microscope tilt series [J]. Journal of Structural Biology, 2006, 154(2): 144-167.

[3] Lawrence A, Phan S, Singh R. Parallel processing and large-field electron microscope tomography [C] // World Congress on Computer Science and Information Engineering, 2009: 339-343.

[4] Wan X, Phan S, Lawrence A, et al. Iterative methods in large field electron microscope tomography [J]. SIAM Journal on Scientific Computing, 2013, 35(5): S402-S419.

[5] Agulleiro JI, Fernández JJ. Evaluation of a multicore optimized implementation for tomographic reconstruction [J]. PloS One, 2012, 7(11): e48261.

[6] Censor Y. Parallel optimization: theory, algorithms and applications [D]. Oxford: Oxford University Press, 1997: 127-190.

[7] Aharoni R, Censor Y. Block-iterative projection methods for parallel computation of solutions to convex feasibility problems [J]. Linear Algebra and Its Applications, 1989, 120: 165-175.

[8] Herman GT, Meyer LB. Algebraic reconstruction techniques can be made computationally efficient [J]. IEEE Transactions on Medical Imaging, 1993, 12(3): 600-609.

[9] Gilbert P. Iterative methods for the threedimensional reconstruction of an object from projections [J]. Journal of Theoretical Biology, 1972, 36(1): 105-117.

[10] Censor Y, Gordon D, Gordon R. BICAV: A blockiterative parallel algorithm for sparse systems with pixel-related weighting [J]. IEEE Transactions on Medical Imaging, 2001, 20(10): 1050-1060.

[11] Wan X, Zhang F, Chu Q, et al. Three dimensional reconstruction using an adaptive simultaneous algebraic reconstruction technique in electron tomography [J]. Journal of Structural Biology, 2011, 175(3): 277-287.

[12] Wan X, Zhang F, Chu Q, et al. High-performance blob-based iterative reconstruction of electron tomography on multi-gpus [C] // Bioinformatics Research and Applications, the 7th International Symposiu, ISBRA 2011, 2011: 61-72.

[13] Fernández JJ. High performance computing in structural determination by electron cryomicroscopy [J]. Journal of Structural Biology, 2008, 164(1): 1-6.

[14] Castaño Díez D, Mueller H, Frangakis AS. Implementation and performance evaluation of reconstruction algorithms on graphics processors [J]. Journal of Structural Biology, 2007, 157(1): 288-295.

[15] van der Sluis A, van der Vorst HA. SIRT-and CG-type methods for the iterative solution of sparse linear least-squares problems [J]. Linear Algebra and its Applications, 1990, 130: 257-303.

A Parallel Reconstruction Algorithm Based on Curvilinear Projection Model in Tomography

ZHANG Jingrong1,2WAN Xiaohua1ZHANG Fa1

1(Institute of Computing Technology,Chinese Academy of Sciences,Beijing100190,China)
2(University of Chinese Academy of Sciences,Beijing100049,China)

Large-field high-resolution electron tomography enables visualizing detailed mechanisms under global structure. As field enlarges, the distortions of reconstruction and processing time become more critical. TxBR has proposed a curvilinear projection model, which can dramatically improve the quality of reconstruction. But its computation is more complex and time-consuming. Furthermore, previous parallel strategies are not suitable for curvilinear projection model. In this work, a block iterative parallel algorithm using curvilinear projection model on GPU platform was proposed. By studying the locality of curvilinear projection model, we proposed a vertical data decomposition method. We also adopt a page-based data transfer scheme to reduce the processing time. Experimental results show that our method can yield speedups of approximate 40 times.

electron tomography; iterative reconstruction methods; block; curvilinear projection model; GPU parallel

Q 617

A

2014-01-15

：2015-03-17

张静蓉，博士研究生，研究方向为生物信息与 GPU 并行；万晓华，博士，助理研究员，研究方向为生物信息、生物医学图像处理与高性能计算；张法(通讯作者)，博士，副研究员，研究方向为生物信息与 GPU 并行，E-mail：zhangfa@ict.ac.cn。