三维点云中的二维标记检测

林文珍 黄 惠

(中国科学院深圳先进技术研究院 深圳 518055)

三维点云中的二维标记检测

林文珍 黄 惠

(中国科学院深圳先进技术研究院 深圳 518055)

特征检测在物体识别、数据配准等应用中具有至关重要的作用。同一场景中不同采集数据的配准和融合，必须已知或者估算不同数据中的共同特征对应点。然而，许多场景缺少有效对应特征点。解决该问题的一种有效的方法是在场景中添加标记以增加特征。文章提出一种在只含有位置信息的三维点云中自动检测二维标记的方法。该方法首先在三维场景添加黑色圆形薄纸片作为二维标记，利用区域增长法将获取的三维场景的点云数据分割成不同类别，然后基于随机抽样一致性算法的扩展方法依次对分割后的点云进行形状拟合，最后通过检测形状检测该二维标记。该方法能够有效地检测出三维场景中的二维标记，并避免了遮挡、形变等问题，为缺少特征的场景提供了简单可行的特征，可广泛应用于数据配准、物体识别、物体追踪、三维重建等领域。

点云分割；随机抽样一致性；拟合；二维形状检测

1 引 言

1.1 特征检测背景

特征检测在计算机图形图像领域有着至关重要的地位，广泛应用于图像配准、物体识别、物体跟踪等领域。一般来说，特征点需具备以下属性[1]：

(1)再现性：物体相同部位的特征点能够在不同的观察条件下被检测出，例如物体的平面旋转；

(2)独特性：检测出的特征点能够很好地区分不同的物体；

(3)局部性：特征应该是局部的，以降低闭塞的概率，并允许不同观察条件下得到的不同数据之间的几何变形的简单模型估计；

(4)数量大：特征点的数量应该足够大，能提供足够的被检测物信息用于匹配或者识别；

(5)准确性：检测出的特征点应该能够准确地体现出被检测物的形状，以及物体在场景中的位置等信息；

(6)有效性：针对实时应用，特征点检测算法应该能够在有效的时间范围内进行。

现阶段大多数特征检测算法难以同时满足上述条件，使得后续的物体配准和识别的难度增大。例如，欲进行数据采集的场景的面积远远超出采集设备的视角；或者薄板(如桌面)的上下两面并没有有效的重叠部分，难以配准。

虽然研究者已经提出许多针对特定应用场景的解决方案，但是，由于存在场景特征检测难和场景本身缺少特征[1]等问题，特征检测依然面临很大的挑战。Martin[2]指出，利用人工设置简单标记可以有效解决此类问题。

人工标记一般可以分成两类：(1)在已获取的数据中手动标定出特征。用这种方式标记出的特征，其正确率往往受主观因素影响，并且随着数据数量增加，人工工作量也会大幅度增加。(2)在真实场景中添加二维或三维物体作为标记[2]。由于可以大幅度减少人工工作量，并且能够直接在三维空间中进行操作，这种方法得到了快速的发展。然而，这类方法比较依赖于标记的检测过程，如果检测失败，则可能使得后续的工作无效。

在真实场景中放置的标记可以是三维或二维物体。其中，三维标记由于易造成对场景本身信息的遮挡，产生较大的数据缺失。相比之下，二维标记的特性稳定，对场景本身的影响较小。但是，二维标记的设计和检测比三维标记困难，因为在三维空间中的二维物体是平面的，在采集数据中易被忽略，使得其几何特征难以检测[3]。

本文提出一种在三维点云中自动检测二维标记的方法。首先，在三维场景添加二维标记，利用区域生长法将获取的三维场景的点云数据分割成不同类别；然后，基于随机抽样一致性(Random Sample Consensus，RANSAC)的扩展方法依次对分割后的点云进行形状拟合；最后，通过检测形状检测该二维标记。

1.2 二维标记检测的相关工作

1.2.1 点云分割

理论上，不同分割方法的区别主要是测量给定点集相似度，并以此决定分类的方法和标准不同。一旦确定了相似度测量方法，就可以通过测量将相似度在特定阈值内的点分为一组。分割算法主要有基于边缘的、基于曲面的和基于扫描线的三种。

基于边缘的分割方法主要分成两步：边缘检测以及对边界内的点分组。在给定的深度图中，边缘被定义为局部表面属性的变化超出给定阈值的那些点。局部表面属性一般使用曲面法向、梯度、主曲率或高阶导数表示。Bhanu 等[4]提出使用边代替曲面，处理深度图。Sappa 等[5]的方法基于边缘检测策略进行曲面图的快速分割。Wani等[6]针对可重构的多环网提出了一种基于边缘区域的平行分割算法。这些方法都是一些经典的基于边缘的分割算法。

基于曲面的分割方法使用局部曲面属性作为一种相似度测量方法，合并空间位置邻近且具有相似曲面属性的点。分割途径主要有自底向上和自顶向下两种。其中，自底向上的分割原理是从种子点开始，依据给定的相似准则扩展区域，最终的分割结果取决于种子点的选择；自顶向下的方法则一开始将所有点分配到同一组，并逐步为每个点拟合一个曲面单元。Parvin 等[7]的曲面分割方法使用分裂与合并的方式将曲面图分割为诸多平面。同样的问题，Xiang 等[8]则使用分裂-合并的聚类进行分割。然而对于曲面，只要选择的用于拟合该曲面的质量因子高于指定的阈值，则可分割该区域。这样的分割方法对数据中的噪声不敏感，比基于边缘的分割算法性能更好，但同时可能有很大的误差。

第三种基于扫描线的分割方法，主要针对深度图。该分割方法认为深度图的每一行是一条扫描线，在分割的第一阶段独立处理每一条扫描线。Jiang 等[9]提出一种基于扫描线分组的分割方法，对深度图提取平面段。Natonek[10]和 Khalifa等[11]基于此又提出了改进的方法，使用不同方向上的配置文件分割激光扫描数据。

上述这些方法虽各有优点，但应用于散乱点云时，存在以下问题：

(1)很多方法只针对平面，在实际场景中的应用有限。

(2)尽管基于主曲率的方法可以处理有曲对象，但是从散乱点云中估计的曲率不可靠，这会导致严重的过分割。尤其是圆环和球体，很容易出现过分割。Trucco[12]分析了从深度数据中估计的曲率灵敏度，提议至少不应该使用主曲率进行深度数据的平面分割。

(3)很多分割方法需要设置大量的参数，而这些参数对于最终分割的意义和作用并不明朗。一般需使用独立的迭代优化方式进行大量的结果比较，来确定参数的最佳值。

(4)还有有一些方法，如 Marshall 等[13]提出的分割方法，在分割的同时识别表面类型。但是，该方法不适用于本文的先分割再识别的检测流程。

1.2.2 形状检测

形状检测是计算机几何相关领域的常见问题。目前已有很多算法解决这个问题，在此简短地介绍几种重要的形状检测算法。

在计算机视觉中，两个广为人知的形状提取方法是 RANSAC 和霍夫(Hough)变换。两者都可以成功地应用于检测二维和三维形状，甚至对噪声点比例高的输入数据也是可靠的。但是其效率低、时间和空间开销大[14]。

Hough 变换利用点与线的对偶性，使用曲线表达式，将给定的曲线从原始图像空间变换到参数空间。这样就把原始图像中的曲线检测问题转化为寻找参数空间中的峰值问题，也即把整体特性的检测问题转化为局部特性的检测问题。在这种情况下，参数空间的参数量越大，模型越准确。Illingorth 等[15]和 Xu 等[16]提出的 Hough 变换算法主要应用于二维区域。Vosselman 等[17]利用 Hough 变换从三维数据集中提取平面，但参数量小，模型不够准确。

另一种在视觉领域中经常使用的方法是Mediont 等[18]的张量决策体系。该体系能够从极其混乱的场景中成功检测几何表面，方法具有鲁棒性。但是由于无固有模型，所以不能用来检测有预定义类型的原始模型。

Cohen-steiner 等[19]提出一种使用平面拟合进行曲面估计的变形系统。Wu 等[20]使用一些更复杂的形状拟合，扩展了该系统。他们的目的不仅是提取出某个形状，还要找到一个能够表示原型的最优模型。这些方法需要点的连接信息，且由于只使用最小二乘拟合，变形结果容易受噪声点影响而产生错误。

除此之外，在计算机图形学领域，针对点云的混合渲染，Wahl 等[21]提出一种基于 RANSAC的平面检测方法。类似的方法也被 Hofer[23]提出，他使用从几何线元对表面分类的矩阵特征值，进行平面检测。另外有人使用基于 RANSAC的分割算法进行点云的形状检测，这些方法并没有对 RANSAC 框架进行优化或者扩展，主要对包含的点和形状少的模型有效。

1.3 二维标记检测的方法概述

为了设计一种通用的解决方案，我们在此只利用物体的三维几何数据，而不受颜色、纹理的影响。在没有颜色信息辅助下，二维标记在三维数据中很难检测。根据三维激光扫描仪对黑色、反光表面等不敏感，很难捕捉到数据点这一特性，我们采用黑色或者反光表面材质制成的二维标记。具体而言，本文使用一张黑色的圆形薄纸片作为二维标记。由激光扫描仪 Mantis 获取的三维点云数据显示，该二维标记的形状为空心圆。本文仅使用物体的三维几何信息，因此二维标记的检测问题就转化为二维形状的检测问题。根据本文二维标记在点云中的分布特点，即：空心圆的内部无数据或极少数据，而圆外数据分布密集，提取该标记的边缘点并检测圆环，即可得到该标记。

本文提出了可在三维点云中有效检测二维形状的方法，步骤如下：

(1)在场景中添加二维标记；

(2)对点云数据进行预处理；

(3)根据点云数据，将数据分割为不同段；

(4)利用扩展 RANSAC 算法检测二维标记。在检测过程中，先检测标记所在的数据段，再提取该段的边缘，最后检测圆环，即得二维标记。

2 二维标记检测的技术实现

2.1 检测概述

本文旨在为场景提供清晰的辨识，主要为了解决场景缺少特征或者特征难以检测的情况。利用在真实场景中放置二维标记作为标记特征，提出一种在三维点云中检测二维标记形状的方法。根据本文的数据特点，检测过程中，首先对点云利用区域生长法进行分割，提取出平面边缘；然后利用扩展的 RANSAC 进行检测。具体流程如图 1 所示。

图 1 二维标记检测流程Fig. 1 Detection process of 2D marker

(1)点云预处理

本文使用激光扫描仪 Mantis，其采集的点云数据量大，且包含大量噪声，因此需要进行点云的下采样、去噪等预处理工作。为了简单有效地进行后续步骤，本文采用均匀下采样以及距离统计去噪音法来进行点云的预处理工作。

(2)点云分割

利用区域生长法对预处理之后的数据进行点云分割。首先使用 k-d 树进行k近邻搜索，估计点云法向。再计算曲率和法向夹角，判断其值是否在给定的阈值范围内，以此进行区域生长的段分割。

(3)二维形状检测

对基于区域生长分割得到的各段点集使用扩展的 RANSAC 进行二维形状检测。在检测形状前，需要先估计二维形状(本文主要涉及平面和圆环，根据实际二维标记形状，也可以使用椭圆或其他形状)。由于基于 RANSAC 分割的分割算法比较适合点和形状少的模型，所以检测二维标记圆之前需要先检测出标记所在的平面，然后使用主成分分析算法(Principal Component Analysis，PCA)提取该平面的边缘轮廓，在此边缘点上检测圆环，即可检测出二维标记。

2.2 技术细节

2.2.1 预处理

(1)下采样

一个场景的点云数据量通常都很大，这也为后续的计算机的计算空间以及时间带来了巨大的负担。为了加快计算速度，以及减少计算机内存占有，一般对原始的点云数据进行下采样。为保证输入数据的相对密度和形状不变，本文采用均匀下采样算法。

对输入的散乱点云中的每个点，在其邻域内搜索k近邻点，去除这些邻近点以实现均匀下采样。该方法的关键在于，如何确定查找k近邻时的搜索范围，以及尽可能最小化该搜索范围，以节约时间，提高效率。

一种有效的用于查找搜索范围和最近邻搜索的方法是划分空间，即对空间点云数据建立 k-d树。k-d 树是一种对k维空间中的实例点进行存储，以便对其进行快速检索的二叉树结构。本文使用三维 k-d 树处理点云。k-d 树沿垂直于相应地轴线的超平面把空间划分为不同的子空间，将所有非叶子节点分割到特定维。

在 k-d 树中为每个点进行k近邻搜索，找到k个最近的点并去除。即每k个点中只保留一个点，数据量缩小为原始数据的 1/k倍。

(2)去噪

激光扫描通常得到不同点密度的点云数据集，且测量误差产生的稀疏噪声点会严重干扰结果。这种对复杂的局部点云特性(如表面法线或曲率的变化)的估计容易产生错误，进而导致无法很好地生成点云。一种行之有效的解决方法是通过对邻近点进行统计，利用统计信息舍弃不符合标准的点。

本文采用基于输入点云与邻点间距离的分布计算的方法进行点云去噪。使用k近邻搜索邻点，k为设定值。对每一个点，计算该点到其所有邻点的平均距离和标准差。假定点云符合一个给定平均值α和标准差σ的高斯分布。根据高斯分布的特性，平均值和标准差由所有点的全局平均距离决定。如果一个点到所有邻点的平均距离和标准差分别超过了α和σ，则被视为噪声点。

2.2.2 点云分割

点云的自动分割为后续物体的识别与检测提供了基础。本文使用一种基于法线平滑度约束的区域生长算法来分割预处理后的点云。该算法比较各点的法线之间的夹角，将在平滑度约束范围内足够接近的点合并为一段。该算法需要先估计每个点的法线和曲率，再基于区域生长进行分割。

(1)法线和曲率的估计

法线的估计需要对每个点的邻点拟合一个平面并计算该点的曲率。该平面的法线即该点的法线，则点的法线估计转化为对该点的邻域拟合所得平面的法线估计。估计平面法线过程需对该点进行k近邻搜索，得到邻点的协方差矩阵，再使用 PCA 计算该矩阵的特征向量和特征值。对每个三维坐标点 ，其协方差矩阵如式(1):

其中，k是点pi邻域内的邻点数；表示邻点的中心；λj为协方差矩阵的第j个特征值；vj即特征向量。

一般地，由于没有数学方法确定法线的符号问题，PCA 估计的法线，其朝向是不确定的，导致整个数据集的朝向也是不连续的。如果视点vp是实际已知的，为了保证所有的法线ni连续地朝向视点，法线需满足如下公式：

(2)区域生长

基于区域生长的分割算法是使用上一步得到的点的法线和曲率。根据设定的参数，按照平滑度约束来分段，并通过以下两个因素避免过拟合：

①局部连通性：被分割在同一个段的点是局部连通的。这一约束通过在区域生长过程使用k近邻查找邻点得以保证。

②曲面平滑度：被分割在同一段的点在局部曲面上应尽可能平滑，这可以通过点的法线与该曲面上其他点的法线的差别来进行判断。用阈值θth和曲率阈值Cth判断某一段的点是否满足平滑条件。

首先对各点的曲率值进行排序。区域的生长过程是从具有最小曲率值的点开始(具有最小曲率的点处在平面的平坦区)。在有序点云中，算法可以不断挑选曲率值最小的点加入段区域中，直到点云中没有可加入到该段的点为止，具体过程如下：

(A)挑选点加入到集合，即种子集；

(B)对于每一个种子点，搜索其邻域点。

(a)对当前种子点的每一个邻点，计算其与当前种子点的法线的夹角，如果夹角小于阈值θth，则将该点加入到种子集；

(b)检测当前种子点的每一个邻点的曲率值，如果曲率小于阈值Cth，则该邻点加入种子集；

(c)将当前种子点从种子集中移除。

(C)重复第(B)步，直到种子集为空，则表示一个区域已经生长完毕。

(D)重复上述步骤，直到没有点需要被划分区域，则所有区域生长完毕，不同的区域即为分割的不同段。

分割结果如图 2(a)所示，分割得到的不同类块用不同的颜色表示。

2.2.3 二维形状检测

(1)形状估计

如前所述，本文需要检测的形状有平面和圆环，下面介绍如何在三维空间用参数估计这些形状。

①平面

在未考虑点的法线时，最小点集 {p1,p2,p3}即可确定一个平面。为了保证生成的平面的合理性，引入三点的法线N1、N2和N3。如果三点的法线偏差小于设定的阈值α，则将该平面加入候选平面集。

②圆环

理论上需要 3 个点来计算出圆环的圆心坐标、法线和半径。这里，我们用 4 个点及其法线来估计圆环。由两点可确定一条直线pi＋λni[4]，则四个点可确定两条交叉直线，并可计算出垂直于直线所在平面的旋转轴。4 点构成两条直线时有几种不同情况，并得到两个不同的旋转轴，我们选择误差最小的轴作为旋转轴。为了得到较小的半径，需先找到绕旋转轴旋转的平面，然后用这个平面上的三个点计算圆环以及圆环上所有点的中心，该中心到旋转轴的距离即为圆环的主半径。

图 2 二维标记检测各部分结果Fig. 2 Some results of 2D marker detection

(2)边缘检测

如形状检测流程，在分割段中找到二维标记所在的平面(即最大的平面)后，由于圆环的特性和使用 RANSAC 在检测形状中的局限性，需要在检测标记圆环之前先提取出圆环所在平面的边缘。

现阶段有大量的算法可以有效地提取出点云的边缘。由于本文涉及的二维标记在点云中为空心圆(其圆形轮廓内没有点，而圆本身是由点包围)，所以 PCA 算法可以有效地提取出空心圆的边缘。

边缘提取过程与 2.2.2 中法线和曲率估计过程类似：找到每个点的邻域，对邻点得到的协方差矩阵计算特征向量及特征值，如公式(1)(2)。根据上述分析，利用 PCA 算法提取边缘，计算出特征值后，利用大特征值与小特征值的比值，进行边缘点的检测(比值大于给定阈值β，则该点是边缘点)。边缘点集合即描述了整个点云数据的边缘轮廓，结果如图 2(c)所示。

(3)RANSAC

RANSAC 是根据一组包含噪声数据的样本数据集，通过迭代方式计算出数据的数学模型参数，得到有效样本数据的算法[23]。这种方法伴随着大量的随机过程，需要进行多次随机运算才能得到最优的结果。

①算法描述

RANSAC 基于以下假设而提出：

(a)数据由“局内点”组成；

(b)“局外点”不能很好地适应需拟合的模型；

(c)除此之外的数据均属于噪声。

算法的输入是一组观测数据，观测数据的参数化模型，以及一些参数。RANSAC 通过反复选择数据中的一组随机子集来达成目标。被选取的子集即为假设的局内点，并用下述方法进行验证：

(a)有一个模型适应于假设的局内点，即所有的未知参数都能从假设的局内点计算得出；

(b)用(a)中得到的模型去测试所有的其他数据，如果某个点适用于估计的模型，认为它也是局内点；

(c)如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理；

(d)用所有假设的局内点去重新估计模型，因为它仅仅被初始的假设局内点估计过；

(e)通过估计局内点与模型的错误率来评估模型。

这个过程被重复执行固定的次数，算法伪代码如下(从点云P中检测并提取形状)：

RANSAC 的核心就是随机性和假设性。加入随机性可以减少计算量，设置循环次数是为了多次计算并选择出最准确的拟合模型；假设性，即认为随机抽出来的数据都是正确的。并以此进行计算，获得其他满足变换关系的点，然后利用投票机制，选出获票最多的一个进行变换。

②模型参数

我们需要根据特定的问题和数据集通过实验来确定参数τ和d，迭代次数k可以根据理论结果设定。当我们估计模型参数时，用ρ表示迭代过程中，从数据集内随机选取出的点均为局内点的概率。随机点生成的结果模型不一定都有用，因此ρ也表征了算法产生的结果成为有用模型的概率。

对(4)式两边分别取对数，得到

值得注意的是，这个结果假设n个点都是独立选择的，即某个点被选定之后，它可能会被后续的迭代过程重复选到，因此这种方法通常是不合理的。由于算法迭代次数k在很大程度上决定了模型的正确率，因此，为了得到更可信的参数，定义k的标准偏差为

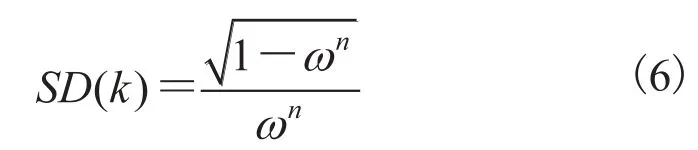
③优缺点分析

RANSAC 的优点是它能鲁棒地估计出模型参数。例如，从包含大量局外点的数据集中估计出高精度的参数。其缺点是计算参数的迭代次数没有上限，如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能是错误的结果。所以 RANSAC 只有一定的概率得到可信的模型，且概率与迭代次数成正比。RANSAC 的另一个缺点是它要求设置与拟合模型相关的阀值。更重要的是 RANSAC 只能从特定的数据集中估计出一个模型，如果存在两个(或多个)模型，RANSAC 只能估计出其中的一个模型，而忽略掉其他。

④检测二维标记

根据 RANSAC 的上述特性和场景特点，本文在使用 RANSAC 算法进行形状检测的过程中还加入了点云分割和边缘提取。本文的形状提取涉及的形状主要是平面和圆环。在进行平面检测时，我们使用的方法是先进行点云分割成段(见2.2.2)，在各个段内分别做 RANSAC 平面检测，这样有效地避免了由于 RANSAC 的随机拟合造成的误差。对于检测圆环过程，先使用 PCA 提取点云边缘(见 2.2.3)，再利用 RANSAC 检测圆环。整个检测过程如图(2)所示。

3 实验结果

本文以一个简单的场景为例(标记圆半径为1.5)，展示检测二维标记的每一步执行的结果(见图 2)。其中，图 2(a)为点云分割结果，不同颜色表示不同分割段。(b)显示从(a)中提取出标记所在的平面。(c)中绿色点为从(b)提取的边缘，从(c)中检测出代表标记的圆环，如(d)中红色点所示。

实验证明，本文提出的方法可以从三维点云中有效地检测出二维标记。相比之下，如果直接使用 RANSAC 算法进行本文的二维标记检测，则可能因标记圆半径较小而无法检测出圆环。且对于半径足够大的圆，由于 RANSAC 算法的正确率具有一定的概率，难以保证检测的正确率。如图 3 所示，(a)中红色点显示本文方法检测出的标记圆。而直接使用 RANSAC 无法检测出本文所示大小的标记圆，且标记圆半径越小，检测难度越大；(b)为直接采用 RANSAC，检测半径为增大一倍的圆形标记的结果。从结果可以看出，本文的标记检测方法有效地避免了RANSAC 的弱点，相对于传统形状检测方法，增强了鲁棒性，能够更加有效地检测出二维标记圆。

图 3 不同算法检测标记圆的结果对比Fig. 3 Comparing the results of different algorithms to detect markers circle

4 讨 论

本文针对缺少特征的场景，提出了一种在三维场景中自主添加二维标记，并基于点云分割和边缘提取的过程，从三维点云中检测该二维标记的方法。实验证明，该方法能够有效地检测出二维标记，而且检测出的二维标记有效减少了物体对原场景的影响，为下一步场景配准、以及识别等提供了关键基础。

本文提出的标记检测方法在检测过程中也存在一定的局限性。以图 2 为例，文中使用的圆形标记比其他形状更容易检测，但是由于圆形的对称和旋转不变的特性，在配准和物体识别等过程中，并不能为场景的辨识提供清楚的方向。另外，本文的 PCA 提取边缘仅使用了点的位置信息，利用空心圆边缘的一侧有邻点，而另一侧邻点极少这一特点进行边缘提取，这种方法简单但不够准确。对于法向变化明显但空间位置连续的不同曲面，难以检测其边缘。另一方面，扫描误差造成的局部点云缺失，会导致边缘提取错误，进而对后面的标记形状检测造成困扰。此外，标记圆的半径越小，检测难度越高。

鉴于以上缺陷，在未来的工作中，我们将尝试更多不同形状的二维标记，使得特征更加鲜明且方向性更强，以便利用局部对应点或关键点搜索。另一方面，使用更加鲁棒的算法提取点云边缘，以降低边缘检测中产生的检测误差。改进后的方法的鲁棒性、适用性更强，可广泛应用于检测、物体识别和数据配准等。

[1] Tinne T, Krystian M. Local invariant feature detectors: a survey [J]. Foundations and Trends in Computer Graphics and Vision 2007, 3(3): 177-280.

[2] Martin H. Marker detection for augmented reality applications [R]. ICG-TR-08/05, Graz: Graz University of Technology, 2008.

[3] Robert AM, John H, David JH, et al. A comparison of 2D-3D intensity-based registration and featurebased registration for neurointerventions [C] // Medical Image Computing and Computer-Assisted Intervention, 2002, 2489: 517-524.

[4] Bhanu B, Lee S, Ho CC, et al. Range data processing: representation of surfaces by edges [C] // Proceedings of the Eighth International Conference on Pattern Recognition, 1986: 236-238.

[5] Sappa AD, Devy M. Fast range image segmentation by an edge detection strategy [C] // Third International Conference on 3-D Digital Imaging and Modeling, 2001: 292-299.

[6] Wani MA, Arabnia HR. Parallel edge-region-based segmentation algorithm targeted at reconfigurable multiring network [J]. Journal of Supercomputing, 2003, 25(1): 43-62.

[7] Parvin B, Medioni G. Segmentation of range images into planar surfaces by split and merge [C] // Conference on Computer Vision and Pattern Recognition, 1986: 415-417.

[8] Xiang RH, Wang RS. Range image segmentation based on split-merge clustering [C] // Proceedings of the 17th International Conference on Pattern Recognition,2004,3:614-617.

[9] Jiang XY, Meier U, Bunke H. Fast range image segmentation using high-level segmentation primitives [C] // Proceedings of the 3rd IEEE Workshop on Applications of Computer Vision, 1996: 83-88.

[10] Natonek E. Fast range image segmentation for servicing robots [C] // IEEE International Conference on Robotics and Automation, 1998, 1: 406-411.

[11] Khalifa I, Moussa M, Kamel M. Range image segmentation using local approximation of scan lines with application to CAD model acquisition [J]. Machine Vision Applications, 2003, 13(5-6): 263-274.

[12] Trucco E, Fisher RB. Experiments in curvaturebased segmentation of range data [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(2): 177-182.

[13] Marshall AD, Luk´acs G, Martin RR. Robust segmentation of primitives from range data in the presence of geometric degeneracy [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(3): 304-314.

[14] Illingworth J, Kittler J. A survey of the hough transform [J]. Computer Vision, Graphics, and Image Processing, 1988, 44(1): 87-116.

[15] Illingorth J, Kittler J. The adaptive hough transform [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(5): 690-698.

[16] Xu L, Oja E. Randomized hough transform (RHT): basic mechanisms, algorithms, and computational complexities [J]. CVGIP: Image Understanding, 1993, 57(2): 131-154.

[17] Vosselman G, Gorte BGH, Sithole G, et al. Recognising structure in laser scanner point clouds [J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2004, 36: 33-38.

[18] Mediont G, Lee MS, Tang CK. Computational Framework for Segmentation and Grouping [M]. New York: Elsevier Science Incorporated, 2000.

[19] Cohen-steiner D, Alliez P, Desbrun M. Variational shape approximation [J]. ACM Transactions on Graphics, 2004, 23(3): 905-914.

[20] Wu JH, Kobbelt L. Structure recovery via hybrid variational surface approximation [J]. Computer Graphics Forum, 2005, 24(3): 277-284.

[21] Wahl R, Guthe M, Klein R. Identifying planes in point-clouds for efficient hybrid rendering [C] // The 13th Pacific Conference on Computer Graphics and Applications, 2005: 1-8.

[22] Hofer M, Odehnal B, Pottmann H, et al. 3D shape recognition and reconstruction based on line element geometry [C] // Proceedings of the Tenth IEEE International Conference on Computer Vision, 2005, 2: 1532-1538.

[23] RANSAC [OL]. [2014-01-30]. http://en.wikipedia. org/wiki/RANSAC.

Two Dimensional Marker Detection in Three Dimensional Point Cloud

LIN Wenzhen HUANG Hui

(Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences,Shenzhen518055,China)

Feature detection plays an important role in object detection and registration. For data registration, correspondences of different frames in the same scene should be found firstly. However, in many cases, there are not effective correspondences, which leads to incorrect registration. One of the effective solutions is to add marker manually in the scene. A method for detecting 2D marker (a black circle drew on paper for scene, hollow circular for point cloud) automatically in 3D point cloud (3D position information only) was proposed. First of all, add a 2D marker in real scene, and divide data set of 3D scene into segments by using region-growing segmentation. Then for each segment, detect 2D marker by extended RANSAC doing shape fitting. By this method, the 2D marker in 3D point cloud could be effectively detected without deforming or changing object. It provides simple and available features for the scene that is lack of features, laying a good foundation for next steps.

segmentation; random sample consensus; shape fitting; 2D shape detection

TP 301

A

2015-01-31

：2015-03-09

林文珍(通讯作者)，硕士研究生，研究方向为计算机图形学，E-mail：wz.lin@siat.ac.cn；黄惠，博士，研究员，研究方向为计算机图形、图像处理和科学计算。