轨道不平顺峰值管理与均值管理的分析

徐金辉，汪力，王源，王平

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031)

轨道不平顺峰值管理与均值管理的分析

徐金辉，汪力，王源，王平

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031)

峰值管理和均值管理是评价轨道平顺状态的常用方法。为对比分析这两种方法的特点，采用傅里叶逆变换反演美国六级高低不平顺轨道谱，用反演的随机样本来分析轨道不平顺截止波长和周期不平顺对两种方法评价结果的影响。研究结果表明:轨道不平顺截止波长对均值管理和峰值管理的评价结果均影响很大，均值管理的稳定性较峰值管理好;峰值管理可以反映出周期不平顺幅值或波长对轨道不平顺的影响，均值管理只能反映周期不平顺幅值对轨道不平顺的影响，无法反映波长的影响。建议制定连续的扣分管理值，以确保峰值管理在不同截止波长下的稳定性;建议在均值管理中引入波长权重。

轨道不平顺 峰值管理 均值管理

轨道不平顺是轮轨系统的主要激扰源，对列车运行的安全性、平稳性、舒适性、车辆和轨道部件的寿命以及环境噪声等都有重要影响［1］，因此，对轨道平顺状态做出科学的评价十分重要。我国常用的轨道不平顺评价方法主要有峰值管理、均值管理和轨道谱。这三种方法中，只有轨道谱从幅值和波长两方面反映了轨道不平顺的统计特征［1］，但是，由于轨道谱缺乏定位功能，在线路养护维修中的应用较为困难。为了克服轨道谱的这个缺陷，我国很多学者将信号处理中的时频分析法运用到轨道不平顺的评价中［2-3］，但这些研究尚处于理论分析阶段，尚未形成成熟的评价体系。

目前，峰值管理和均值管理仍是我国线路养护维修中常用的评价方法。轨道不平顺是一个随机过程，是里程的随机函数，任一特定区段的不平顺可看成随机过程的一个样本［1］。这两种方法对于同一个平稳随机过程能否得出稳定可靠的评价结果，以及这两种评价方法各自的适用范围，国内研究的并不多。

本文用美国六级高低不平顺谱的反演随机样本来分析轨道不平顺的截止波长对峰值管理法和均值管理评价结果的影响，此外还分析这两种评价方法对含有周期不平顺的随机样本的适用性。

1 两种评价方法的特征

1.1 峰值管理

峰值管理是一种反映轨道局部质量状态的方法［4］，通过测量轨道各项几何参数在每个测点的幅值大小，并摘取连续超限测点中的峰值，来判断峰值是否超过规定的限值。我国将超限峰值划分为四个等级，各等级扣分标准:Ⅰ级每处扣1分，Ⅱ级每处扣5分，Ⅲ级每处扣100分，Ⅳ级每处扣301分。每1 km线路评定标准:扣分总数在50分及以内为优良;扣分总数在51～300分为合格;扣分总数在300分以上则为失格［5］。

图1为160＜v≤200 km/h的高低不平顺峰值与扣分数的对应关系。可知，扣分数随峰值的增加呈跳跃式增加，如峰值从11 mm增至12 mm，峰值仅仅增加了1 mm，但扣分数从5分增至100分。

图1 高低不平顺峰值扣分数

1.2 均值管理

均值管理是评价轨道区段整体质量状态的方法［4］，测量并记录轨道区段中全部测点的幅值，计算各几何参数的幅值标准差，同时将单项几何参数的指数进行加权计算获得综合指数，即轨道质量指数(Track Quality Index，TQI)，其管理值见表1［5］。

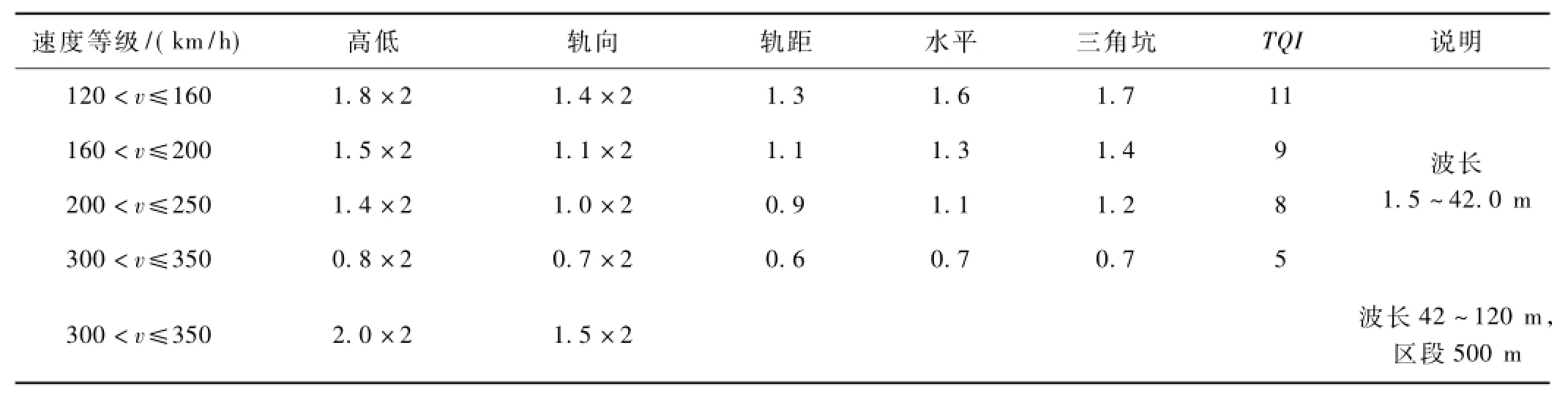
表1 轨道质量指数管理值mm

由表1可知，我国对300＜v≤350 km/h的高速线路制定了1.5～42.0 m和42～120 m两种波长的TQI管理值，对速度为250 km/h以下的线路仅制定了波长1.5～42.0 m的TQI管理值。

2 轨道不平顺随机样本反演

由功率谱密度函数反演轨道不平顺时域样本，国内外最常用的方法主要有二次滤波法、白噪声滤波法、三角级数法和频域法四种方法［6-8］。本文采用文献［8］提出的方法反演美国六级高低不平顺谱，首先根据轨道不平顺功率谱密度与频谱幅值的关系，得出不平顺的频域幅值，并给出随机相位;然后根据实数离散傅里叶变换的实部关于N/2偶对称，虚部关于N/2奇对称(N为频域和时域采样点数)将频谱扩展完整;最后通过傅里叶逆变换得到轨道不平顺的模拟时域样本。图2为美国六级高低不平顺谱的反演样本，图3为美国六级高低不平顺谱与反演样本的模拟谱的比较，可见模拟谱与美国六级高低不平顺谱几乎完全重合。

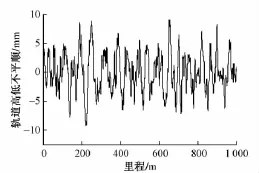
图2 美国六级高低不平顺谱反演样本

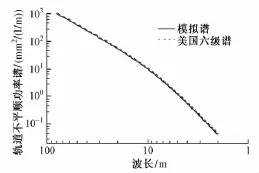
图3 美国六级高低不平顺谱与模拟谱

3 截止波长对两种方法评价结果的影响

轨道不平顺是一个随机过程，理想的评价方法应能够对于同一个随机过程的各随机样本做出稳定的评价结果。

选取反演样本的截止波长为35，45，55，65和75 m进行计算分析，根据评价方法计算单元区段的长度，随机样本的长度取为1 km。

3.1 变异系数

为了便于对比分析，引入统计学中的变异系数(Coefficient of Variation)概念。变异系数是衡量观测值离散程度的统计指标，消除了平均值对数据离散程度的影响，反映了单位均值上的离散程度，变异系数等于标准差与平均值的比。

扣分数的平均值、标准差和变异系数的计算公式如下

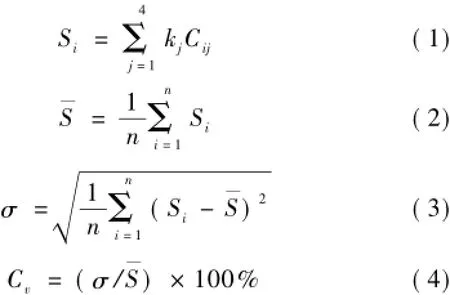
式中:n为单元区段的个数;Si为第i个单元区段的扣分数，kj为第j级偏差的扣分数;Cij为第i个单元区段第j级偏差的个数;为各单元区段扣分数的平均值; σ为扣分数的标准差;Cv为扣分数的变异系数。

TQI的单项几何偏差指数的标准差和变异系数的计算方法与峰值扣分类似，但是式中Si的意义和算法不同，用Sk表示，其计算公式如下

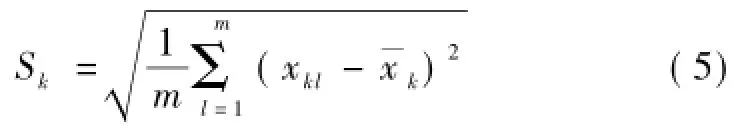
式中:Sk为第k个200 m单元区段的单项几何偏差指数;m为200 m单元区段中数据的个数;xkl为第k个200 m单元区段中第l个采样点的高低不平顺幅值;k为第k个200 m单元区段各采样点高低不平顺均值。

3.2 峰值管理

按照上述分析，可通过计算各随机样本扣分数的平均值和变异系数来分析峰值管理的稳定性。

图4为扣分数平均值随截止波长的变化曲线。

图4 扣分数平均值随截止波长的变化

由图4可知，扣分数的平均值随截止波长增长而增大，且近似呈线性关系。截止波长为75 m时的扣分数是截止波长为35 m时的近11倍。按线路评定标准，截止波长为35 m时线路为优良，截止波长为75 m时线路为合格。可见，截止波长对峰值管理评价结果的影响很大。然而，我国现有峰值管理的扣分标准很单一，v≤200 km/h的线路只规定了一种扣分标准，200＜v≤250 km/h和300＜v≤350 km/的线路也只规定了两种波长下的扣分标准，且两种波长相差较大。建议根据线路速度等级的不利波长范围，制定多种波长下的扣分标准。

变异系数反映了随机样本扣分数的离散程度，变异系数越大表示扣分数越离散，即评价结果越不稳定。图5为扣分数的变异系数随截止波长的变化曲线。

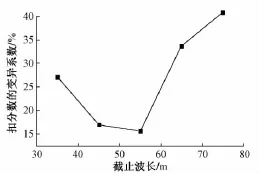
图5 扣分数的变异系数随截止波长的变化

由图5可知，不同截止波长下扣分数的变异系数波动很大，当截止波长为45 m和55 m时，随机样本的变异系数较小，评价结果较为稳定，但在其他截止波长下变异系数均较大，评价结果不稳定。因此可认为，现有峰值管理只能对某波长范围内的随机样本作出稳定的评价结果。这主要是因为峰值管理的扣分标准是离散的，如果随机样本的峰值正好处于各级超限的分界处，就会导致各随机样本的扣分数波动较大。

3.3 均值管理

图6为高低偏差指数的平均值随截止波长的变化曲线。

图6 高低偏差指数的平均值随截止波长的变化曲线

由图6可知，高低偏差指数的平均值与截止波长近似呈线性关系，截止波长为75 m时高低偏差指数是截止波长为35 m时的1.65倍。可见，截止波长对高低偏差指数的影响很大。然而，我国《铁路线路修理规则》中，对于速度250 km/h以下的线路，只规定了单一波长范围(1.5～42.0 m)的管理值，对300＜v≤350 km/h的线路规定了两种波长范围的管理值。

图7为高低偏差指数的变异系数随截止波长的变化曲线。

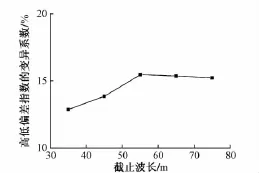
图7 高低偏差指数的变异系数随截止波长的变化曲线

由图7可知，变异系数随截止波长的变化很小，正负波动仅在1.3%左右，可认为均值管理的评价结果的稳定性不受轨道不平顺截止波长的影响，均值管理的评价结果比峰值管理的评价结果更为稳定。这主要是因为均值管理将所有测点的幅值都作为元素参与计算，随机样本的幅值分布较峰值分布更为稳定。因此，在对现有均值管理进行完善和改进时，只需考虑均值管理与截止波长的关系，不用考虑截止波长对其稳定性的影响。

4 周期不平顺对两种方法评价结果的影响

各国的轨道不平顺标准谱都是根据大量实测数据拟合出的一个平滑曲线，只描述了不平顺的宽带随机波特征，忽略了轨道不平顺中的窄带随机波和周期不平顺。但是，在实际的轨道不平顺中常常含有窄带随机波和周期不平顺，因此，理想的评价方法应能够对含有窄带随机波和周期不平顺的轨道结构做出准确的评价。本文以含有周期不平顺的随机样本为例，分析峰值管理和均值管理的适用性。

轨道不平顺的周期不平顺主要包括:由扣件间距引起的波长为0.625 m整倍数的周期不平顺;由轨道板长度引起的波长为5.0 m和6.5 m的周期不平顺;由养护维修引起的波长为10 m和20 m的周期不平顺;由钢轨定尺长度引起的波长为12.5 m和25.0 m的周期不平顺;由简支梁长度引起的波长为32 m的周期不平顺等。

任取一个长度1 km、波长范围为2～50 m的反演随机样本与周期不平顺叠加。为了简化计算，采用正弦函数表示周期不平顺。周期不平顺的波长分别取为5，10，20，25和32 m，幅值分别取为1，2，3，4，5和6 mm。

4.1 峰值管理

未叠加周期不平顺的美国六级谱反演样本的扣分数为27，叠加周期不平顺后随机样本扣分数的计算结果如表2所示。

表2 峰值管理的扣分数

由表2可知:①周期不平顺波长一定时，扣分数随着幅值呈非线性增大，可见峰值管理能够反映周期不平顺幅值对轨道平顺性的影响。②周期不平顺幅值一定时，计算结果基本上呈现出波长越长扣分数越小的规律。这主要是因为幅值一定时周期不平顺的波长越长其峰值个数越少，则扣分数也越小。反之，波长越短则扣分数越大。③周期不平顺波长和幅值均不同时，扣分数无法进行比较。如周期不平顺波长为5 m幅值为3 mm时扣分数为145，波长为25 m幅值为5 mm时扣分数为147，这两种周期不平顺的波长、幅值以及1/4波长变化率［1］相差很大，但得到的评价结果却很相近。

综上可以得出，峰值管理可以反映出周期不平顺幅值或者波长对轨道平顺性的影响规律，但不能反映出幅值和波长的综合影响规律。

4.2 均值管理

未叠加周期不平顺的美国六级谱反演样本的高低偏差指数为2.56，叠加周期不平顺后随机样本均值管理的计算结果如表3所示。

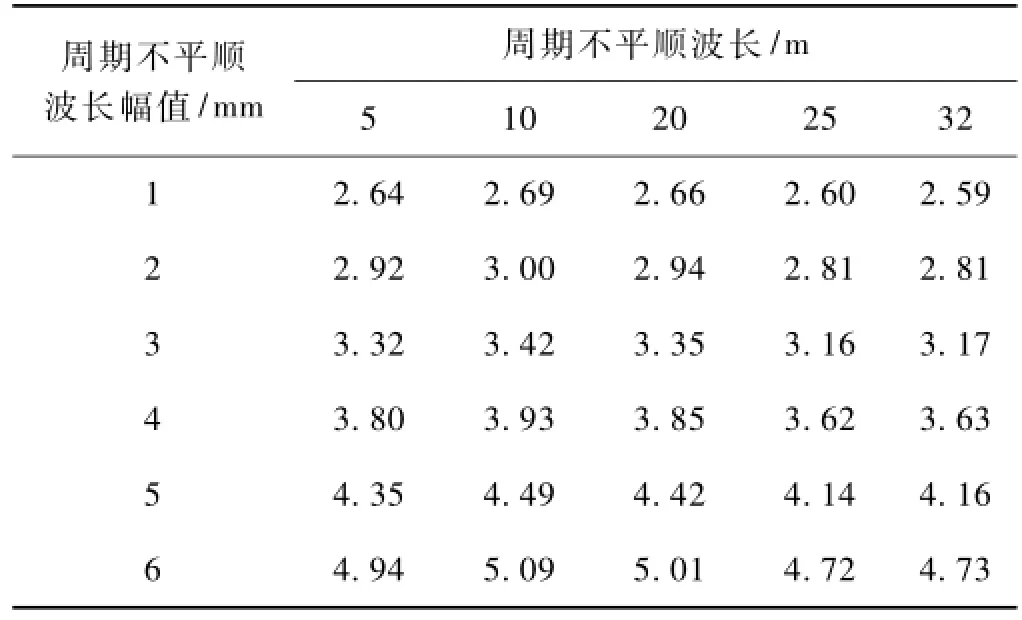
表3 均值管理计算结果mm

由表3可知:①周期不平顺波长一定时，轨道高低偏差指数随幅值的增大呈非线性增大，与峰值管理类似，均值管理能够反映周期不平顺幅值对轨道平顺性的影响。②周期不平顺幅值一定时，轨道高低偏差指数随波长的增长无明显的变化，如周期不平顺的幅值为6 mm时，波长为5 m时高低偏差指数为4.94 mm，波长为32 m时其高低偏差指数约为4.73 mm，相差仅0.21 mm。

可认为，均值管理只能反映周期不平顺幅值对轨道平顺性的影响，无法反映波长的影响。对于含有大量周期不平顺线路，均值管理无法作出准确的评价。

5 结论

通过对峰值管理和均值管理评价结果的分析，可以得出以下结论:

1)轨道不平顺截止波长对均值管理和峰值管理的评价结果都有很大的影响，但不同截止波长峰值管理评价结果的变异系数波动很大，均值管理评价结果的变异系数较为稳定，说明均值管理具有较好的稳定性。

2)对于含有周期不平顺的轨道线路，峰值管理可以反映出周期不平顺幅值(或者波长)对轨道平顺性的影响规律，但不能反映出幅值和波长的综合影响;均值管理只能反映周期不平顺幅值对轨道平顺性的影响，无法反映波长的影响。可见，对含有周期不平顺的线路，峰值管理的适用性优于均值管理。

3)轨道不平顺的管理应同时兼顾峰值管理和均值管理，现有峰值管理和均值管理均存在不足，需要对其做进一步完善和改进。

4)建议根据扣分数的平均值与截止波长的关系制定不同截止波长时的扣分管理值，并制定连续的扣分管理值，以确保峰值管理在其相应波长范围内的评价结果是稳定的;改进现有均值管理方法时，应引入波长权重。

［1］罗林，张格明，吴旺青，等.轮轨系统轨道平顺状态的控制［M］.北京:中国铁道出版社，2006.

［2］陈宪麦，王澜，陶夏新，等.基于小波分析理论的轨道不平顺分析［J］.铁道工程学报，2008(1):57-61.

［3］张洁，陈春俊，林建辉.基于小波变换的轨道不平顺信号分析［J］.西南交通大学学报，2004，39(4):469-471.

［4］翁绍德，李志隆，杨凤春，等.轨道质量指数的基本概念及计算机处理技术［J］.铁道建筑，1994(8):22-27.

［5］中华人民共和国铁道部运输局.运基线路［2009］41号既有线轨道不平顺质量指数标准及管理暂行办法［S］.北京:中华人民共和国铁道部运输局，2009.

［6］陈春俊，李华超.频率采样三角级数法模拟轨道不平顺信号［J］.铁道学报，2006，28(3):38-42.

［7］王元丰，王颖，王东军.铁路轨道不平顺模拟的一种新方法［J］.铁道学报，1997，19(6):110-115.

［8］陈果，翟婉明.铁路轨道不平顺随机过程的数值模拟［J］.西南交通大学学报，1999，34(2):138-142.

Analysis on management of peak and standard deviation for track irregularity

XU Jinhui，WANG Li，WANG Yuan，WANG Ping
(MOE Key Laboratory of High-speed Railway Engineering，Southwest Jiaotong University，Chengdu Sichuang 610031，China)

Peak m anagem en t and standard deviation m anagem en t are comm on m ethods to evaluate track irregularity.In order to analyze the characteristics of these tw o m ethods，the paper inversed the Am erican sixth-level vertical profile irregu larity track spectrum by inverse Fou rier transfo rm，the inf luence of cu toff w avelength of track irregularity and periodic irregularity on the two evaluation methods was analyzed by random samples of inversion.T he resu lts show ed that the cutoff w avelength of track irregularity has a significant im pact on the evaluation resu lts o f these tw o m ethods，standard deviation m anagem en t is m ore stable com pared w ith peak m anagem en t，peak m anagem ent can reflect the in fluence of am p litude or wavelength of period ic irregu larity on track irregularity，standard deviation m anagement can only reflect the in fluence of am plitude which cannot reflect the in fluence o f w avelength.It is recomm ended that a con tinuous value deduction m anagem en t shou ld be form ulated to ensu re the stability of peak m anagem ent w ith d ifferent cu toff wavelength，and w avelength weigh t should be introduced in the standard deviation m anagem en t.

T rack irregu larity;Peak management;Standard deviation management

U216.4

A

10.3969/j.issn.1003-1995.2015.06.38

1003-1995(2015)06-0147-05

(责任审编李付军)

2014-09-17;

2014-10-20

中国铁路总公司科技研究开发计划项目(2013G009-D)

徐金辉(1987—)，男，河南商丘人，博士研究生。