基于动力总成质心位移及转角控制的悬置系统优化设计

吕兆平吴飞吴川永

（1.上汽通用五菱汽车股份有限公司技术中心；2.湖南大学 汽车车身先进设计制造国家重点实验室）

基于动力总成质心位移及转角控制的悬置系统优化设计

吕兆平1吴飞2吴川永1

（1.上汽通用五菱汽车股份有限公司技术中心；2.湖南大学 汽车车身先进设计制造国家重点实验室）

使用多目标遗传优化算法，在悬置刚度基本不变的情况下，以悬置安装角度为变量，以各自由度方向的解耦率最大及传递到车身侧的动反力最小为目标，对某车型发动机悬置系统进行优化设计。同时对优化前、后动力总成质心位移和转角进行对比，且依据优化结果制作样件并进行测试。结果表明，该方法可以有效控制动力总成在垂直方向的振动和绕曲轴的扭转振动，减少车身振动和降低车内噪声。

1 前言

目前动力总成系统振动控制方法很多，例如固有频率控制法、解耦率方法、悬置动反力最小法等。通过调节系统固有频率，使激励频率高于相应固有频率的倍，并尽量使各个振动模态解耦[1]，该方法主要是控制怠速频率以下的振动。最近有学者[2、3]研究以基于总传递力或动反力最小为目标的设计方法，该类方法能够保证系统具有很好的隔振性能，但其并没有考虑动反力减小后对动力总成运动姿态的影响。

本文建立动力总成悬置系统的6自由度动力学模型，计算悬置系统各个方向上的解耦率和怠速工况下的动反力，以3个悬置动反力之和最小为目标，以前左、右悬置安装角度为主要变量对某车型V型布置悬置系统进行优化，并对优化结果施加路面激励及扭矩激励，考察优化前、后动力总成质心和转角幅频特性的变化情况。

2 悬置系统的解耦率与动反力

将各悬置简化为沿空间3个相互垂直方向（即主刚度方向)上的弹性阻尼元件。动力总成悬置系统将构成一个空间6自由度系统，如图1所示。其中，原点为静止时动力总成的质心；Kui、Kvi、kwi为第i个悬置对应于橡胶悬置弹性主轴u、v、w的主轴刚度。刚体的运动有6个自由度，即x、y、z3个方向的移动x（纵向）、y（横向）、z（垂向）和绕x、y、z轴的侧倾转角θx、俯仰转角θy、横摆转角θz。

其广义坐标为:

利用拉格朗日方程和虚功原理可得动力总成悬置系统的振动方程为:

式中，[M]为系统质量矩阵；[C]为系统阻尼矩阵；[K]为系统刚度矩阵；F(t)为激振力；为6个广义加速度列向量。

悬置优化一般只能对刚度矩阵进行优化，因此仅对刚度矩阵进行推导。

2.1 刚度矩阵[K]的推导

根据力学分析[4]，使悬置移动和转动后，第i个悬置的3个主轴刚度方向所引起的变形分别为Δui、Δvi、Δwi，则系统对橡胶悬置弹性主轴u、v、w的势能为：

对方程分解后为：

故有刚度矩阵为：

研究主要考虑通过优化悬置的安装角度，即优化刚度矩阵[K]中的变换矩阵[Bi]来获得优化结果。试验结果表明，悬置角度优化能够以非常小的成本而取得好的改进效果。

2.2 能量解耦法[1]

能量解耦法是目前悬置参数设计运用较多的方法之一，其假设系统微幅振动（不考虑阻尼），通过合理配置刚度矩阵来实现系统的优化，动力总成悬置系统6自由度线性自由振动微分方程为：

对于式（6），设理论解为：

式中，Xi为理论解的幅值；α为相位角。

将其代入式（6）可得：

即

式中，ω为系统固有频率。

由式（7）可得到悬置系统的圆频率及其振型,当悬置系统以第i阶主振动时，第k个广义自由度上分配到的能量所占悬置系统总能量的百分比Tpki（表征解耦程度的高低）为：

式中，mkl为[M]的第k行l列元素；φi为系统的i阶主振型；分别为φi的第k和第l个元素。

2.3 悬置动反力与质心位移计算

在怠速工况下，发动机悬置系统的振动微分方程为：

在悬置动反力和质心加速度计算过程中，系统阻尼矩阵对计算结果存在较大的影响，不能忽略。

系统受迫振动时的稳态解为：

第i个悬置传递给车身的动反力{}fi可以表示为：

式中，[ki]为第i个悬置在全局坐标系中的刚度矩阵；[ri]为第i个悬置位置坐标的反对称矩阵。

怠速工况下悬置系统传递给车身的动反力之和为：

式中，fix、fiy、fiz分别为第i个悬置在怠速工况下动反力的3个分量。

3 基于动反力最小的多目标遗传优化

NSGAⅡ是一种基于Pareto最优解概念的多目标遗传算法，已应用于多材料、多规格组合和多目标优化中。基于NSGAⅡ求解发动机悬置系统的多目标优化问题的应用见文献[5]，其在拓扑优化和汽车车身分块等领域中也有应用[6]。

定义目标函数为怠速激励情况下所有悬置动反力之和。所研究车型发动机怠速转速为750 r/min，以怠速频率为25 Hz下的动反力最小为目标，以V型布置前左、右悬置夹角为设计变量，使其在15°～45°之间变动，通过编制Matlab程序集成ISIGHT进行优化，使用NSGAⅡ多目标遗传算法自动推荐一组最优解。

4 优化设计实例

4.1 原车型悬置系统分析

该发动机悬置系统换装动力总成后出现怠速抖动大、噪声无法达到目标值的现象。两个动力总成的质量和转动惯量对比如表1所列，可知两者差别较大。由于动力总成转动惯量的差异，借用原动力总成悬置系统刚度及安装角度（表2）进行计算，得到各阶固有频率和能量分布百分比如表3所列，此时动反力F=720.7 N。

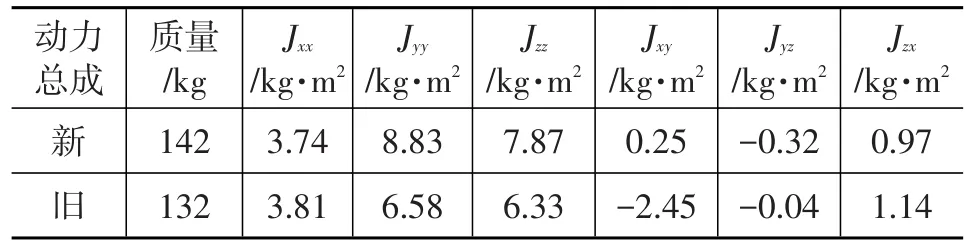
表1 新、旧动力总成质量及转动惯量对比

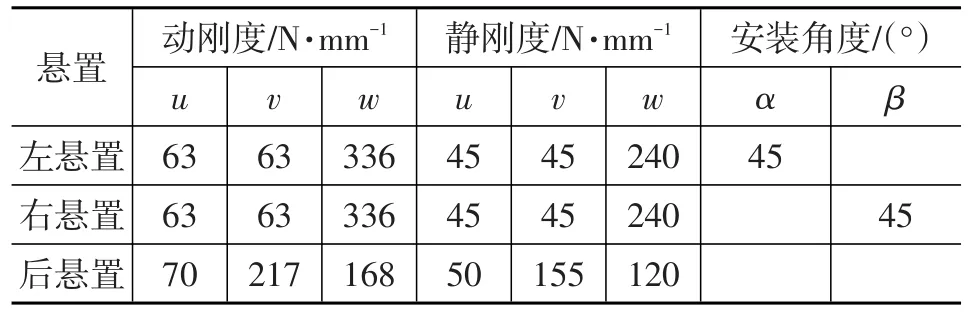
表2 原悬置系统主轴刚度(局部坐标系)及安装角度

表3 原悬置系统在新动力总成参数下的解耦率及固有频率

表3为计算得到的动力总成刚体在6个方向振动的固有频率和能量分布。由表3可知，动力总成系统在垂直方向的解耦率为77.94%；动力总成绕曲轴方向振动的频率为18 Hz，远远高于设计目标，解耦率为26.54%，该方向的振动和绕z向模态耦合严重；另外，z向和侧倾，横摆向和y向也存在较为严重的耦合情况。对动力总成施加单位路面激励（1N）和绕曲轴扭转方向扭矩激励200 N·m，得到动力总成平动及转动幅频特性如图2所示[7]。由图2可知，在路面激励的情况下，动力总成垂直方向的位移为11.5 mm，位移过大；在扭矩激励的情况下表现更加恶劣，动力总成绕曲轴方向平动位移超过35 mm，而角位移幅频特性峰值也超过14°。此为导致整车怠速振动噪声不能达标的主要原因。

4.2 系统优化及分析

将悬置刚度变动范围设定为±15%，V型悬置的安装角度为15°～45°。对该悬置系统采用多目标优化设计方法进行优化，优化后左悬置的安装角度由45.0°变为22.7°，右悬置的安装角度由45.0°变为25.7°，优化后的刚度参数如表4所列。优化后得到的系统固有频率和能量分布百分比如表5所列，此时动反力F=621.2 N，比原方案有较大下降。

表4 优化后悬置系统主轴刚度（局部坐标系）及安装角度

表5 优化后悬置系统解耦率及固有频率

由表3和表5可以看出，对悬置安装角度进行调整后提高了悬置系统的隔振性能。优化后悬置系统侧倾方向固有频率由18 Hz下降到9 Hz，解耦率从26.54%提高到71.93%，与横摆模态的耦合大有改善。其它方向的能量分布百分比也都有一定程度的提高，特别是y向和绕z轴方向。系统实现了6个自由度方向的近乎完全解耦。对动力总成施加单位路面激励和绕曲轴扭转方向扭矩激励200 N·m，得到优化后悬置系统动力总成平动及转动幅频特性如图3所示。

动力总成角位移的幅频特性曲线中，在10.2 Hz处均出现峰值。由图2b和图3b可知，动力总成角位移的幅值均很小。优化前、后动力总成质心在路面激励下的平动位移及转动角度变化不大，仅平动幅值有所降低，z向平动位移从11.5 mm降低到10.5 mm。

从表3可知，由于悬置系统在俯仰方向和横摆方向的振动是严重耦合的，在侧倾方向力矩的作用下，优化前悬置系统的动力总成在y方向振动的位移在6.4 Hz处峰值最大达到35 mm（图2c）；同时，在侧倾方向的角位移也比较大，在6.4Hz处角位移达到了14.4°。优化后悬置系统的动力总成在y方向振动的位移由35 mm下降到6 mm（图3c），侧倾方向的角位移也由14.4°下降到9°（图3d）。

4.3 样件制作及实测验证

根据优化结果制作样件并进行整车振动测试。优化前、后怠速前排噪声对比如图4所示。优化前、后怠速驾驶员座椅导轨及转向盘振动对比如图5所示。可知，怠速时车内噪声降低2.8 dB（A），座椅导轨振动降低50%，转向盘振动降低70%。

优化前、后3挡WOT工况下前排噪声及语音清晰度对比如图6所示。可知，该工况下低转速车内噪声降低2～6 dB（A），语音清晰度提高20%。

优化前、后3挡WOT工况驾驶员座椅导轨及转向盘振动对比如图7所示。可知，该工况下座椅导轨振动降低30%，转向盘振动降低60%以上。

5 结束语

以某V型布置动力总成悬置系统为研究对象，通过商业软件ISIGHT和Matlab的集成，利用多目标优化计算方法NSGAⅡ对橡胶悬置系统的解耦率和动反力进行优化，同时还利用Matlab编程对模型施加路面激励及绕曲轴扭转方向的激励，考察优化前、后动力总成质心和转角幅频特性的变化情况，最后依据优化方案进行样件试制并测试验证。验证结果表明，该方法能从一定程度上解决能量解耦法及动反力最小为目标的设计方法的局限性，同时还能缩短方案验证时间及修模成本。

1 吕兆平.能量法解耦在动力总成悬置系统优化设计中的运用.汽车工程，2008（6）：523～526.

2 周冠南，蒋伟康,等.基于总传递力最小的发动机悬置系统优化设计.振动与冲击，2008（8）：56～58.

3 谢展，于德介，李蓉.汽车发动机悬置系统的多目标稳健优化设计.汽车工程,2013（10）：893～897.

4 赵艳杰，陈翀.基于Matlab的动力总成悬置系统参数优化设计.机械设计，2009,26（8）:62～65.

5 吴飞，等.综合考虑解耦率和隔振率的发动机悬置系统多目标优化.汽车工程，2013（1）：18～22.

6 胡朝辉.多材料——多零件规格组合结构多目标优化的应用研究.机械工程学报，2010，46（22）：111～116．

7 上官文斌,黄天平，徐驰，等.汽车动力总成悬置系统振动控制设计计算方法研究.振动工程学报，2007，20（6）：577～582.

（责任编辑晨 曦）

修改稿收到日期为2015年5月1日。

The Optimization Design of Engine Mount System Based on Displacement&Angle Control of Powertrain COG

Lv Zhaoping1,Wu Fei2,Wu Chuanyong1
（1.SAIC GM Wuling Automobile Co.,Ltd Technical Center.2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University）

A vehicle engine mount system is optimized using the multi-objective genetic optimization algorithm, where the mount installation angle is chosen as main variables with the engine mount stiffness essentially unchanged,and the maximization of decoupling rate of various DOFs and the minimization of the dynamic reaction force transmitted to vehicle body are considered as the objectives.The powertrain centroid displacement and angle is compared before and after optimization.Finally,some samples are made according to optimization and tested.The test results show that this method can effectively control vertical vibration of the powertrain and torsional vibration around crankshaft,thus reducing car body vibrations and interior noise.

Powertrain，Engine mount system，Displacement of COG，Angle，Optimization design

动力总成 悬置系统 质心位移 转角 优化设计

U464

A

1000-3703（2015）09-0036-05