双足被动步行的全局稳定性分析

胡峻峰,曹 军

(东北林业大学机电工程学院,哈尔滨150040)

双足被动步行的全局稳定性分析

胡峻峰,曹 军

(东北林业大学机电工程学院,哈尔滨150040)

在经典双足被动步行动力学模型的基础上,分析环境和力学参数影响下机器人被动步行的全局稳定性。计算不同模型参数下被动步行稳定不动点,采用胞胞映射计算得到不同模型参数下该动力学模型稳定单周期步态的吸引区域。研究发现双足被动步行的鲁棒性与其环境、力学参数关系密切,同时提出估计不动点吸引域形状的2个度量:最小半径与最大半径。实验结果给出被动步行稳定区域与斜坡倾角和质量比值的关系,同时通过分析某些偏离不动点较大的稳定吸引胞,以及吸引域的最小半径与最大半径的变化趋势,反映了双足被动步态的鲁棒性。

双足被动步行;全局稳定性;胞胞映射;不动点;吸引域;鲁棒性

1 概述

传统主动双足机器人[1]尽管智能化程度高,能完成的动作多,可自主或受控改变行走速度和方向,但其结构复杂,步态显得很机械,能量消耗大。双足被动步行机器人充分利用自身机构固有的自然动力学特性,天生具有自然的步态,以及与人类步行相似的能量效率,迅速成为双足机器人研究领域的一个崭新且重要的分支。

经过近十年蓬勃发展,当前被动机器人在本体样机设计和研制上种类繁多[2-3],但在行走稳定性方面仍无突破,具体体现在对行走初态的要求苛刻以及系统鲁棒性很差,这与人类自然行走还有很大的差距[4-5]。双足被动机器人要想取得进一步发展,就必须要研究双足步行的内在固有特点,深入研究其控制与稳定性机理,双足被动步行中的稳定性问题[6]主要分为步态局部稳定性与步态全局稳定性两方面,作为双足步行研究的基础,其所得结论可以用来指导双足机器人的设计和控制,实现降低控制器的复杂度和提高机器人整体能量效率。

目前被动行走步态的局部稳定性研究相对成熟,不动点的估计[7]与计算的数值方法[8]已经不少,但是步态的全局稳定性问题[9]研究有待深入,譬如应该如何衡量双足被动机器人在不同参数下的全局稳定性的差异,从而选择合适的参数来设计高效鲁棒性好的被动机器人,另一方面,文献[10]提出分域控制的思想,通过进一步分析机器人的稳定行走的吸引区域,有利于提出高效的全局稳定分域控制切换逻辑。文献[11]等使用胞胞映射定性地刻画出相应被动步行模型的稳定不动点的吸引区域[12]的形状和体积,从而反映在不同参数下满足能让被动机器人稳定行走的初始条件集合的变化情况[13],但是上述吸引区域及机器人在相应模型下的全局稳定性[14]需要进行分析并提取特征。因此,本文通过数值研究,分析讨论在不同环境与力学参数影响下双足被动步行稳定步态[15]吸引区域的差异及演化规律。

2 预备知识

2.1 双足被动步行的动力学建模

将文献[14]的无膝双足被动行走模型作为研究对象,其2条均质刚性直腿有完全相同的质量与几何参数,直腿质心处集中了腿上所有质量,同时髋关节处具有质量,如图1所示。

图1 斜坡上的双足被动步行动力学模型

其中:

在摆动腿触地瞬间,系统的支撑腿与摆动腿发生互换,状态变量发生突变,假设碰撞时间极短且为完全非弹性碰撞,易知在碰撞瞬间双脚都着地,两腿角度满足如下关系式:

根据角动量守恒原理,在碰撞时刻T前后的状态变量满足如下代数方程:

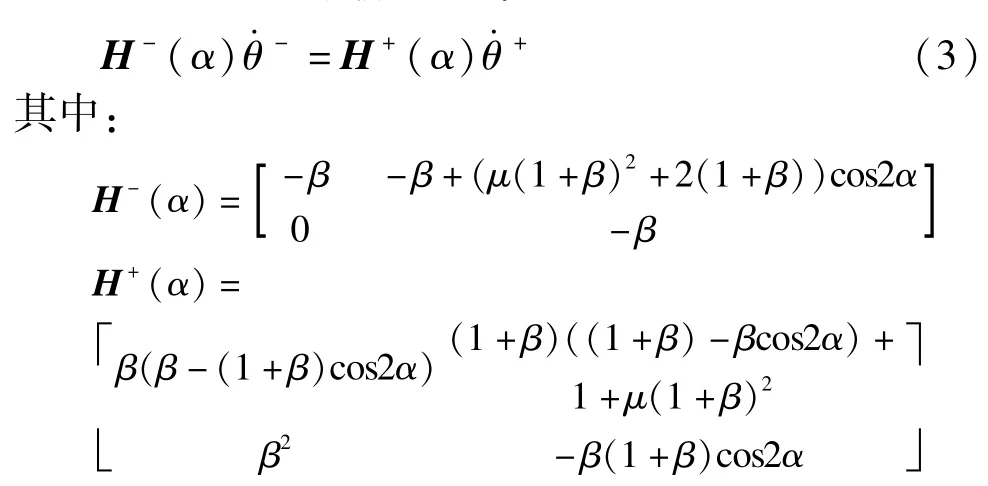
2.2 步态的稳定性分析与计算

文献[5]首先定义并研究了步态的局部稳定性,自其开创性工作以来,研究者一般首先建立步态方程,然后沿用Newton-Raphson方法[5]在预先估计的状态空间里搜索系统的稳定周期解。通过类似方法,建立上述模型的步态方程,见式(1)与式(3),然后以双足着地的碰撞瞬间作为Poincare截面,根据式(2),则2次碰撞之间的过程是一个三维Poincaré映射F,其状态变量Xi∈R3,i=1,2,…,n,可知Xi+1=F(Xi),若F(X∗)=X∗,则周期步态存在,此时庞加莱映射的固定点X∗称为不动点,以稳定的不动点作为步态初值,机器人行走会呈周期步态。然而机器人具有局部稳定性,仅能说明机器人可以形成稳定的行走状态,而机器人行走的初始条件偏离其稳定不动点多大范围内仍能形成稳定行走状态,需要对其进行全局稳定性分析。全局稳定性越好,鲁棒性越好,满足稳定行走的初始条件的范围越大,被动机器人稳定行走抗干扰的能力就越强。满足能让被动机器人形成稳定步态的集合称为不动点的吸引域,把吸引域内的点作为双足被动步行机器人的初始条件,经过有限步运动以后都将收敛到稳定运动状态。因此,可以用吸引域的大小等特征来分析双足被动机器人的全局稳定性。

文献[12]在上述局部稳定性研究方法上进行了扩展,采用胞胞映射方法在Poincaré像空间上找到不动点的吸引域。为了衡量双足被动步行系统在不同参数下的鲁棒性以及给后续控制算法提供理论支持,定义吸引域最小半径Rmin与最大半径Rmax。

设在Poincaré像空间上取一初始状态集S,Σ是其内部稳定不动点的吸引点集,易知Σ⊂S,将任意点Y与稳定不动点Y0之间的距离定义为d=Y-Y0,S中任意满足d≤Smin的初始状态变量Y都能收敛到稳定不动点上。在初始状态空间中满足d＞Smax的任意初始状态变量Y肯定无法收敛到稳定不动点上。可见,吸引域最小半径Smin反映了双足被动机器人在初始状态偏离不动点多大程度时经过有限步以后必定可以回到单周期稳定步态。

而吸引域最大半径Smax反映了机器人在初始状态偏离不动点多大程度时仍旧有可能经过有限步回到单周期稳定步态。

3 数值实验与分析

3.1 实验环境

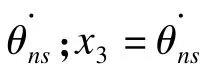
文献[10]中发现,被动步行行走过程对环境扰动的鲁棒性是由机器人的力学参数和斜面坡度共同决定。下面分析质量参数μ,斜面坡度φ的变化对稳定不动点吸引域的影响。

3.2 参数μ对稳定步态吸引域的影响

采用前述Newton-Raphson迭代方法求取了μ=1∶ 0.1∶10下的稳定不动点变化情况,在参数连续变化时,系统的稳定不动点的变化也是连续的,而且随参数μ的增大,稳定不动点的变化越来越小,如图2所示。

图2 参数μ从1增加到10时的系统稳定不动点

在上述胞化的初始状态空间里,利用胞映射法求取了不同的参数μ下吸引到其对应的稳定不动点的初始状态胞,其中,μ=1,2,4,6,8下的吸引域如图3所示。

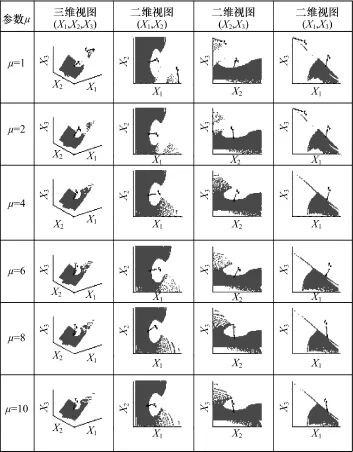
图3 随参数μ从1～10变化时稳定不动点的吸引域

如图3所示,随参数μ的增大,稳定不动点的吸引域的体积在μ=3时明显变大,然后继续变大,可见双足被动机器人的髋关节重量相对腿重量越大,其鲁棒性越好,而且在比值大约为3时,其稳定性区域就可以达到较理想的程度,这与人类身体结构重量分配的常识也是一致的。在图中取μ=1时的不动点的吸引区域一远端点Ym=[0.696 39, -2.932 5,2.812 5],对其进行迭代,发现其在迭代次数n≤20时就可以迅速收敛到不动点Y0= [-0.295 69,-0.362 84,-1.1063],如表1所示。

表1 吸引点Ym的收敛情况

由表1可知,如果双足被动机器人的初态哪怕偏离稳定步态很远,如果合适的话,恢复到稳定状态的过渡时间T与状态偏差d收敛很快,因此,可以迅速回到稳定的单周期步态。通过观察图3发现,这样的点与摆动腿角速度的正负有关系,如果摆动腿的角速度为正,且足够大的话,那系统就有足够的机会回到稳定步态。随后,估算随参数μ变化,稳定不动点吸引域的最小半径与最大半径如图4所示。

图4 吸引域的最小半径与最大半径

由图4可知,在参数μ增加时,双足被动步行机器人的鲁棒性越来越好,在μ≈7时,步行机器人肯定可以承受最大偏离程度的扰动,但是此时最大半径较小,如果偏离较大,需要消耗更多能量镇定到离其最近可以调整到稳定步态的状态上。而在参数μ≈2时,即使步行机器人受到的扰动较大,但是仍旧在最大半径所包含的范围内,仅需少许能量就可以将其状态镇定到距离其最近的吸引点上,因此,有利于工程实现与设计。

3.3 斜坡倾角φ对稳定步态吸引域的影响

采用前述Newton-Raphson迭代方法求取了φ= 0.25°∶0.25°∶4°下的稳定不动点的变化情况,由图5可知,随倾角变化,稳定不动点在相空间中的变化也是连续的。

图5 参数φ从1增加到10时的系统稳定不动点

在上述胞化的初始状态空间里,利用胞映射法求取了不同斜坡倾角φ下吸引到其对应的稳定不动点的初始状态胞,其中,φ=0.25°,1°,2°,3°,4°下的吸引域如图6所示。从图6可以看出,随倾角φ的增大,稳定不动点的吸引域的体积在φ=3时明显变大,然后继续变大,可见斜坡倾角在合适的范围内相对较大时,双足被动机器人的鲁棒性更好,而且在比值大约为3时,其稳定性区域就可以达到较理想的程度。

随后,也同时估算了随倾角φ变化,稳定不动点吸引域的最小半径与最大半径,如图7所示。

图6 随参数φ从0.25°到4°变化时稳定不动点的吸引域

图7 吸引域的最小半径与最大半径

可知在斜坡倾角φ增加时,双足被动步行机器人的吸引区域越来越大,随斜坡倾角的增大,其吸引域的最大半径与最小半径增长较快,系统的鲁棒性越来越好,但是斜坡倾角大于5.07°时会出现复杂的动力学现象[14],如倍周期分岔、混沌等。

4 结束语

本文使用数值方法对不同环境与力学参数下双足被动行走模型的全局稳定性进行了研究与讨论。研究发现,双足被动步行的鲁棒性与其环境、力学参数关系密切,同时提出估算其不动点的吸引区域的最小半径与最大半径对后续的工程设计以及控制策略提供支持,如在环境参数给定的情形下,设计具备与它匹配的力学参数的机器人以获得最大的吸引区域,同时在评估当前控制策略设计是否合理时应该着重考虑2个关键性度量,即吸引区域最小半径与最大半径。下一步工作主要集中在如何高效且精确地计算其不动点的吸引区域以及能量问题。

[1] Sakagami Y,Watanabe R.The Intelligent ASI-MO:System OverviewandIntegration[C]//Proceedingsof InternationalConferenceonIntelligentRobotsand Systems.Piscataway,USA:IEEE Press,2002:2478-2483.

[2] Wisse M.Three Additions to Passive Dynamic Walking; Actuation,an Upper Body,and 3D Stability[C]// Proceedings of International Conference on Humanoid Robots.New York,USA:IEEE Press,2004:113-132.

[3] Collins S H,Ruina A.A Bipedal Walking Robot with Efficient and Human-like Gait[C]//Proceedings of Conference on Robotics and Automation.Piscataway, USA:IEEE Press,2005:1983-1988.

[4] Tedrake R.Stochastic Policy Gradient Reinforcement Learning on a Simple 3D Biped[C]//Proceedings of InternationalConferenceonIntelligentRobotsand Systems.NewYork,USA:IEEEPress,2004: 2849-2854.

[5] McGeer T.Passive Dynamic Walking[J].International Journal of Robotics Research,1990,9(2):62-82.

[6] 毛 勇,王家廒,贾培发,等.双足被动步行研究综述[J].机器人,2007,29(3):274-280.

[7] 苏学敏,赵明国,张 楫,等.被动行走周期性步态不动点搜索的新算法[J].清华大学学报:自然科学版, 2009,49(8):1109-1112.

[8] 柳 宁.双足模型步行中的倍周期步态和混沌步态现象[J].物理学报,2009,58(6):3772-3779.

[9] 倪修华,陈维山.基于BP神经网络的被动步行稳定不动点的估算[J].机器人,2010,32(4):478-483.

[10] Spong M W.Passivity Based Control.of the Compass Gait Biped[C]//Proceedings of IFAC World Congress. Amsterdam,the Netherlands:Elsevier Science Ltd., 1999:19-23.

[11] 曲俊法,双足被动步行机器人行走稳定性的研究[D].哈尔滨:哈尔滨工业大学,2008.

[12] Wisse M,Frankenhuyzen J.Design and Construction of Mike,A 2d AutonomousBipedBasedonPassive Dynamic Walking[C]//Proceedings of Conference on Adaptive Motion of Animals and Machines.Kyoto, Japan:[s.n.],2003.

[13] 柳 宁,李俊峰.用胞胞映射计算被动行走模型不动点的吸引盆[J].工程力学,2008,25(10):218-223.

[14] Goswami A,Thuilot B,Espiau B.Compass-like Biped Robot PartI:StabilityandBifurcationofPassive Gaits[R].HondaResearchInstituteUSA,Inc., Technical Report:INRIA 2996,1996.

[15] 胡运富.无膝双足被动机器人的运动特性和稳定性研究[D].哈尔滨:哈尔滨工业大学,2009.

编辑 顾逸斐

Analysis for Global Stability of Passive Bipeds Walking

HU Junfeng,CAO Jun
(College of Mechanical and Electrical Engineering,Northeast Forest University,Harbin150040,China)

Based on the classical dynamic model of passive biped walking,the globel stability of passive bipeds walking which is influenced by the environment and mechical parameters is discussed.The calculaion about stable fix points on variable parameter is given.Cell-cell map is used to compute the attractive region of the1-periodic steady gait of the walking model with variable parameters.It is found that the robustness of passive bipeds is connected closely to the environment and mechanical parameters.Moreover,this paper also proposes the two metrics to evaluate the shape of attractive region:minimum radius and maximum radius.Simulation results also reveal the relationship between the attractive region of passive walking and the parameters like ground slope or mass ratio.Simultaneously,the robusness of passive biped walking gaits is analyized by special attracive cell and the variable tendency with the maximum reach and the mininum reach of the attractive region.

passive bipeds walking;global stability;cell-cell mapping;fix point;attractive region;robustness

胡峻峰,曹 军.双足被动步行的全局稳定性分析[J].计算机工程,2015,41(2):173-177.

英文引用格式:Hu Junfeng,Cao Jun.Analysis for Global Stability of Passive Bipeds Walking[J].Computer Engineering, 2015,41(2):173-177.

1000-3428(2015)02-0173-05

:A

:TP39

10.3969/j.issn.1000-3428.2015.02.033

中央高校基本科研业务费专项基金资助项目(DL10AB06);国家林业局“948”基金资助项目(2011-4-04);黑龙江省自然科学基金资助项目(QC2012C101)。

胡峻峰(1980-),男,博士研究生,主研方向:人工智能,图像处理;曹 军,教授、博士、博士生导师。

2013-10-08

:2013-12-27E-mail:hujunfeng_2013@126.com