量子进化算法在机器人联盟问题中的应用

李 絮，郭 英，刘争艳

(阜阳师范学院计算机与信息工程学院，安徽阜阳 236037)

量子进化算法在机器人联盟问题中的应用

李 絮，郭 英，刘争艳

(阜阳师范学院计算机与信息工程学院，安徽阜阳 236037)

量子进化算法是一种新的基于量子计算的概率搜素算法，它采用量子比特来编码染色体，采用量子门对种群进行更新进化，具有较快的收敛速度和良好的全局寻优能力。机器人联盟问题是一个复杂的组合优化问题，本文运用量子进化算法对该问题进行算法设计与应用研究，设计了一种量子变异算子，并对算法参数进行了研究。仿真实验结果验证了量子进化算法的可行性与有效性。

量子计算;进化算法;机器人;联盟

在多机器人系统中，受单个机器人能力的限制，机器人之间往往需要相互协作，通过结成联盟才能够完成任务［1］。由于不同的机器人联盟具备的能力不同(成员的数量和能力不同)，且它们执行任务的效率和代价也不相同，在通过联盟完成任务时希望能够以最小的代价获取最大的利益。机器人联盟问题主要研究的就是如何动态生成面向任务的最优机器人联盟，随着系统中机器人数量的增加，可能的联盟总数将会呈指数级增长，因此机器人联盟问题是一个复杂的组合优化问题［2］。

量子进化算法(Quantum-inspired Evolutionary Algorithms，QEA)是近年来发展起来的一种概率进化算法，是量子计算与进化算法相结合的产物［3］。基于量子衍生机制的概率编码方式能够很好的表达不确定信息，同时由于量子具有干涉、纠缠及并行等特性，使得量子进化算法非常适合求解组合优化问题。前期我们在文献［4］中将量子进化算法应用到典型的背包问题中，取得了良好的效果。受可此启发，本文将量子进化算法应用到机器人联盟问题中，并进行仿真实验，实验结果证明了该算法的行性与有效性。

1 机器人联盟问题

1.1 联盟定义

一个机器人联盟就是能够完成任务的一个或多个机器人集合。若系统中机器人集合为R，则定义一个机器人联盟C就是R的一个非空子集。例如，假设机器人集合R={a，b，c}，则可能的机器人联盟C就有如下7个:{a}，{b}，{c}，{a，b}，{a，c}，{b，c}，{a，b，c}。

1.2 问题描述

设n个机器人集合R={R1，R2，…，Rn}，任意机器人Ri都具有一个r维能力向量，其中(1≤j≤r)用于定量描述Ri执行某种特定动作的能力大小［5］。联盟C则具有一个能力向量，BC是联盟中所有机器人能力向量的总和，即。任务t具有一定的能力需求。联盟C能够完成任务t的必要条件是:BC≥Bt，即。

任何一个联盟C都具有联盟代价CostC、联盟收益ProfitC和联盟值ValueC，联盟代价CostC是联盟成员通过联盟活动完成任务的开销总和，联盟收益ProfitC是联盟完成任务获得的利益，而联盟值ValueC则由 CostC和 ProfitC共同确定［6］。机器人联盟问题就是要求出拥有最大ValueC值的联盟。

2 量子进化算法

量子进化算法(QEA)是一种将量子计算与进化算法相结合的概率搜索算法。它以量子计算的一些概念和理论为基础，充分利用量子态的衍生与相干特性，采用量子比特编码来表示染色体，同时利用量子旋转门对染色体进行更新，并保留最优染色体，使算法不断寻优，从而实现对目标问题的优化求解［7］。

2.1 量子比特编码

量子比特是基本的信息存储单元，其状态是由两个基态|0〉和|1〉的任意叠加态构成，一个量子比特状态可表示为

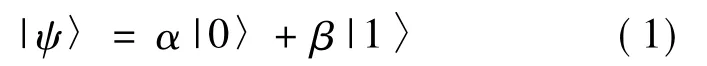
其中，α、β为一对复数，分别表示基态|0〉和

在QEA中，染色体不是采用二进制、十进制或浮点等编码方式，而是采用一种新的量子比特编码方式，称为量子染色体。一个由m个量子比特构成的量子染色体q的表示形式可以描述为

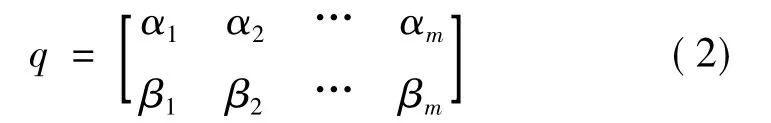
2.2 量子旋转门

在QEA中，采用量子旋转门U(θ)来实现对量子染色体的更新，对量子染色体的更新是通过对每个量子比特的更新来实现的，量子旋转门更新方式表示如下:

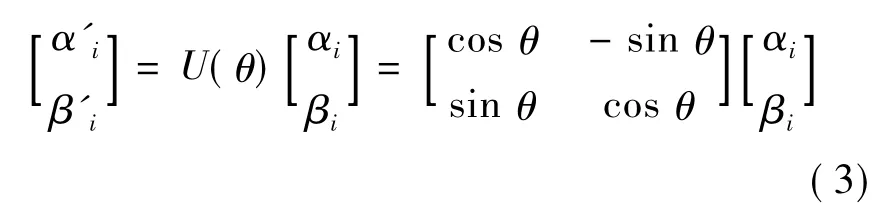
旋转角度θ的大小对种群的更新进化起着关键作用，若θ值太大，能够使种群快速进化，但很可能会早熟收敛于一个局部最优解。若θ值太小，又会使种群更新进化速度较慢，影响算法收敛。

2.3 算法流程

量子进化算法的一般步骤如下:

(1)初始化种群Q(t)，t=0;

(2)测量种群Q(t)，得到一组相应的二进制解P(t);

(3)用适应度函数对P(t)进行评价，并保存最优解;

(4)若满足终止条件，算法结束，否则算法继续;

(5)利用量子旋转门更新;

(6)t=t+1，算法返回(2)继续进行。

其中，在第(1)步初始化种群时，量子染色体的每个量子比特都取1，这意味着所有可能的叠加态以相同的概率出现。在第(2)步中，测量Q(t)生成P(t)的具体操作过程如下:随机产生一个［0，1］之间的随机数，若它大于，则相应二进制解的比特位取1，否则取0。

3 基于QEA算法的机器人联盟优化

将QEA算法应用到机器人联盟问题中，在设计算法优化求解时需要考虑以下几个方面:

(1)联盟编码

设m个机器人集合R={R1，R2，…，Rm}，一个机器人联盟C采用二进制编码，表示为C={r1，r2，···，rm}，每个基因ri(i=1，2，…，m)为0或1。ri=1表示机器人Ri在联盟中，ri=0，则表示机器人Ri不在联盟中。

(2)初始联盟

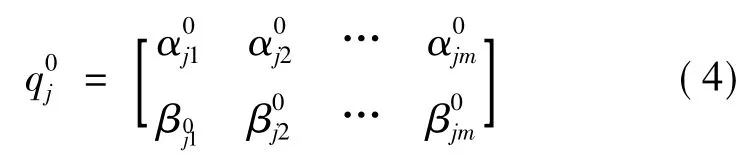
其中，m为机器人个数。

测量种群Q(0)，得到一组相应的二进制解，其中每个pi(i=1，2，…，n)即为一个初始联盟。

(3)适应度函数

机器人联盟问题就是要求出能够以最小代价获取最大收益的最大联盟值。因此机器人联盟问题的适应度函数实际上就是求解联盟值的函数。联盟值ValueC与联盟代价CostC和联盟收益ProfitC有关，它会随着ProfitC值的递增而递增，随着CostC的递增而递减。因此，将适应度函数定义为:F(C)=ValueC=ProfitC/CostC(当联盟C不能完成任务时，ProfitC=0)。用适应度函数对种群中每个联盟进行评价，保留全局最优联盟。

(4)旋转角选择策略

量子旋转门的旋转角通过查表方式获得，具体选择策略如表1所示。

若当前联盟与最优联盟中对应基因位上的二进制值相同，则旋转角度θ为0，否则按照表1对量子比特进行更新操作。

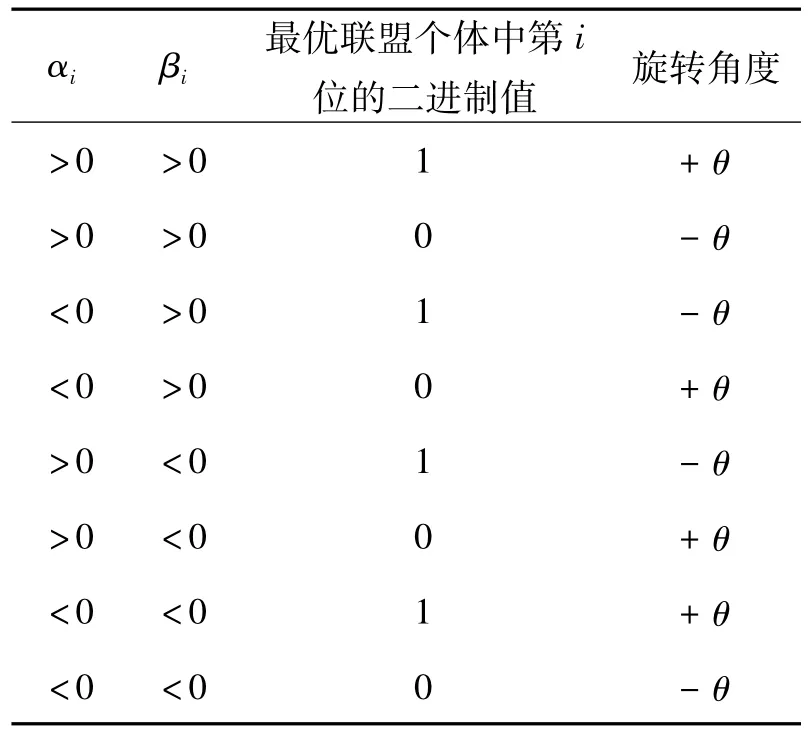
表1 旋转角选择策略

(5)量子变异

为了防止算法早熟收敛，使其能够搜索到联盟问题的真正最优解，本文引入量子非门Unot对量子染色体进行变异操作，即利用量子非门将量子比特概率幅对调。这样就使得原来倾向于坍缩到状态“1”的变为倾向于坍缩到状态“0”，或者相反。量子非门的执行方式如下:

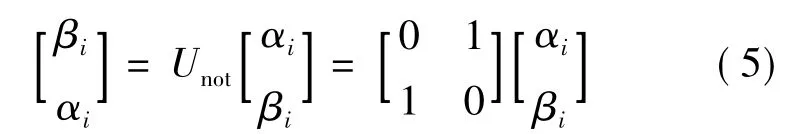
在利用量子旋转门对种群进行更新之后，执行量子变异操作，其具体过程如下:

(i)按照一个给定的变异概率，从种群中随机选择若干量子染色体;

(ii)对选中的量子染色体随机确定一个或多个变异位;

(iii)对选中位的量子比特执行量子非门操作。

4 仿真实验

为了验证基于QEA算法求解机器人联盟问题的有效性，本文设定机器人联盟问题的相关数据如下:设系统中机器人总数为25个，每个机器人Ri具有4种不同的能力，如表2所示。每个机器人Ri需花费的代价为，完成任务t需要4种不同的能力，完成任务t获得的收益为。QEA算法的相关数据如下:种群规模为10，量子变异概率为0.5，最大迭代次数为1 000，为了验证量子旋转门的旋转角度对算法收敛速度和求解质量的影响，将旋转角θ分别取0.001π和0.01π。

针对不同的θ取值，分别运行本文算法各50次，并统计50次实验中算法找到的最优联盟值、最差联盟值、平均联盟值、以及搜索到最优解的次数和最快搜索到最优解的进化代数，结果如表3所示。同时，绘出50次实验中最优联盟值随迭代次数的进化曲线，如图1、图2所示。

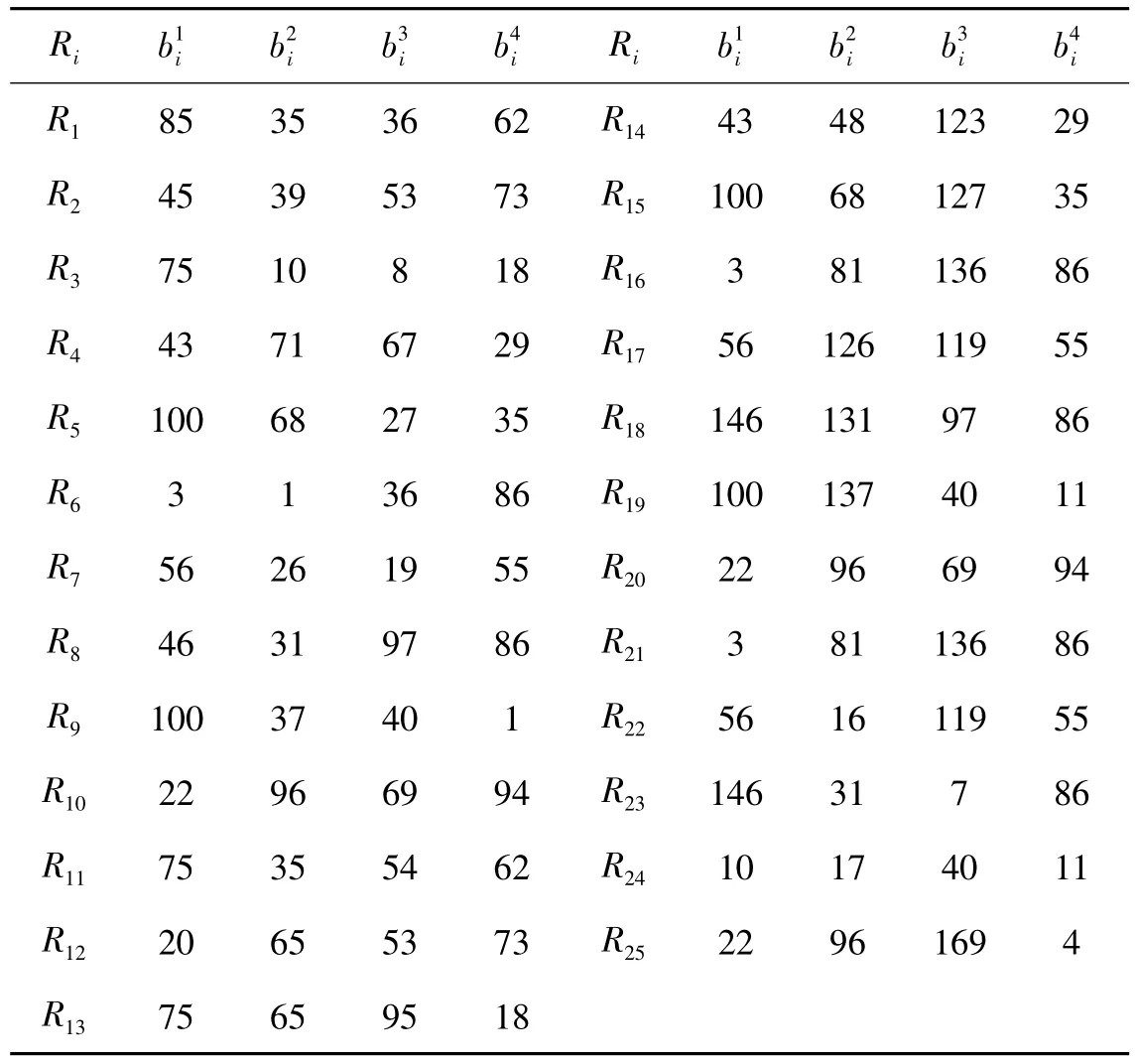
表2 机器人Ri具有的4种能力

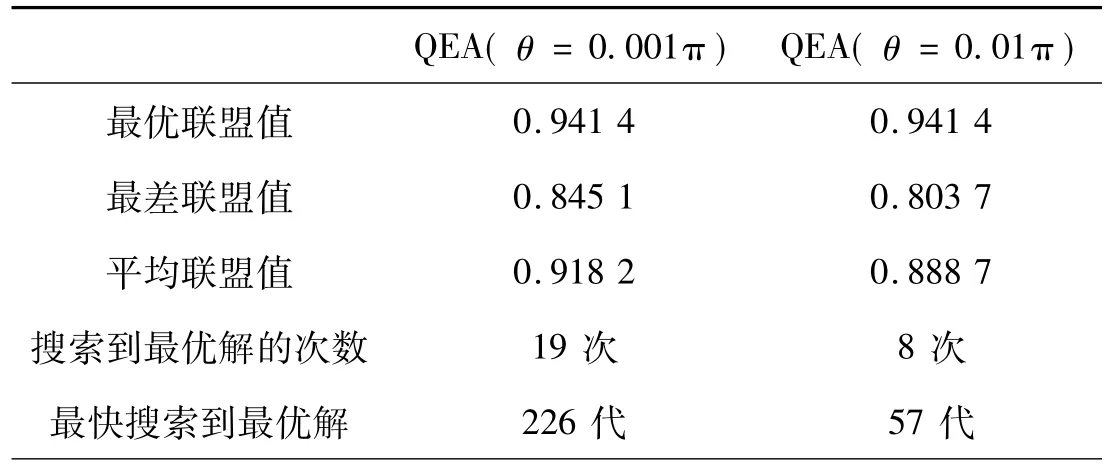
表3 运行不同θ值的QEA各50次的实验结果

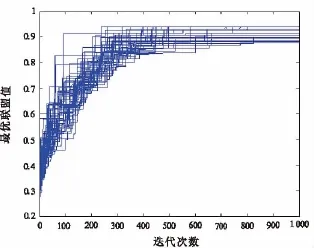
图1 QEA(θ=0.001π)50次实验运行结果

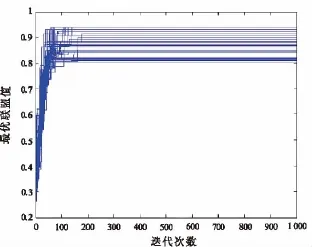
图2 QEA(θ=0.01π)50次实验运行结果

从表3及图1、图2中能够很直观地发现，QEA中旋转角θ取不同的值对算法的收敛速度和求解质量有着明显的影响。θ值较小，使得搜索网格也较小，能够扩大算法的搜索空间，不易陷入局部最优，但同时种群更新进化也较慢，影响算法收敛速度;θ值较大，使得搜索网格也较大，能够使算法在早期快速进化，但很可能会早熟收敛，陷入局部最优解。如表3中所示，θ为0.001π时，50次实验中最快搜索到最优解是在算法进化226代后，而θ为0.01π时，能够在57代就搜索到最优解。从图1和图2中也能明显看到，在算法运行前期，θ为0.01π时收敛速度较快。但同时也能看到，θ为0.01π时算法的求解质量却不如θ取0.001π时。因此，在进行算法应用时，应该根据应用问题是注重收敛速度还是注重求解质量，合理地设置θ值。

5 结束语

机器人联盟问题是多机器人系统研究中一个基础性问题，同时也是一个复杂的组合优化问题。量子进化算法作为一种新的概率搜索算法，采用了量子比特编码方式，使算法具有丰富的多样性和并行性。同时采用量子旋转门和量子非门等寻优机制，利用最优解的信息对种群进行更新进化，使算法具有很好的优化与收敛性能。对机器人联盟问题的研究验证了该算法的可行性与有效性。对该算法的进一步改进，包括进化算子与旋转角的设计，同时进一步扩大其应用领域，将是我们未来的研究工作。

［1］刘淑华，张 嵛，付 帅，等.基于群体智能的多机器人任务分配［J］.吉林大学学报，2010，40(1): 123-129

［2］傅一峰，曹 健，李明禄.面向复杂任务结构的A-gent联盟算法［J］.小型微型计算机系统.2011，32 (3):402-406.

［3］申晓宁，谢文武.基于量子进化算法的移动机器人实时路径规划［J］.计算机科学，2013，40(5):229-232

［4］李 絮，刘争艳.改进的多宇宙并行量子进化算法.计算机工程与应用［J］.2010，46(34):35-38

［5］Travis C，Julie A.Coalition formation for task allocation:theory and algorithms［J］.Auton Agent Multi-A-gent Syst，2011，22(2):225-248.

［6］王 皓，曹 健.分布式环境下面向复杂任务的A-gent联盟构建［J］.计算机工程，2013，39(12):216-221.

［7］钱 洁，郑建国.引入逆学习的量子自适应禁忌搜索算法［J］.电子学报，2013，1(6):1070-1075.

Application of quantum-inspired evolutionary algorithm in robot coalition problem

LI Xu，GUO Ying，LIU Zheng-yan
(School of Computer and Information Engineering，Fuyang Teachers College，Fuyang Anhui236037，China)

Quantum-inspired evolutionary algorithm(QEA)is a new probabilistic search algorithm inspired by quantum computing.It uses quantum bits to encode the chromosomes，and uses quantum gates to update the population，so it has a faster convergence speed and good global optimization capability.Robot coalition problem is a complex combinatorial optimization problem.In this paper，the QEA is used for algorithm design and application research for this problem，and a quantum mutation operator is designed and the algorithm parameters are studied.Simulation results verify the feasibility and effectiveness of the QEA.

quantum computing;evolutionary algorithm;robot;coalition

TP242

：A

：1004-4329(2015)01-049-05

2014-04-23

安徽省教育厅自然科学基金项目(KJ2013Z259);阜阳师范学院自然科学基金项目(2013FSKJ02ZD，2014FSKJ09);阜阳师范学院大学生创新训练项目(FS201310371122);全国统计科学研究重点项目(2014LZ32)资助。

李 絮(1983－)，女，硕士，讲师。研究方向：智能优化。