论Sylow 2-子群是Q8的8p3阶群的构造

陈松良，蒋启燕

(1.贵州师范学院数学与计算机科学学院，贵州，贵阳 550018; 2.贵州师范学院数学与计算机科学学院，贵州，贵阳 550001)

论Sylow 2-子群是Q8的8p3阶群的构造

陈松良1，蒋启燕2

(1.贵州师范学院数学与计算机科学学院，贵州，贵阳 550018; 2.贵州师范学院数学与计算机科学学院，贵州，贵阳 550001)

设p为奇素数(p≠3，7)，G是Sylow 2-子群为8阶四元数群Q8的8p3阶群，那么G恰有23个彼此不同构的类型。

有限群;同构分类;群的构造

设p是奇素数(p≠3，7)，文献［1］确定了Sylow 2-子群为交换群的8p3阶群的构造.本文将确定Sylow 2-子群为8阶四元数群Q8的8p3阶群的全部构造。我们有下面的定理:

定理1如果G是Sylow 2-子群为8阶四元数群Q8的8p3阶群，其中p是一个奇素数(p≠3，7)，那么G恰有23个彼此不同构的类型。

为了给出定理1的证明，在本文中，总假定p是奇素数(p≠3，7)，G是8p3阶群，其Sylow 2-子群为8阶四元数群Q8。由Sylow定理易知，G的Sylowp-子群是正规子群，从而G是P与Q8的半直积。为叙述方便，我们用|G|，|g|分别表示群G和元素g的阶，且对元素g，h，记gh=h－1gh.由文献［2］可知，8阶四元数群的构造为Q8=〈x，y||x|= 4，x2=y2，xy=x－1〉，由文献［3］知p3阶群有5种不同构的类型:循环群P1=〈a〉，其中|a|=p3;型为(p2，p)的交换群P2=〈a〉×〈b〉，其中|a|=p2，|b|=p;初等交换群P3=〈a〉×〈b〉×〈c〉，其中|a|= |b|=|c|=p;指数是p2的非交换群P4=〈a，b〉，其中|a|=p2，|b|=p，ab=a1+p;指数是p的非交换群P5=〈a，b，c〉，其中|a|=|b|=|c|=p，［a，b］=c，［a，c］=［b，c］=1。由于定理的证明较长，我们分为5个引理来描述，而且为了简化记号，我们将Q8简记为Q。

引理2设p是奇素数(p≠3，7)，G的Sylow 2-子群为Q而Sylowp-子群为循环群P1，那么G恰有2个彼此不同构的类型。

证 因为P1的自同构群Aut(P1)是阶为p2(p－1)的循环群，而Q/CQ(P1)同构于Aut(P1)的一个子群［4］，所以Q/CQ(P1)是循环群。但Q的循环商群只有单位群和2阶循环群，所以CQ(P1)=Q，或者CQ(P1)是Q的4阶循环子群。如果CQ(P1) =Q，则G是P1与Q的直积;如果CQ(P1)是Q的4阶循环子群，则不妨设CQ(P1)=〈x〉，从而y诱导P1的一个2阶自同构，于是G有如下的构造:

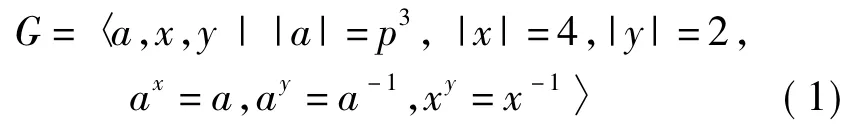
引理2得证。

引理3设p是奇素数(p≠3，7)，G的Sylow 2-子群为Q而Sylowp-子群为型为(p2，p)的交换群P2，那么G恰有5个彼此不同构的类型。

证因为P2的Frattini子群Φ(P2)=＜ap＞是p阶群，而 Φ(P2)charP2，P2◁G，于是Φ(P2)◁G。又不难证明〈ap，b〉是P2的唯一的p2阶初等交换子群，从而它是P2的特征子群，于是它又必是G的正规子群。由此可见，G必是超可解群。

由于〈ap〉及〈ap，b〉均为G的正规子群，从而都是Q-不变的.由［5］之定理8.1.2知〈ap〉在〈ap，b〉中有Q-不变的补子群，不失普遍性，可设〈b〉是Q-不变的。于是〈ap，b〉/〈ap〉是Q-不变的p2阶初等交换p-群〈a，b〉/〈ap〉的Q-不变子群，因此再由［5］之定理8.1.2知，〈ap，b〉/〈ap〉在〈a，b〉/〈ap〉中有Q-不变的p阶补子群〈aibj〉/〈ap〉，其中0＜i＜p2，0≤j≤p－1，且(i，p)=1，从而〈aibj〉是Q-不变的，但〈a，b〉=〈aibj，b〉，所以不妨设〈a〉也是Q-不变的.由此得Q/CQ(a)，Q/CQ(b)分别同构于Aut(〈a〉)与 Aut(〈b〉)的某个子群［4］.又 Aut (〈a〉)与Aut(〈b〉)都是循环群，所以CQ(a)与CQ(b)只能是Q或Q的4阶循环子群。

1)当CQ(a)=CQ(b)=Q时，显然G是P2与Q的直积。

2)当CQ(a)=Q，CQ(b)=〈x〉时，G有如下构造:

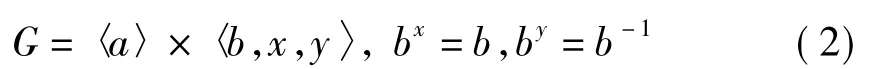
3)当CQ(a)=〈x〉，CQ(b)=Q时，G有如下构造:

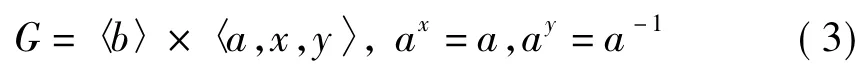
4)当CQ(a)=〈x〉，CQ(b)=〈y〉时，G有如下构造:

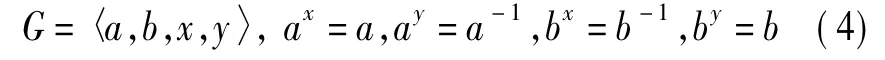
5)当CQ(a)=CQ(b)=〈x〉时，G有如下构造:

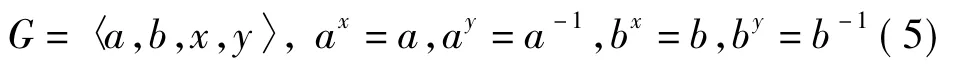
由于a，b在P2中是不对称的，因此上面得到的G的构造是互不同构的。证毕。

引理4设p是奇素数(p≠3，7)，G的Sylow 2-子群为Q而Sylowp-子群为p3阶初等交换群P3，那么G恰有9个彼此不同构的类型。

证因为Q在P3上的作用是互素的，所以由［6］之定理8.4.2，有P3=CP3(Q)×［P3，Q］。

1)当［P3，Q］=1时，G是P3与Q的直积。

2)当［P3，Q］是P3的p阶子群时，不妨设［P3，Q］=〈a〉，则CQ(a)为4阶循环子群，因此G有如下构造:

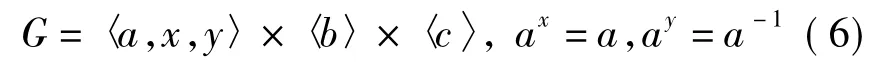
3)当［P3，Q］是P3的p2阶子群时，不妨设［P3，Q］=〈a，b〉.若G是超可解群，则不妨设〈a〉，〈b〉都是Q-不变的，于是CQ(a)与CQ(b)均为4阶循环子群.注意到a，b在P3中是对称的，因此这时G有如下几种不同构的类型:

3.1)当CQ(a)=CQ(b)=〈x〉时，G有如下构造:

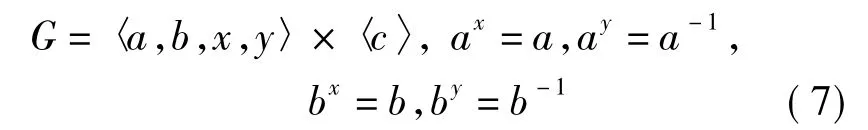
3.2)当CQ(a)=〈x〉，CQ(b)=〈y〉时，G有如下构造:

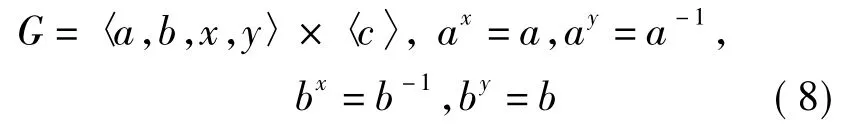
3.3)若G不是超可解群，则Q必忠实作用在〈a，b〉上。否则Q/CQ(P)是交换群，而〈a，b〉是Q-不可分解的，所以由［6］之定理8.3.3可知，Q/CQ(P)只能是2阶循环群，但2阶循环群在〈a，b〉上的作用是可分解的，于是G是超可解群，矛盾。显然Q的中心〈x2〉包含在GL(2，p)的Sylow 2-子群的中心中，于是x2是GL(2，p)的负单位元，所以x在〈a，b〉上的最小多项式必是λ2+1。不妨取，则由xy=x－1与y2=x2可得，，其中μ2+ν2≡－1(modp)。由数论知识可知，当p≡1(mod 4)时，μ2≡－1(modp)有解，从而μ2+ν2≡－1(modp)有解;当p≡3(mod 4)时，设k是模p的最小正二次非剩余，则k＞1且k－1与－k都是模p的二次剩余，即μ2≡k－1(modp)与ν2≡－k(modp)都有解，从而μ2+ν2≡－1 (modp)有解.由μ2+ν2≡－1(modp)的一组解μ，ν，可得G的一种构造:

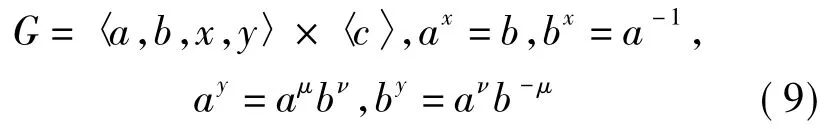
对于任何α，β，若α2+β2≡－1(modp)，我们证明存在整数k，l，m，n，使得当a1=akbl，b1=ambn，有，其中k n－lm≠0(modp)。从而，对于μ2+ν2≡－1(modp)的任何一组解，我们得到的G的构造均与(9)同构。

事实上，不妨设μ，ν≠±α，±β(modp)，则不难证明μα+νβ≠0(modp)。由得k≡n(modp)，l+m≡0(modp)，再由得

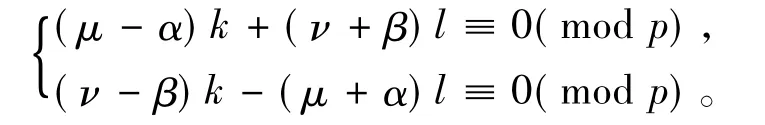
这个关于k，l的同余方程组有非零解(因为其系数行列式模p同余于0)，于是只需证明k2+l2≠0(modp)即可.因为这个同余方程组两边平方，得

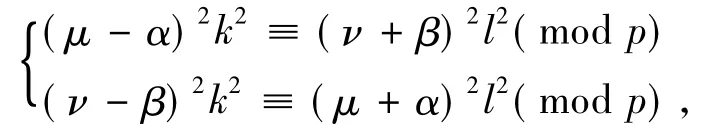
此二式两边分别相加得，

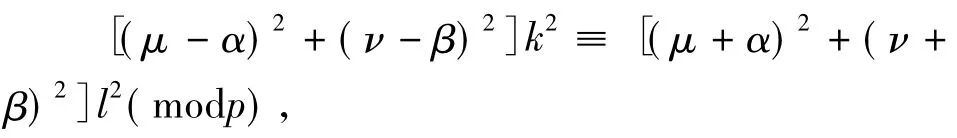
又μ2+ν2≡α2+β2≡－1(modp)，所以上式可化简为

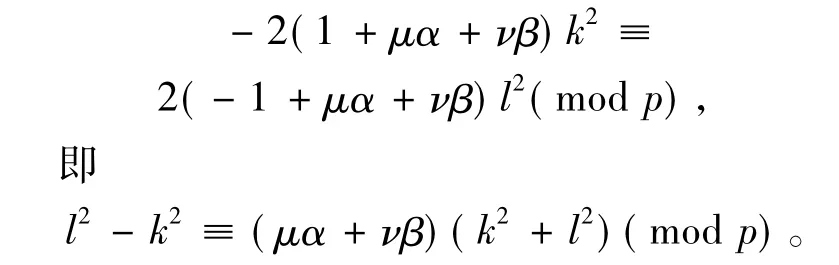
如果k2+l2≡0(modp)，则由上式得k2≡l2(modp)，再由上式得(μα+νβ)k2=0(modp)，从而k≡l≡0(modp)，这与k，l是同余方程组的非零解矛盾。

4)当［P3，Q］是P3的p3阶子群，即［P3，Q］=P3时，若G是超可解群，则不妨设〈a〉，〈b〉，〈c〉都是Q-不变的，于是CQ(a)，CQ(b)与CQ(c)均为4阶循环子群。注意到a，b，c在P3中是对称的，因此这时G有如下几种不同构的类型:

4.1)当CQ(a)=CQ(b)=CQ(c)=〈x〉时，G有如下构造:

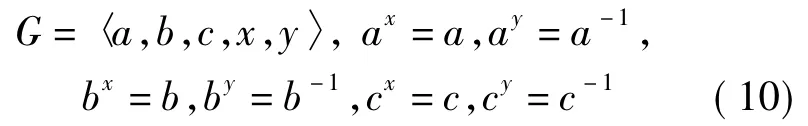
4.2)CQ(a)=〈y〉，CQ(b)=CQ(c)=〈x〉时，G有如下构造:

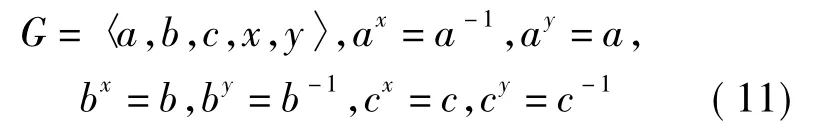
4.3)CQ(a)=〈x〉，CQ(b)=〈y〉，CQ(c)=〈x y〉时，G有如下构造:

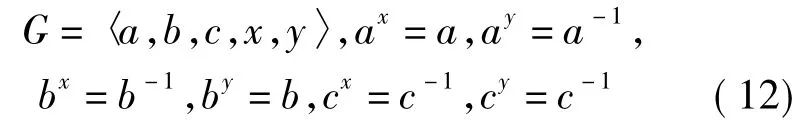
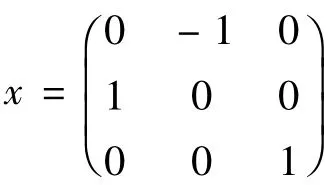
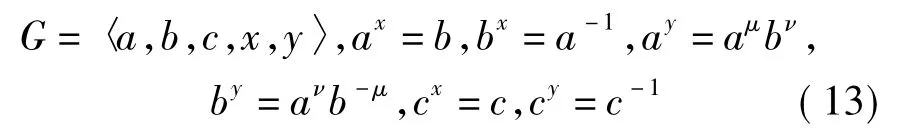
对于μ2+ν2≡－1(modp)的每一组值μ，ν，类似于3.3)，不难证明所得G的构造必与(13)同构.注意在(13)中，y的特征多项式是(λ+1)(λ2+ 1)，而x，y在Q中的地位是相同的，因此这种类型的构造只有(13)一种。引理4得证。

引理5设p是奇素数(p≠3，7)，G的Sylow 2-子群为Q而Sylowp-子群为指数是p2的p3阶非交换群P4，那么G恰有2个彼此不同构的类型。

证因为P4的中心C(P4)=〈ap〉是p阶群，而C(P4)charP4，P4◁G，于是C(P4)◁G。又不难证明〈ap，b〉是P4的唯一的p2阶初等交换子群，从而它是P4的特征子群，于是它又必是G的正规子群。由此可见，G必是超可解群。

由于〈ap〉及〈ap，b〉均为G的正规子群，从而都是Q-不变的。由［5］之定理8.1.2知〈ap〉在〈ap，b〉中有Q-不变的补子群，不失普遍性，可设〈b〉是Q-不变的。又〈ap，b〉/〈ap〉是Q-不变的p2阶初等交换p-群〈a，b〉/〈ap〉的Q-不变子群，因此再由［5］之定理8.1.2知，〈ap，b〉/〈ap〉在〈a，b〉/〈ap〉中有Q-不变的p阶补子群〈aibj〉/〈ap〉，其中0＜i＜p2，0≤j≤p－1，且(i，p)=1，从而〈aibj〉是Q-不变的，但〈a，b〉=〈aibj，b〉，所以不妨设〈a〉也是Q-不变的。由此得Q/CQ(a)，Q/CQ(b)分别同构于Aut(〈a〉)与Aut(〈b〉)的某个子群。又Aut(〈a〉)与Aut(〈b〉)都是循环群，所以CQ(a)与CQ(b)只能是Q或Q的4阶循环子群。

1)当CQ(a)=CQ(b)=Q时，显然G是P4与Q的直积。

2)当CQ(a)=〈x〉时，必有ax=a，ay=a－1。将x，y分别作用在［a，b］=ap的两边得bx=by=b，于是CQ(b)=Q，故G有如下构造:

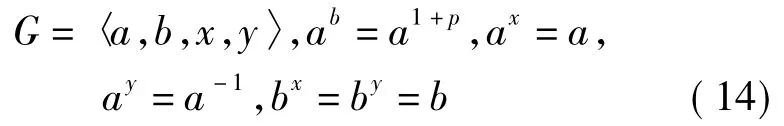
引理5证毕。

引理6设p是奇素数(p≠3，7)，G的Sylow 2-子群为Q而Sylowp-子群为指数是p的p3阶非交换群P5，那么G恰有5个彼此不同构的类型。

证因为C(P5)=〈c〉，而C(P5)charP5，所以〈c〉是G的正规子群，从而P5/〈c〉是Q-不变的.如果Q在P5上的作用是平凡的，则G是P5与Q的直积.如果Q在P5上的作用是非平凡的，且G是超可解的，那么不妨设〈a〉，〈b〉都是Q-不变的，于是CQ(a)与CQ(b)中至少有一个是4阶循环子群。注意到a，b在P5中是对称的，因此这时G有如下几种不同构的类型:

1)当CQ(a)=〈x〉，CQ(b)=Q时，将x，y分别作用在［a，b］=c的两边得cx=c，cy=c－1，于是G有如下构造:

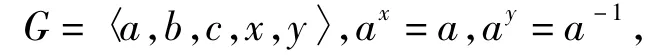
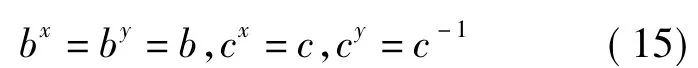
2)当CQ(a)=CQ(b)=〈x〉时，将x，y分别作用在［a，b］=c的两边得cx=cy=c，于是G有如下构造:

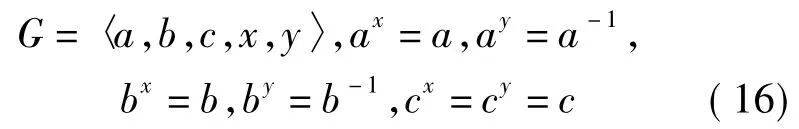
3)当CQ(a)=〈x〉，CQ(b)=〈y〉时，G有如下构造:

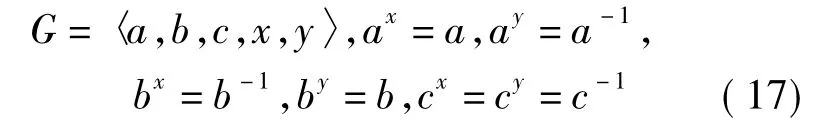
4)如果Q在P5上的作用是非平凡的，且G不是超可解的，那么P5/〈c〉是Q-不可分解的.这时类似于引理4中3.3)的讨论，可得G的如下构造:

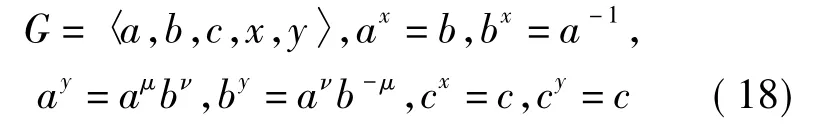
其中μ2+ν2≡－1(modp)。引理6证毕。

由引理2～6知，定理1成立。

［1］蔡 琼.23p3阶群的构造［J］.数学杂志，2005，25 (4):449-452.

［2］徐明曜.有限群导引(上册)［M］.北京:科学出版社，1999:25.

［3］张远达.有限群构造［M］.北京:科学出版社，1982: 467.

［4］［德］Huppert B.有限群论(第一卷第一分册)［M］.姜 豪，俞曙霞译.福州:福建人民出版社，1992:24.

［5］Robinson Q J S.A course in the theory of groups［M］.Springer-Verlag，New York，Heidelberg，Berlin，1982: 209.

［6］Kurzweil H，Stellmacher B.The Theory of Finite Groups［M］.Springer-Verlag，New York，Inc.2004:192-198.

On the complete classification of groups of order 8p3with Sylow 2-subgroupsQ8

CHEN Song-liang1，JIANG Qi-yan2
(1.School of Mathematics and Computer Science，Guizhou Normal College，Guiyang，550018; 2.School of Mathematics and Computer Science，Guizhou Normal College，Guiyang，550001)

Let p be an odd prime and G be groups of order 8p3with Sylow 2-subgroupQ8.In this paper，it is discussed that the isomorphic classification ofG，and their structures are completely determined.We have showed thatGhas 23 nonisomorphic structures.

finite group;isomorphic classification;structure of group

O152.1

：A

：1004-4329(2015)01-016-04

2014-10-11

贵州师范学院2013年重点支持学科，贵州省教育厅教改重点项目(黔教高发［2013］446号)资助。

陈松良(1964－)，男，博士，教授。研究方向：群论。