综合利用测井数据求取升平油田x区块储层参数
李全厚,王鹏丽,角远东,唐嘉琦
(1. 东北石油大学,黑龙江 大庆 163318; 2. 大庆钻探工程公司钻井三公司,黑龙江 大庆 163000;3. 大庆油田有限责任公司井下作业分公司,黑龙江 大庆 163000)
综合利用测井数据求取升平油田x区块储层参数
李全厚1,王鹏丽1,角远东2,唐嘉琦3
(1. 东北石油大学,黑龙江 大庆 163318; 2. 大庆钻探工程公司钻井三公司,黑龙江 大庆 163000;3. 大庆油田有限责任公司井下作业分公司,黑龙江 大庆 163000)
为做好储层评价工作,首先要认识现有测井饱和度的解释模型的现状,在参阅国内外有关文献的前提下,根据各种模型建立的背景,将饱和度解释模型分为经典Archie公式和考虑了泥质影响的印度尼西亚方程和Simandoux饱和度解释模型等等。除基本的Archie模型以外,这两种方程也有多种解释模型。每种方程都有其历史背景,基于升平地区的地质情况选择适宜该地区的解释模型。提高了该地区计算饱和度的符合率。
饱和度模型;电阻率;泥质;油气层
随着勘探开发的进一步进行,升平地区的测井解释工作也发现诸多问题,储层含泥量逐渐上升,岩石性质变得复杂,有效储层得识别也显得困难;油气水关系混乱复杂,油气水界限不清楚等[1]。能够准确计算出储层参数尤为重要,在经典的Archie模型提出后,经过几十年的发展,提出了各种各样的的饱和度模型,这些模型也都分别在一定情况下提高了该区的测井油气水层的解释符合率[2]。本文将从测井曲线分析、流体测井的响应特征等方面开展升平地区测井解释方法研究,力图增强测井对升平地区储层和油气水层识别能力,提高本区带测井综合解释的符合率,为下一步的勘探开发提供最基础的科学解释。
1 研究区地质概况
升平油田处于松辽盆地北部的中央坳陷区的三肇凹陷内,升平油田的主要生油层位为葡萄花油层,其储集层岩性主要是泥质砂岩[3]。升平油田主要为北东-南西走向的一个鼻状构造,并且沿着走向由北东方向向南西方向逐渐倾没。葡萄花油层的地层厚度大约为50 m左右,其顶部的埋藏深度约为1 420~1 550 m。该油层组的沉积砂体主要属于三角洲分流平原相以及内前缘相。
2 储层参数的求取
选取适宜升平地区的方法求取储层参数,以便进一步对储层进行评价。
2.1 泥质含量计算方法
计算储层泥质含量是下一步计算储层参数,评价储层参数的基础。储层的泥质含量反映着储层的岩性,同时,它还与储层的主要评价参数如有效孔隙度、渗透率、含水饱和度以及束缚水饱和度等有着密切的联系。所以储层泥质含量的计算精度也在一定程度上决定着储层参数的计算精度[4]。通常来说,各种方法计算的储层泥质含量与储层实际的泥质含量相比偏高。所以在实际计算过程中选择多种计算泥质含量的方法,然后选取几种方法计算出的最小泥质含量为最终得到的泥质含量。
2.1.1 自然伽马法
储层中的泥质含量越高,泥质吸附的放射性越强,导致自然伽马测井值增大[5],因此,可以利用自然伽马法确定地层的泥质含量(Vsh),其公式如下:
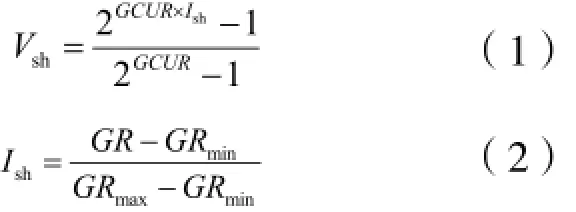
式中: GR、GRmax、GRmin—目的层自然伽马值、自然伽马最大值、自然伽马最小值,API;GCUR—系数。
2.1.2 自然电位法
自然电位测井在泥岩处给出了基线值,自然电位测井曲线在渗透层出现明显的负异常,异常值的幅度大小受储层泥质含量的影响[6]。储层泥质含量越高,则自然电位异常值幅度越小。所以可以用自然电位法来计算储层泥质含量。其方法如下:
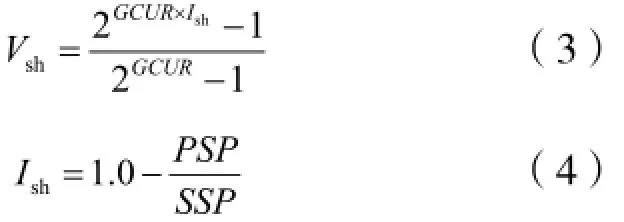
式中:
PSP —假静自然电位值,PSP = SP- SPsh,mV;
SSP —静自然电位值,SSP = SPsd- SPsh,mV;
SP、SPsd、SPsh—以某一基线为准,对泥质岩石、纯岩石和纯泥岩读出的自然电位值,mV;
GCUR —系数。
2.2 地层总孔隙度计算方法
2.2.1 声波时差法计算地层总孔隙度

式中:Δt、Δtmt、Δtf—分别为地层、干骨架、水时差,微秒/英尺。Δ tmt取54 μs/英尺。
2.2.2 中子-密度测井组合法计算地层总孔隙度

式中: ϕN、ϕD—分别为目的层的中子和密度孔隙度。
2.3 地层有效孔隙度计算方法
2.3.1 声波时差法计算有效孔隙度

式中: Δt、Δtma、Δtsh—分别是地层、骨架、泥质时差,μs/英尺;
Vsh—泥质含量,小数。
2.3.2 中子-密度组合法计算有效孔隙度

式中:
Vsh— 泥质含量;
ϕN、ϕNsh—目的层和泥质的中子孔隙度;
ϕD、ϕDsh—目的层和泥质的密度孔隙度。
2.4 地层含水饱和度计算方法
2.4.1 Archie 公式
Archie建立适用于纯砂岩油气层的岩石含水饱和度公式。即:
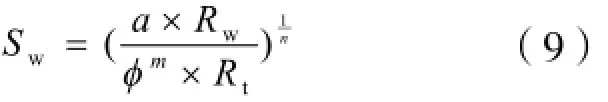
式中:
Sw—含水饱和度;
Rw—孔隙水电阻率;
Rt—岩石的电阻率;
ϕ —岩石孔隙度;
a,b,m,n —岩石特性参数。
表1和图1为Archie公式得到的含水饱和度值、与原试油资料的对比表、以及对比图。
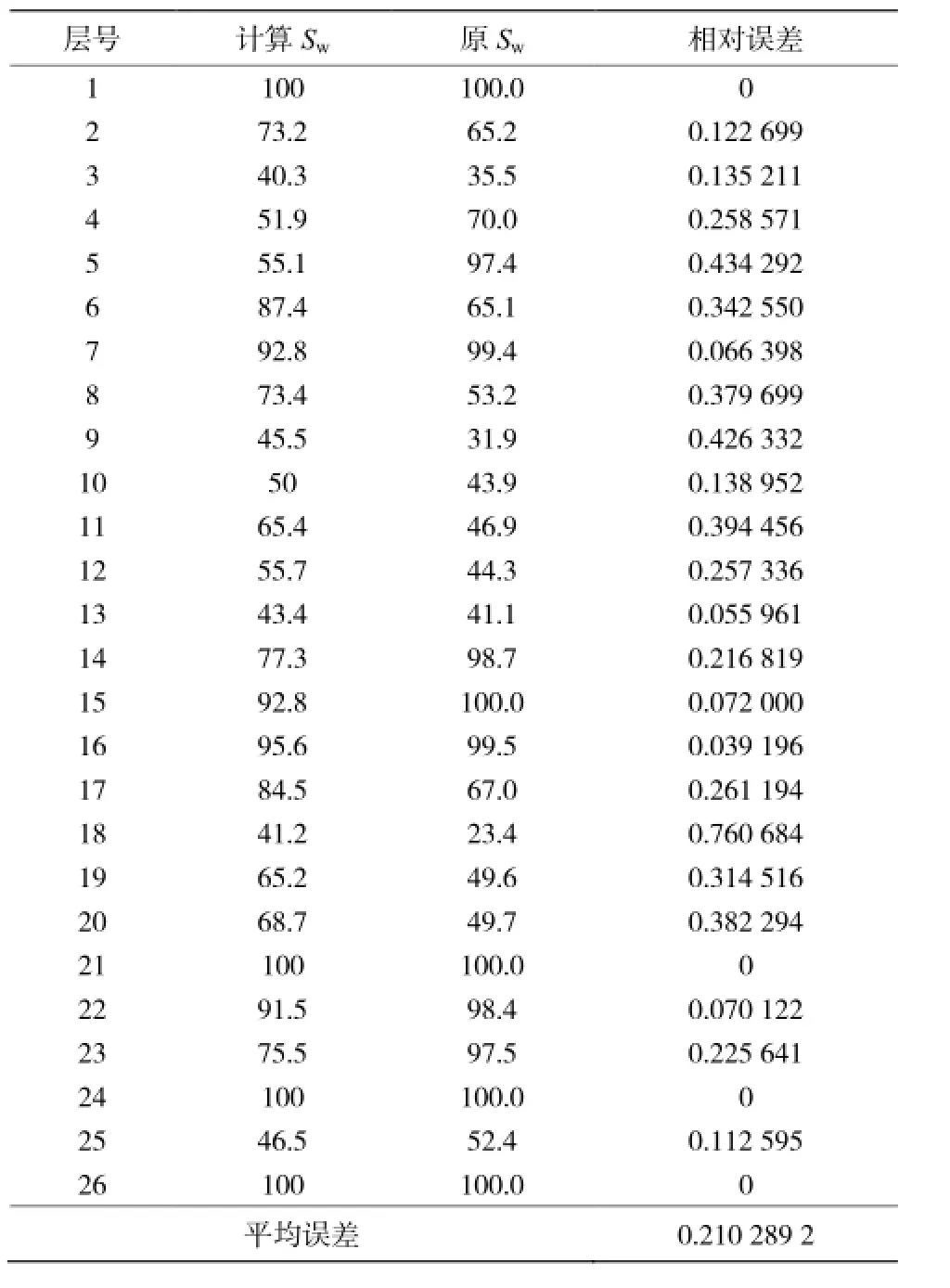
表 1 Archie公式计算得到含水饱和度相对误差Table 1 Relative error of water saturation by Archie formula

图1 阿尔奇公式计算值与试油结果对比图Fig.1 Comparison of results by Archie formula and test oil results
2.4.2 Simandoux方程
由于升平油田的泥质含量较高,原有的阿尔奇公式显然已经不再适用该地区,所以选择考虑泥质含量影响的Simandoux方程。
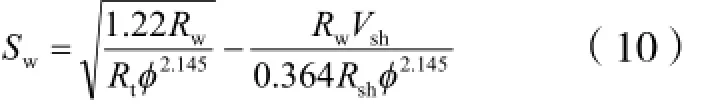
式中: Rt—地层的真电阻率;Rsh—泥岩电阻率。
2.5 改进的Simandoux方程
Simandoux公式计算含水饱和度与试油结果得出的含水饱和度仍有很大误差,利用C++拟和出新的Simandoux公式。
Simandoux修正后的公式如下:
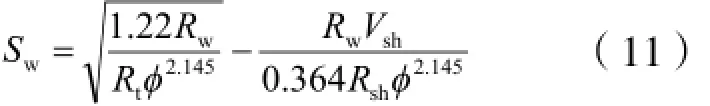
3 效果分析
修正的Simandoux公式得到的含水饱和度值、与原试油资料的对比表2、以及对比图2。

图2 修正的Simandoux公式计算值与试油结果对比图Fig.2 Modified Simandoux formula calculation value and test oil results
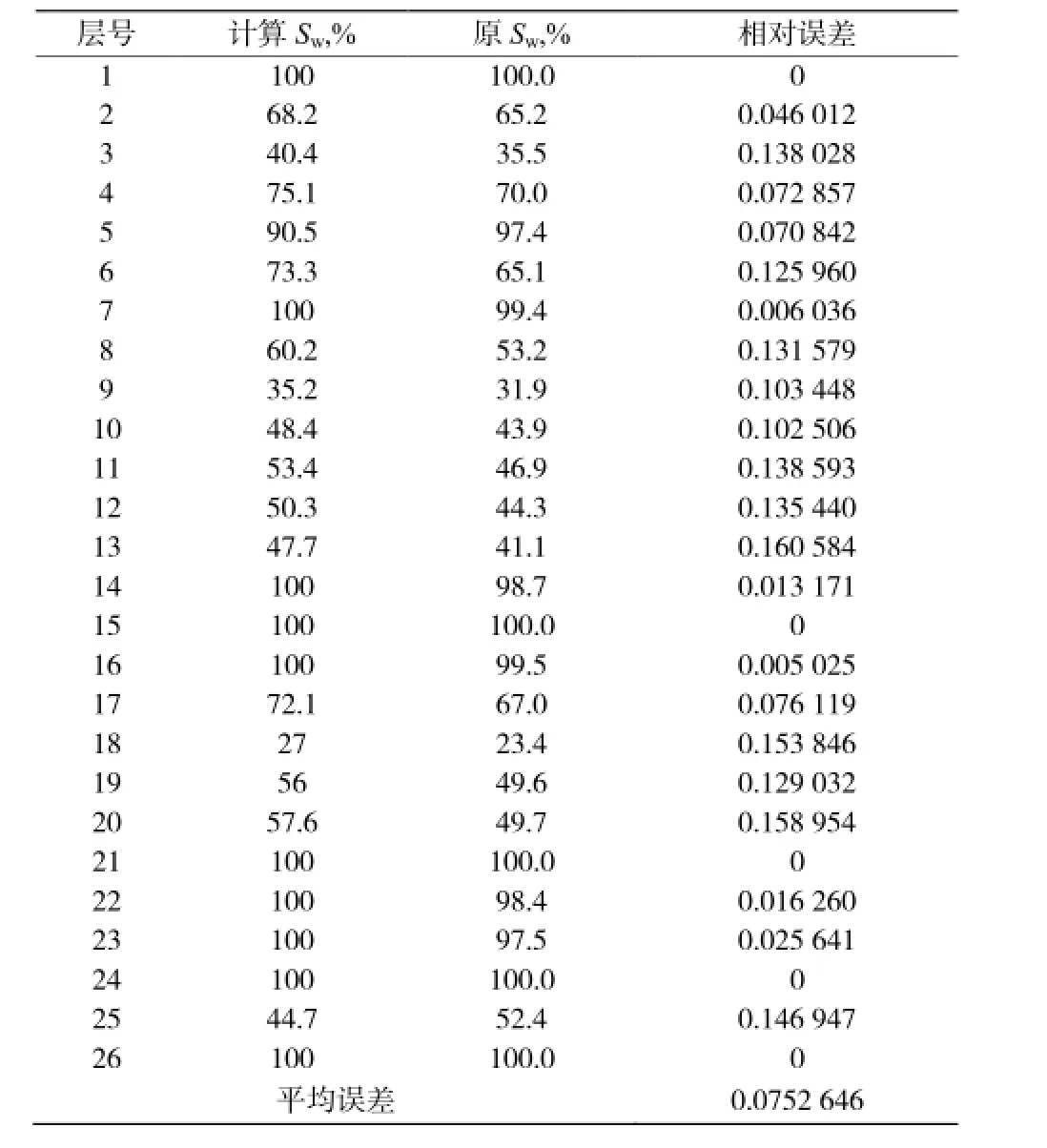
表2 修正的Simandoux公式计算值与试油结果对比表Table 2 Modified Simandoux formula calculation value and test oil results
4 结束语
本论文通过升平油田井曲线和相关数据统计,列举了几种计算含水饱和度的方法,不同方法适用于不同条件,各种方法有其简便的合理适用条件。
通过对井资料进一步的分析研究,选择了Simandoux公式的变形计算含水饱和度,计算出的结果相差并不大,证明这种方法可行,可用于那种泥质含量高,地层水矿化度高的升平地区,利用这种思想算法更精确的确定井地下岩层的岩心确切含水饱和度,并且该方法相对于其他方法更适用于升平油田这种上下层段的参数相差不大的油田,因为参数相差太大的上下层如果用这种方法计算,其平均出来的结果其误差可能比较大,不能真实的反映地下岩心的含水饱和度。
从最终的结果来看,还是存在误差的,误差存在的原因有很多方面,泥质含量、孔隙度的求取等等,对于含水饱和度小的地方求取误差比较大,还需进一步的研究。由于还没有到过现场,现场的经验一点都没有,有时候选的经验公式、校正公式和变量不是很准确,这样就会给运行结果带来一些不必要的误差,还有就是对测井资料掌握的不是很好和完全,也会使结果的误差很大。
[1]荆万学,陈永吉. 浅探阿尔奇公式的物理学原型[J] . 测井技术,199 7 , 21 (4) :2892291.
[2]Simandoux P. Dielect ric measurement s of porous media :Application to measurement of water saturations , study of t hebehavior of argillaceous formations [J] . Revue de L’ Institut Franais du Pet role ,1963 ,18 (S1) : 1932215.
[3]潘和平, 樊政军. 新疆塔北地区低电阻油气层测井评价技术[M] .北京:中国地质大学出版社, 2000.
[4]莫修文. 低阻储层导电模型的建立和测井方法研究[D] . 长春: 长春科技大学,1998.
[5]李薇, 田中元, 闫伟林, 等. Y 油田低电阻率油层形成机理及RRS R 识别方法 [J] . 石油勘探与开发,2005 ,32 (1) :60262.
[6]朱家俊,耿斌,耿生臣, 等. 宏观导电机理下的泥质砂岩含水饱和度解释模型[J] . 石油勘探与开发,2003 ,30 (4) :75277.
Comprehensive Application of Well Logging Data in Obtaining Reservoir Parameters of X Area in Shengping Oilfield
LI Quan-hou1, WANG Peng-li1,JIAO Yuan-dong2,TANG Jia-qi3(1. Northeast Petroleum University, Heilongjiang Daqing 163318,China;
2. Daqing Drilling Company the Third Drilling Branch, Heilongjiang Daqing 163000,China;3. Daqing Oil Field Co.,Ltd. Downhole Operation Company, Heilongjiang Daqing 163000,China)
For the better reservoir evaluation, we must firstly understand the situation of logging interpretation model of saturation. According to various modeling backgrounds, the saturation interpretation models are divided into the classical Archie formula,Simandoux saturation interpretation model and Indonesia equation considering the effect of shale. Except for the basic Archie model, the other two equations have various interpretation models. Each equation has its historical background,so appropriate interpretation model for Shengping oilfield should be chosen based on geological conditions to improve the coincidence rate of saturation calculation of the area.
Saturation model;Electrical resistivity;Shale;Hydrocarbon reservior
TE 122
: A
: 1671-0460(2015)02-0340-03
2014-09-05
李全厚(1969-),男,黑龙江大庆人,高级工程师,副教授,1995年硕士毕业于大庆石油学院(现东北石油大学)矿场应用地球物理专业。E-mail:Liqh1@126.com。
王鹏丽(1989-),女,硕士学位,研究方向:地球探测与信息技术。E-mail:qingse819188820@163.com。
——高大庆作品欣赏

