L区块储层测井二次解释模型研究

张庆国，张 磊，庞文涛，王志远

（1. 东北石油大学地球科学学院， 黑龙江 大庆 163000； 2. 大庆油田有限责任公司录井公司， 黑龙江 大庆 163000；3. 新疆油田公司 石西油田作业区，新疆 克拉玛依 634000）

L区块储层测井二次解释模型研究

张庆国1，张 磊1，庞文涛2，王志远3

（1. 东北石油大学地球科学学院， 黑龙江 大庆 163000； 2. 大庆油田有限责任公司录井公司， 黑龙江 大庆 163000；3. 新疆油田公司 石西油田作业区，新疆 克拉玛依 634000）

测井资料的二次解释对重新进行储层评价具有十分重要的意义, 测井资料二次解释对于剩余油挖潜也具有指导意义，结合油田本油田的实际情况,二次测井解释的关键利用取心井分析化验、实验资料和试油试采资料,结合开发动态资料,建立了适合该区的储层参数测井解释模型,提高了储层参数的精度,为该区块进一步的勘探开发及精细注水指导奠定了基础。

测井资料；二次解释；储层参数

L区块油藏主要受构造控制，属于裂缝性中等渗透构造砂岩油藏。区块内断层多、断裂系统复杂、油藏埋深浅、油层多而薄且多分布在构造高点，物性差异大；水驱效果较差等地质特点, 此区块储层参数孔隙度为16%～30%之间, 渗透率为 （10～500）×10-3μm2之间, 平均泥质含量为7%；从上述参数可以看出此区块储层为中孔中渗透储层。我们应用岩心分析和实验资料、测井、试油、试采、生产开发动态等资料, 并结合该区中等孔隙度中等渗透率油层特征, 研究出适合于该区块的测井二次解释模型和油水层识别标准, 提高了测井一次解释精度和准确性。

1 测井资料预处理

储层的泥质含量和孔隙度是储层储集能力的显示, 储层渗透率是指示储层的渗透能力的主要指标参数, 储层岩性特征是确立油气水层电性差异大小的重要根据, 储层的含油性是测井油气水层评价与定量解释的重要指标, 储层参数的准确计算是建立测井二次解释模型的基础[1]。测井资料的预处理工作是储层参数测井二次解释的首要工作, 也是测井解释模型精确与否的关键的前提[2]。为了提高测井二次解释的精确性, 在测井解释前要对整个区块的测井曲线和岩心数据做必要的整理与处理；包括测井曲线的深度校正、测井曲线的编辑、测井曲线标准化和岩心深度归位等[3]；此区块的测井系列比较多测井曲线不统一，测井曲线标准化是此次测井二次解释最重要的一个环节。

1.1 标准化

本区块由于开采时间比较长，开发时测井系列差异比较大，存在以3700、JD581、5700 、多线型、小数控、大数控等多种测井系列，众多测井系列导致由于开发时间的原因测井曲线的类型也有很大的差别，测井分辨率及测井精度及测井曲线的类型都有很大的差别。需要对不同的测井系列、不同年代的测井曲线及不同的测井曲线类型进行标准化，为根据测井曲线细分层及测井精细解释模型的建立奠定坚实的基础。测井资料标准化方法很多，归纳起来大致可以分为定性和定量两大类。定性的主要是直方图法和均值校正法，定量主要是趋势面分析法。本次研究主要采用直方图法和趋势面分析法，同时采用直方图平移法和趋势面校正法相结合的方法[7]。校正后的声波时差值更符合本地区地质变化规律，有效降低了其他非地质因素给测井曲线在测量时带来的误差[4]。

2 测井解释模型的建立

2.1 岩性参数—泥质含量解释模型

一般情况下自然伽马测井对储层泥质含量有较好的测井响应。研究区块自然伽马测井放射性强度与储层泥质含量间有较好的相关性，因此，可以采用自然伽马曲线建立关系公式计算泥质含量，其计算公式如下：

泥质相对指数GSH为：

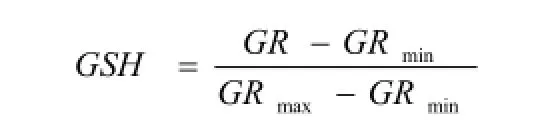
泥质含量Vsh为：

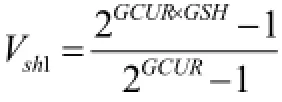
式中：GSH —用自然伽马曲线求取的泥质相对指数，无量纲；

Vsh—自然伽马曲线求取的储层泥质含量，%；

GRmax—某一井段纯泥岩自然伽马测井值，API；

GRmin—某一井段纯砂岩自然伽马测井值，API；

GR—某一井段自然伽马测井值，API；

GCUR—希尔奇指数，老地层取2。

2.2 物性参数—孔隙度解释模型

本区块研究首先以岩心分析的孔隙度数据为基础数据，根据岩心分析孔隙度与声波时差的较高相关性，声波时差做了标准化，使每个测井系列的声波时差时校正到符合本区块地质特征的范围，所以选择声波时差曲线建立孔隙度测井解释模型[5]。因此，使用声波时差与孔隙度进行线性回归(图1)。

考虑到研究区块泥质含量较高的特点，对使用声波时差求取有效孔隙度有比较大的影响，需要做泥质校正。得到对泥质含量进行校正后的孔隙度计算公式：Φ= 0.1098×Δt-9.4927-0.34×Vsh×100，通过对岩心实验得到的岩心孔隙度值分析与对比,岩心分析得到的孔隙度值与校正的孔隙度公式计算出的孔隙度值平均绝对误差为 1.7%,相对误差为6.8%符合本区块的解释标准要求。

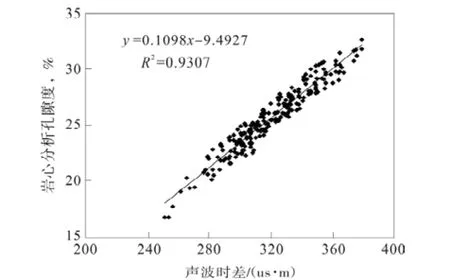
图1 孔隙度与声波时差交会图Fig.1 Porosity and slowness crossplots

2.3 物性参数—渗透率解释模型

渗透率是评价储层物性的重要参数；影响着渗透率计算的因素比较多, 因此如何准确计算渗透率是本次储层测井二次解释的关键；一般来说可以通过岩心分析的渗透率与测井曲线或测井曲线计算的参数（如孔隙度）直接建立统计关系[6]。通过对岩心实验分析得出的渗透率、孔隙度；还有结合分选粒度中值等资料进行分析和对比后，可知岩心分析孔隙度与岩心分析渗透率存在着较好的对数关系，故可以采用单独的孔隙度来建立渗透率测井解释模型。（如图2）得到的测井解释渗透率计算公式:K= 0.0002×e0.5103×Φ。经岩心分析得到的渗透率值分析，公式计算的渗透率值与岩心分析得到的渗透率值平均相对误差为10%。符合本区块的解释标准要求。

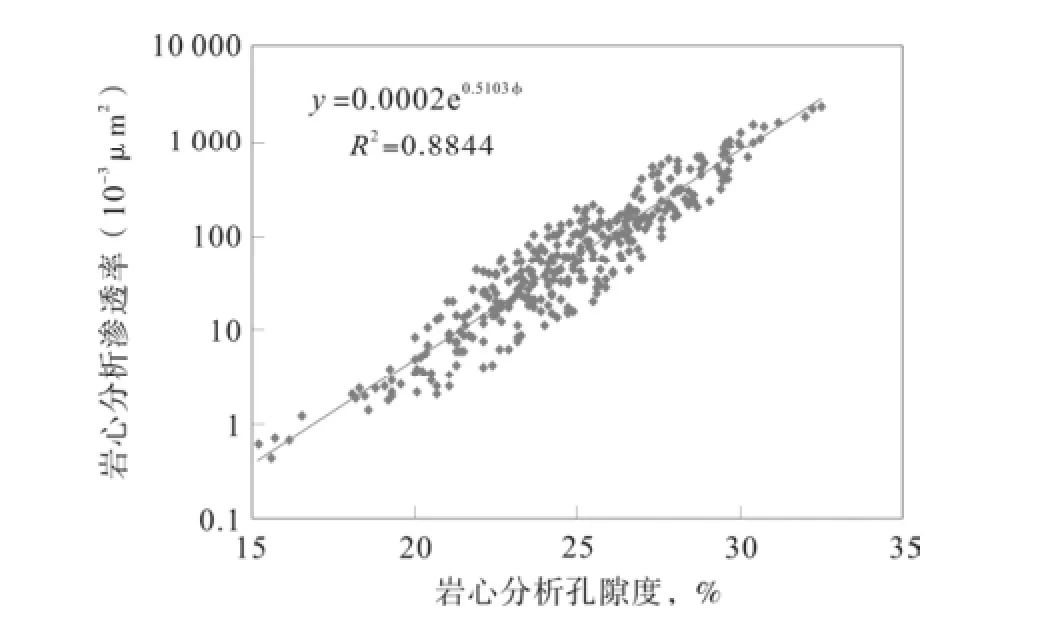
图2 孔隙度与渗透率交会图Fig.2 Porosity and permeability crossplot

2.4 含油性参数—含油饱和度解释模型

储层油层含油性的定量评价（含油饱和度）是储量计算及剩余油分析评价的基础，也是油水层判断的重要评价指标。储层的含油饱和度不仅与构造位置有关，还与储层的岩性和物性等多种因素影响相关联。常规测井解释经常利用阿尔奇公式来计算含水饱和度，储层含水饱和度反映了储层的岩性、物性、胶结情况等储层情况；根据阿尔奇公式要准确计算含水饱和度，首先应该进行岩电实验分析，确定岩性、孔隙有关的孔隙度、饱和度指数和胶结系数的值，再确定有效孔隙度、原状地层电阻率和地层水电阻率[7]。

经过岩电实验综合分析，确定本区块阿尔奇公式计算含水饱和度的岩电指数a, b, m, n的值。含水饱和度公式如下：

式中：

岩电参数—由岩电实验提供，a=1.1，m=1.41，b=1.12，n=1.68；

Rw—为地层水电阻率平均值（经检查井分析取1.2 Ω·m）；

Rt—为原状地层电阻率，可直接用深探测电阻率，Ω·m；

φ—为油层有效孔隙度，%。

因此，可以直接使用阿尔奇公式来求取含水饱和度进而求取含油饱和度。经过验证，此公式适用于地区。

3 油水层判别标准

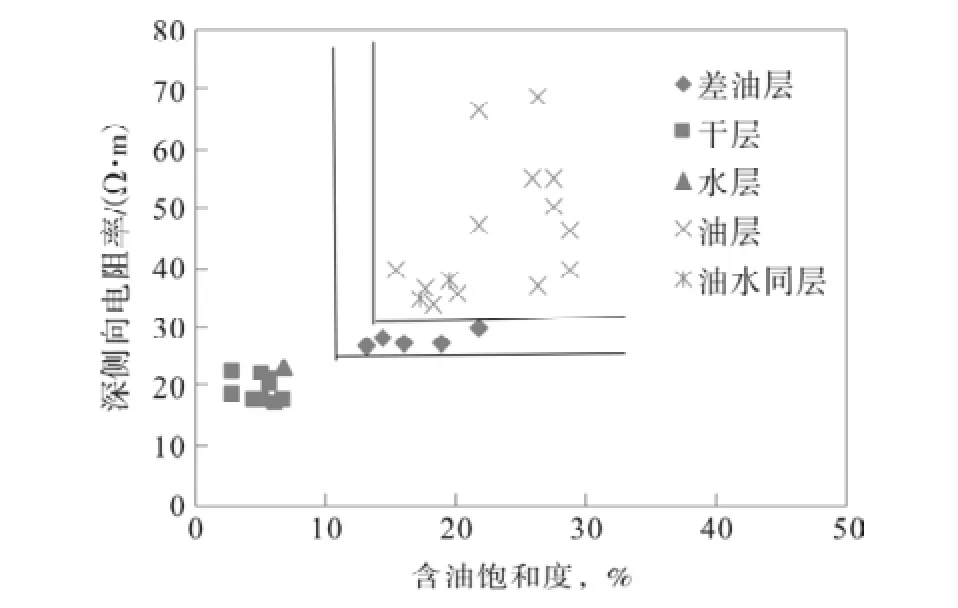
图3 深侧向电阻率与含油饱和度交会图Fig.3 Deep lateral resistivity and oil saturation crossplot

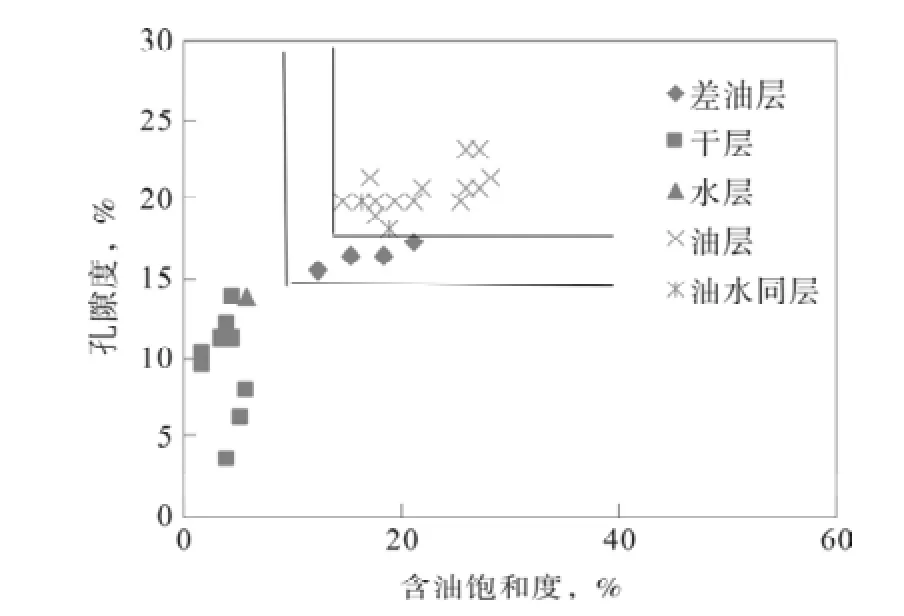
图4 孔隙度与含油饱和度交会图Fig.4 Porosity and oil saturation crossplot

根据本区块的试油资料和岩心分析化验资料,制作储层含油饱和度与深侧向电阻率交会图版（图3），储层含油饱和度与孔隙度交会图（图4), 根据此交会图版显示确定本区块油水层判别标准，确定油层与油水同层深侧向电阻率、孔隙度、储层含油饱和度的范围[8]：孔隙度值范围大于等于18% ,深侧向电阻率值大于等于26 Ω·m ,储层含油饱和度值范围大于等于22%;差油层深侧向电阻率、孔隙度、储层含油饱和度的范围：孔隙度值范围大于15%小于18%，深侧向电阻率值范围大于20 Ω·m小于26 Ω·m，储层含油饱和度大于19%小于22%；水层深侧向电阻率、孔隙度、储层含油饱和度的范围：孔隙度值范围小于15%,深侧向电阻率值范围小于 20 Ω·m ,储层含油饱和度值范围小于19%。

把本区块的井划分四个年代分析孔隙度（图5）和渗透率（图6）的变化规律，从图形中看出孔隙度值主要分布在16%～30%，占整体的85%，特征峰值为24%，平均值为21%；渗透率值主要分布在10×10-3～500×10-3μm2，占整体的80%，特征峰值为50×10-3μm2，平均值为230×10-3μm2。得出的结论是随着注水冲刷程度加深，孔隙度和渗透率有逐渐增大的趋势。本区块水淹比较严重随着水驱效果的增大，孔隙度和渗透率有变好的趋势。

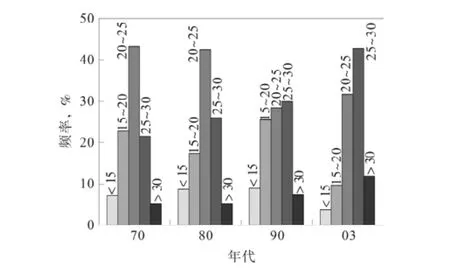
图5 孔隙度4个年代变化直方图Fig.5 Change of the porosity in four years

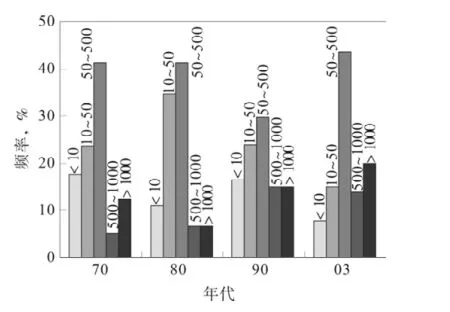
图6 渗透率4个年代变化直方图Fig.6 Change of the permeability in four years

4 结束语

利用此次建立的测井二次解释模型和经验公式,并且利用专业的测井评价软件Forward 2.71 测井解释平台, 处理了200 口井的静态资料。

将解释结果进行油水关系对比, 并用实际的试油, 试采资料与解释的油水层相互验证, 通过验证得知这次解释结果的符合率比原先的解释结果提高了5%,充分说明本次所建的测井解释模型符合油田所要达到的精度。基本上达到了预期的效果,并为油田下一步的勘探开发奠定了基础并且为精细注水提供了有利的理论依据。

［1］雍世和.测井数据处理与综合解释[M].东营:石油大学出版社, 1996.

［2］徐春华，范小秦，邓强．砂砾岩油藏已开发区测井二次解释方法及应用—以克拉玛依油田五3中区三叠系克下组油藏为例[J].地质学刊，2013(2)：193-198.

［3］孙鲁平，首 皓，李 平，张 颖.非均质储层测井二次解释——以辽河GS油田为例[J].石油天然气学报，2009,31(4):91-95.

［4］纪智，张庆国，孙德瑞. Z区块测井曲线的标准化方法[J].黑龙江科技大学学报（自然科学版）,2014(2):191-195.

［5］胡列侠，李剑, 侯瑞源，文东非均质储层测井二次解释模型研究[J].内蒙古石油化工，2008(12):90-91.

［6］杨映涛，陈恭洋，牛圈湖油田低孔特低渗油层测井二次解释[J].重庆科技大学学报（自然科技版），2007(2):7-9.

［7］宋瑶，苏妮娜，华吴平 .老君庙油田测井解释方法研究[J].测井技术,2012(6):596-598.

［8］刘延梅.中深层天然气储层“四性”关系研究及解释标准建立[D].中国石油大学（华东），2007.

Secondary Interpretation Model for L Block Reservoir Logging

ZHANG Qing-guo1，ZHANG Lei1，PANG Wen-tao2，WANG Zhi-yuan3
（1. Northeast Petroleum University, Heilongjiang Daqing 163000，China；2. Daqing Oilfield Limited Company Logging Branch, Heilongjiang Daqing 163000，China; 3. Xinjiang Oilfield Company Shixi Operation Area,Xinjiang Kelamayi 634000, China）

Secondary interpretation of logging data has a great significance for re-evaluation of reservoir, and has a guiding significance for remaining oil exploitation. Combined with the actual situation of the oil field, it’s pointed that key factors to affect the secondary interpretation are coring laboratory analysis, laboratory data and production test data. Combined with the development dynamic data, suitable logging interpretation model can be established to improve the accuracy of reservoir parameters, which will lay the foundation for further exploration and development of the blocks.

Logging data; Secondary interpretation; Reservoir parameters

TE 122

： A

： 1671-0460（2015）02-0268-03

2014-08-18

张庆国（1969-），男，黑龙江大庆人，副教授，博士学位，2007年毕业于中国石油大学(北京)矿物学、岩石学、矿床学专业，研究方向为石油综合地质和综合测井资料解释。E-mail：zhangqg@163.com。

张磊（1989-），男，研究方向为地球探测信息与技术。E-mail：zlcope@sina.com。