一种三项CD共轭梯度法及其全局收敛性

李 灿，汤玲霞

(红河学院数学学院，云南蒙自661199)

考虑无约束优化问题［1］

其中f:Rn→R是连续可微函数，▽f(x)表示函数的梯度.经典的共轭梯度法［2］求解问题(1)所产生的点列{xk}满足如下的迭代格式

其中αk表示由线性搜索确定的步长，dk表示第k次迭代的搜索方向且迭代格式如下

其中βk为参数.

2006年，Zhang等［3］对BFGS算法的搜索方向进行了深入分析，并与经典共轭梯度法的搜索方向进行了对比分析，由此提出了一种下降型PRP共轭梯度法，其搜索方向的迭代格式如下

1 算法

下面提出三项CD共轭梯度法，其搜索方向dk表示如下

其中

将 βk，ηk代入上式，便有 ▽f(xk)Τdk=－2‖▽f(xk)‖2.综上所述，

因此该搜索方向dk具有充分下降性.

在上面的基础上，我们提出求解(1)的一种三项CD共轭梯度法，其步骤如下:

步骤3.由强Wolfe型线性搜索

确定步长αk;

步骤4.令xk+1=xk+αkdk;

步骤5.由(4)确定dk+1，令k:=k+1，转步骤2.

2 算法的全局收敛性

本节证明三项CD共轭梯度法在下列假设下具有全局收敛性.

假设1

(b)在Ε的领域Β内，目标函数f连续可微有下界，且其梯度▽f是Lipschitz连续的，即存在常数L＞0，使得

引理1若假设1成立，点列{xk}由三项CD共轭梯度法产生，则

另一方面，由Lipschitz条件(7)有

则有‖▽f(xk+1)－▽f(xk)‖·‖dk‖≤Lαk‖dk‖2，于是

由(9)，(10)可得

即

进一步，综合强Wolfe线性搜索条件(6)和(11)有

上述不等式两边对k求和，并注意f(xk)有界，则有

从而

结合(5)，不难推出下面的引理:

引理2若假设1成立，点列{xk}由三项CD共轭梯度法产生，则

定理1若假设1成立，点列{xk}由三项CD共轭梯度法产生，则

证明 由搜索方向dk的迭代格式(4)有

将ηk代入，可以推出ηkyk－1的表达式

然后再将(15)代入(14)，进一步得到‖dk‖2的表达式

化简后

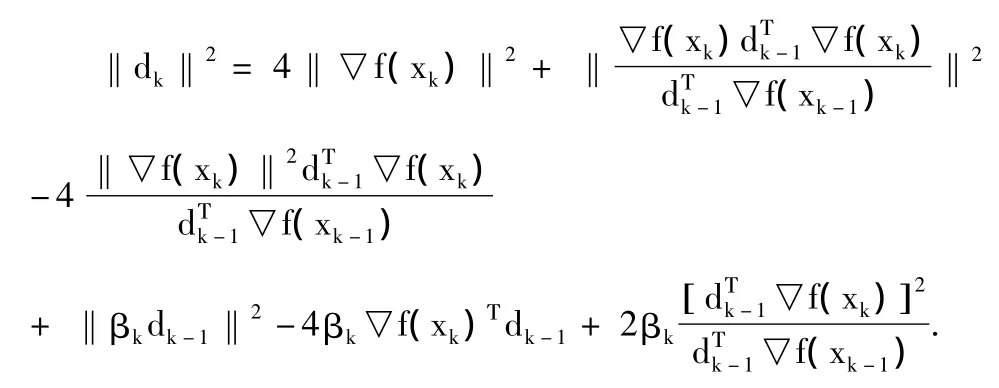
将βk代入，可以得到

即有

［1］陈宝林.最优化理论与算法［M］.北京:清华大学出版社，2004.

［2］李董辉，童小娇，万中.数值最优化［M］.北京:科学出版社，2005.

［3］Zhang L，Zhou W，Li D.A descent modified Polak－Ribiere－Polyak conjugate gradient method and its global convergence［J］.IMA Journal of Numerical Analysis，2006，(4):629－640.

［4］Andrei N.On three－term conjugate gradient algorithms for unconstrained optimization［J］.Applied Mathematics and Computation，2013，(11):6316－6327.

［5］Al－Bayati A Y，Sharif W H.A new three－term conjugate gradient method for unconstrained optimization［J］.Canadian Journal on Science and Engineering Mathematics，2010，(5):108－124.

［6］Narushima Y，Yabe H，Ford J A.A three－term conjugate gradient method with sufficient descent property for unconstrained optimization［J］.SIAM Journal on Optimization，2011，(1):212–230.

［7］Zhang L，Zhou W，Li D.Some descent three－term conjugate gradient methods and their global convergence［J］.Optimization Methods and Software，2007，(4):697–711.