整函数及其微分多项式权分担值

甘 媛

(福建船政交通职业学院公共教学部，福建福州350007)

1 相关知识

近年来，Lahiri与Banerjee引进了一种权分担的方法讨论了亚纯函数及微分多项式的唯一性问题，这种方法极大地改进了IM及CM思想.根据权分担思想，本文完整的讨论了(fn)(k)与(gn)(k)权分担1值问题，得到以下结果.

定理1.1:若f，g为两个非常数整函数，正整数n，k满足n ＞5k+7.如果(fn)(k)与(gn)(k)分担(1，0)，则f=c1ecz，g= c2e-cz或 者 f= tg;其 中 c，c1，c2，t 为 满 足(-1)k(c1c2)n(nc)2k=1及tn=1的常数.

定义 1.1:设 f，g(1，0)分担，z0为f的q重1- 值点，定义为f，g公共1-值点且p=q=1时的计数函数为f，g公共1-值点且p＞q时的计数函数;为f，g公共1-值点且p=q≥2时的精简计数函数;类似地有我们记为公共1-值点的精简计数函数，且满足p＞q=k，类似地有

2 主要引理及其证明

为证明定理我们需要以下引理.

引理 2.1［1］:若 f为非常数整函数，k 为正整数，c 为非零有限复常数，那么

其中N0(r，0;f(k+1))为f(k+1)的零点但不是f(f(k)-c)的零点的计数函数的密指量.

引理 2.2［1］:若 f为非常数整函数，两个亚纯函数 α1，α2满足，那么

引理2.3:若f为非常数整函数，为k正整数，那么

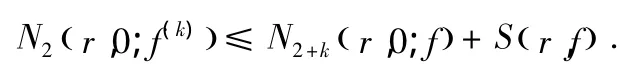
证明:由于 f为整函数及文献［2］，有 N(r，0;f(k))≤N(r，0;f)+S(r，f).

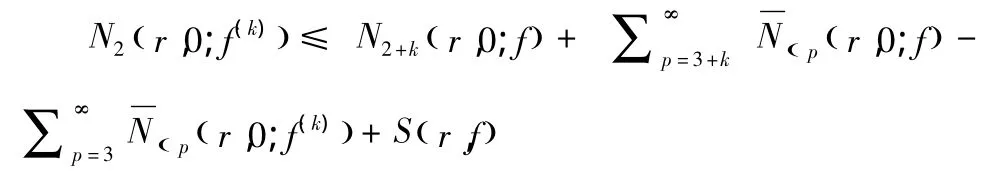
故引理2.3得证.

引理2.4［3］:若 f为非常数整函数，正整数 k ≥ 2.如果ff(k)≠0，那么 f=eaz+b，这里 a≠0，b为复常数.

引理 2.5［4］:如果两个非常数整函数 F，G 分担(1，0)且满足H≠0，那么

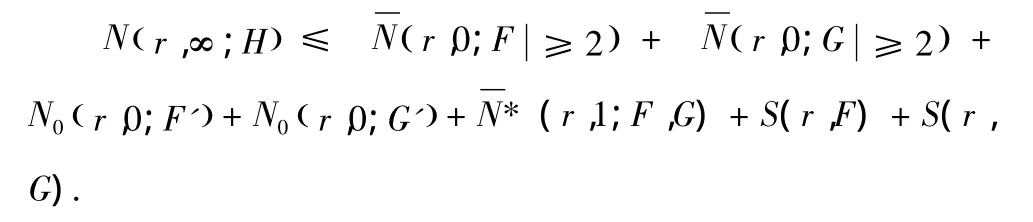
这里N0(r，0;F′)为F′的零点但又不是F(F-1)的零点的计数函数的精简密指量，类似地有N0(r，0;G′).

引理 2.6［5］:如果两个非常数整函数 F，G 分担(1，0)且满足H≠0，那么

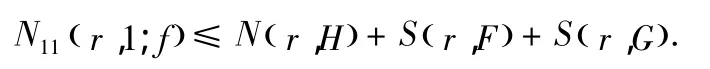
引理2.7:如果两个整函数分担，那么

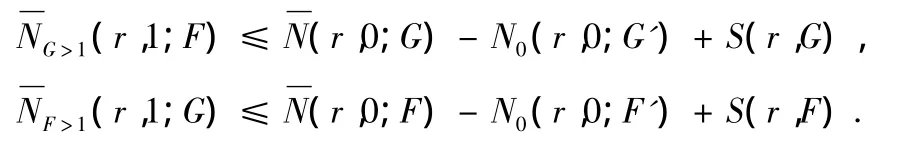
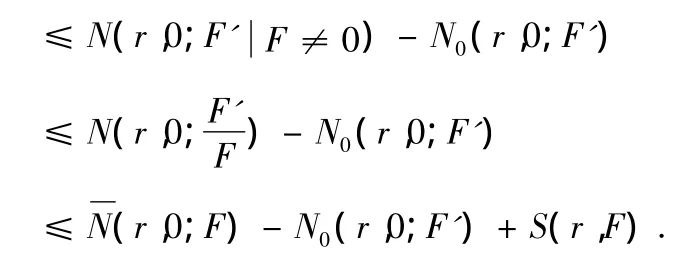
引理2.8:若两个非常数整函数分担，那么

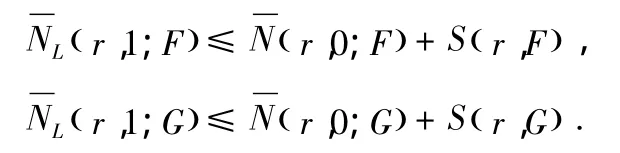
证明:由文献［5－8］知

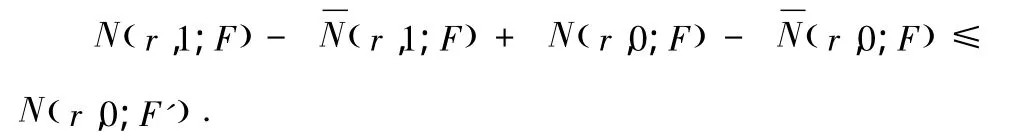
由 于 F，G 为 整 函 数，有 N(r，0;F′)≤ N(r，0;F)+S(r，F).

类似地可以得到引理中的第二个式子，这样引理2.8得证.

引理2.9:若f，g为两个非常数整函数，k为正整数，如果f(k)与g(k)分担(1，l)，若 l=0，

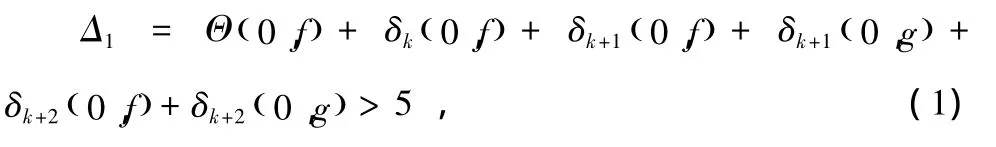
当l=0，于是F，G分担(1，0)，假设H≠0，那么得到

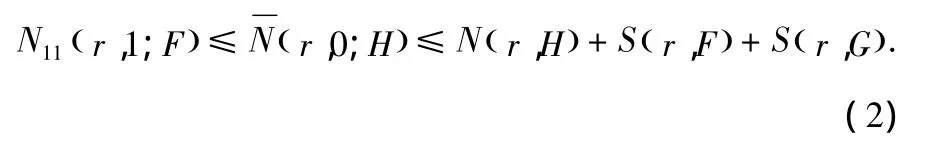
那么根据引理 2.5，2.6，2.7，2.8 及(2)式，有

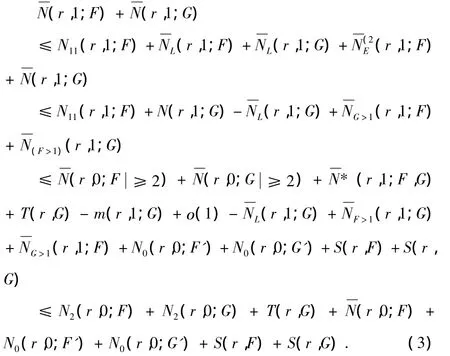
因为F=f(k)及G=g(k)，

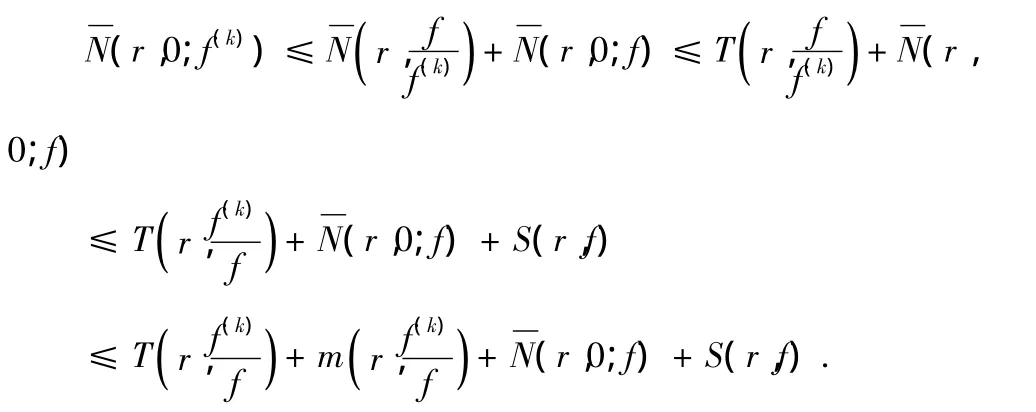
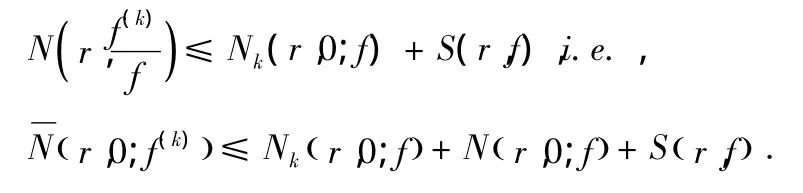
因此根据引理2.3，(3)式变为

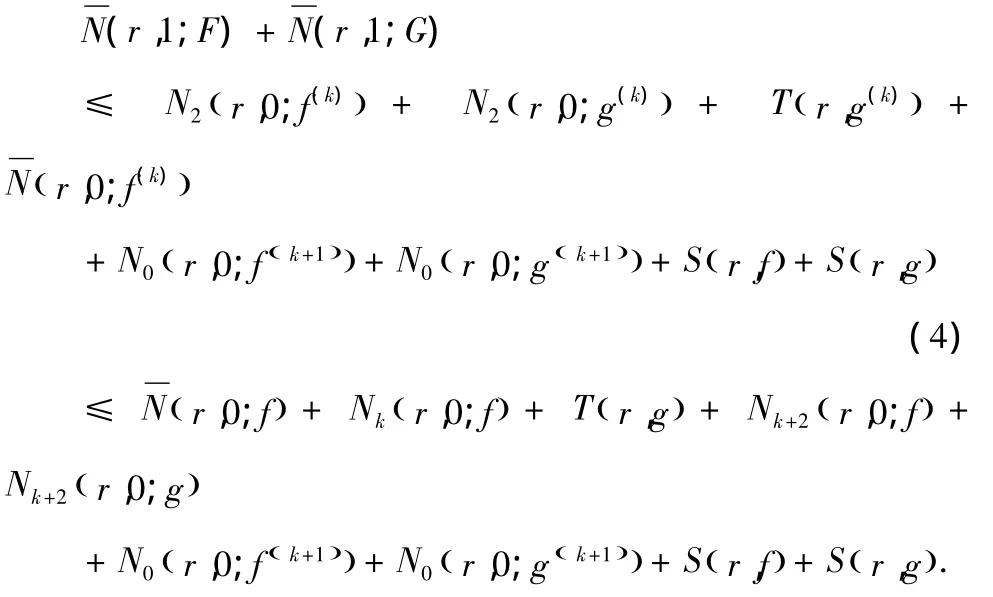
再根据引理 2.1，有

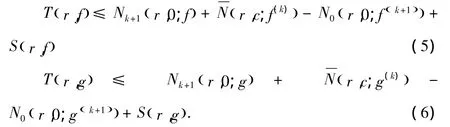
这样，由(2)—(6)，有

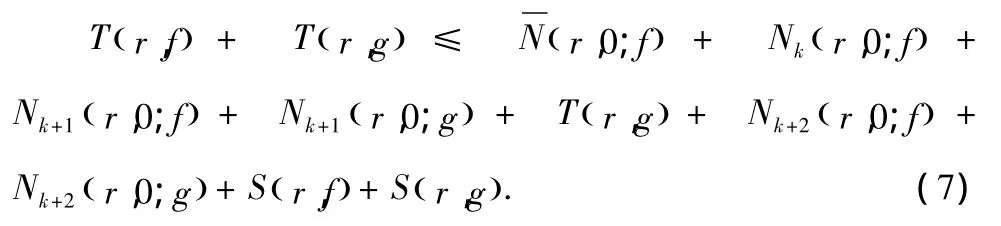
由(7)式有

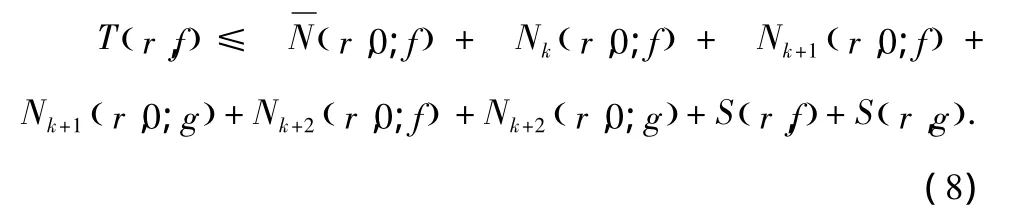
不妨设，存在一个具有无限测试的集合使得T(r，g)≤T(r，f)当 r∈I.因此

当 r∈ I及0 ＜ ε ＜ Δ1-5，于是{Δ1-5- ε}T(r，f)≤S(r，f)i.e.

Δ1-5≤0，

i.e.

Δ1≤5，

由Δ1＞5，这样就产生了矛盾.

因此H≡0，那么

孙岩国举例，在门诊大厅扫描支付二维码，输入姓名、电话号码和身份证号，选择诊室，页面将迅速弹出挂号成功信息。就诊后，医嘱的化验采血信息及时“导航”，显示相关科室地点及距离。医生开药次日早晨，提醒服药的信息已发送至患者手机，“想忘记吃药都难”。整个过程，省却了排队挂号、交费的烦恼，也不再受找不到诊室而困扰。“最重要的是开通了住院预交金，一日清单、体验登记和报告书等移动支付项目，医保的二次结算也可顺利实现。”

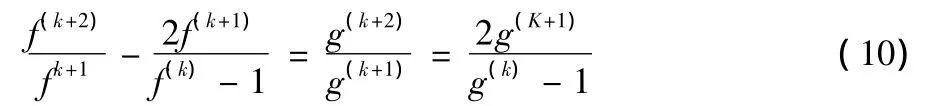
解上述微分方程得到

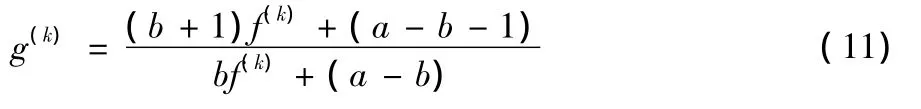
这里a(≠0)，b为两个常数.

接下来分三种情形讨论.

情形1:b≠0，-1.若a-b-1≠0，由(11)有

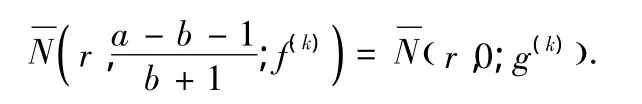
再根据引理2.1有

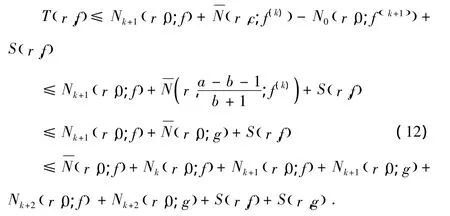
这样由(1)，我们得到Tr，()f≤Sr，()f，r∈I，矛盾.

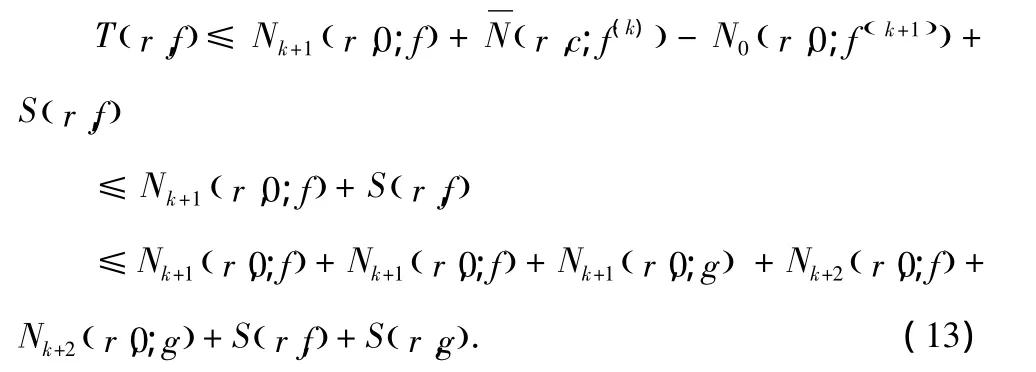
那么由(1)式得到 T(r，f)≤ S(r，f)，r∈ I，矛盾.

若a+1≠0，那么a+1为f(k)的一例外值.类似于情形1可得到矛盾.

若 a+1=0，那么 f(k)g(k)≡1.

情形3:b=0:由(11)式得到g(k)=(f(k)+a-1)/a.

若a-1=0，那么f(k)≡g(k).解此方程，有

f=g+p(z).

这里 p(z)为多项式.由上式有 T(r，f)=T(r，g)+S(r，f).

若 P(z)≠0，由引理 2.2，得到

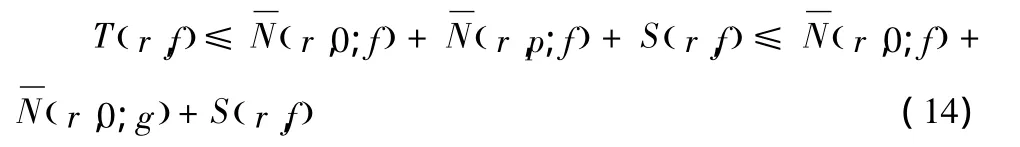
因此，可以得到

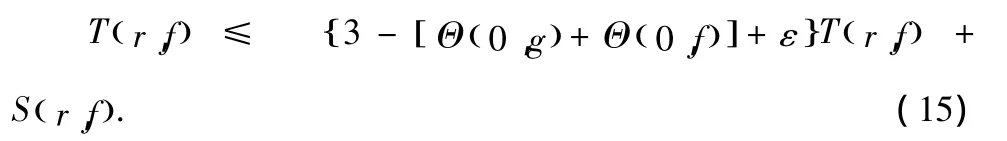
其中0＜ ε ＜1-δk+1(0，f)+1-δk+2(0，f)+1-δk+2(0，g).

于是有 {Δ1-5}T(r，f)≤ S(r，f).

因此由(1)，可得到 T(r，f)≤ S(r，f)，r∈ I，又一矛盾.

那么可知p(z)≡0，于是f≡g.

引理 2.10［2］:若 f1(z)，f2(z)，…，fn(z)为不同亚纯函数以及g1(z)，g2(z)，…，gn(z)为整函数，满足

(ii)当时，为非常数，

那么 fj(z)≡0(j=1，2，…，n).

3 定理的证明

定理 1.1 的证明:令 F=fn，G=gn.这样就有

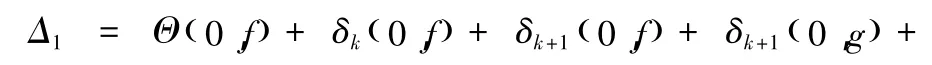
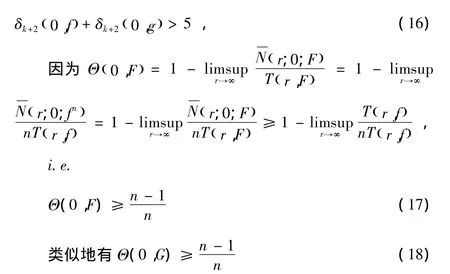
由Nk(r，a;f)的定义知

由(16)－(23)可以得到

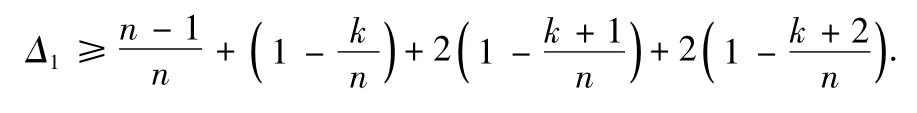
由于n＞5k+7可得Δ1＞5.

由于F(k)=(fn)(k)及G(k)=(gn)(k)，再根据定理1.1的条件知，F(k)，G(k)分担(1，0)以及F，G满足引理2.9的条件.

下面分两种情形讨论.

情形1:F(k)G(k)≡1;

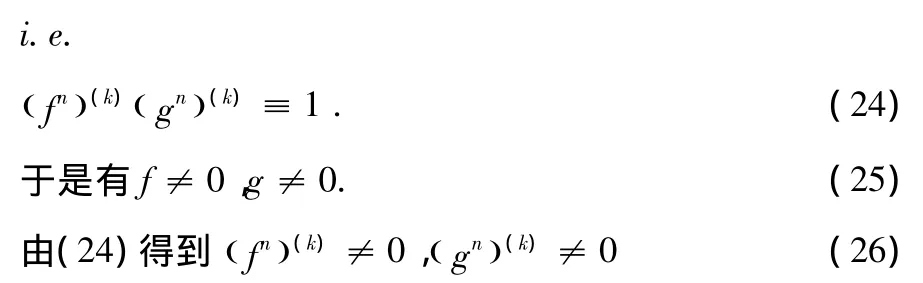
再根据(24)，(25)，(26)及引理2.4，当 k≥2 时，我们有，这 里 C1，C2，C3为 常 数 且 满 足

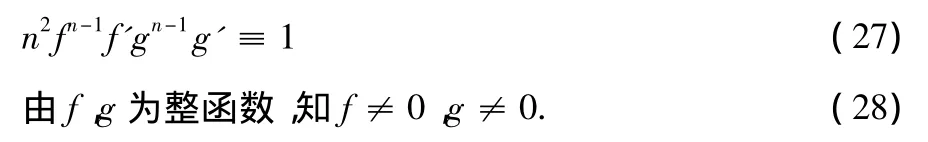
i.e.，n(eμ+eν)+ μ′+ ν′≡ 0.那么由(31)可得到

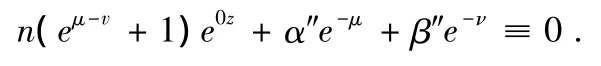
再根据引理 2.10，可得 eμ-ν+1=0，i.e.，eμ-ν=-1.于是

μ-ν=(2m+1)πi，对某个整数m，

i.e.，

μ =v+(2m+1)πi，对某个整数m.

将上式代入(32)得到μ′=ν′≡0，于是μ=ν为常数i.e.α′，β′也是常数.

这样由(26)－(31)，得到 f=c1ecz，g=c2e-cz，这里c1，c2.c为常数，满足(-1)k(c1c2)n(nc)2k=1.

综合以上过程知:若 F(k)G(k)=1，k≥1，有f=c1ecz，g=c2e-cz，这里 c1，c2，c为三常数，满足(-1)k(c1c2)n(nc)2k=1.

情形 2:F≡G，i.e.fn≡gn.这时可得 f=tg，其中 tn=1.

综合情形1与2，就可得到定理1.1.

［1］Hayman W K.Meromorphic Functions［M］.Oxford:The Clarendon Press，1964.

［2］Yang C，Yi H.Uniqueness theory of meromorphic functions［M］.Beijing:Science Press，1995.

［3］Frank G.Eine Vermutung von Hayman uber nullstellen meromorphic function［J］.Math Z，1976，149:29－36.

［4］Banerjee A.Meromorphic functions sharing one value［J］.Int J Math Sci，2005，(22):3587－3598.

［5］Lahiri I.Weighted value sharing and uniqueness of meromorphic functions［J］.Complex Variables Theory Appl，2001，(3):241－253.

［6］Lahiri I.Value distribution of certain differential polynomials［J］.Int J Math Sci，2001，28:91－93.

［7］Lahiri I.Weighted sharing and uniqueness of meromorphic functions［J］.Nagoya Math J，2001，161:193－206.

［8］Lahiri I，Sarker A.Uniqueness of a meromorphic functionand its derivative［J］.J Inequal Pure Appl Math，2004，(1):Article 20.