储粮熏蒸过程中磷化氢浓度的分布模型及验证研究

王远成 Graham R Thorpe 赵会义 曹 阳 魏 雷

（山东建筑大学热能工程学院1，济南 250101）

（教育部可再生能源建筑利用技术实验室2，济南 250101）

（澳大利亚维多利亚大学工程与科学学院3，墨尔本 8001）

（国家粮食局科学研究院4，北京100037）

储粮熏蒸过程中磷化氢浓度的分布模型及验证研究

王远成1，2Graham R Thorpe3赵会义4曹 阳4魏 雷4

（山东建筑大学热能工程学院1，济南 250101）

（教育部可再生能源建筑利用技术实验室2，济南 250101）

（澳大利亚维多利亚大学工程与科学学院3，墨尔本 8001）

（国家粮食局科学研究院4，北京100037）

谷物在长期储存过程中会受到害虫的侵扰，通常需要使用诸如磷化氢等适量的熏蒸剂对仓储粮食进行熏蒸，从而杀死害虫，同时又要避免害虫产生耐药性和熏蒸剂的残留。本研究首先建立和验证了熏蒸剂（磷化氢）的对流扩散和吸附模型，并采用计算流体动力学方法对圆筒仓内谷物熏蒸过程中磷化氢质量浓度进行了数值预测，分析了熏蒸过程中磷化氢的质量浓度分布规律，得出熏蒸过程中磷化氢质量浓度分布是不均匀的，并且受到谷物吸附和不可逆化学反应的双重影响。

谷物存储 熏蒸剂 对流扩散 数值模拟 圆筒仓

谷物在长期储存过程中会受到害虫的侵扰，通常需要使用诸如磷化氢等熏蒸剂对储粮进行适度熏蒸，从而杀死害虫，因此熏蒸被广泛地用于储粮系统的害虫防治。尽管高效低廉的磷化氢等熏蒸剂的使用可以有效杀死粮仓内的害虫，但是过量长期使用熏蒸剂，一方面会使得害虫产生耐药性，另一方面可能导致熏蒸剂在粮食中的残留。由于绝大多数谷物被加工成食品，谷物在熏蒸后的残留受到严格限制。如何制定熏蒸剂的剂量，使得既能杀死害虫又能保证合乎标准的残留量是粮食仓储企业面临的一个关键问题。因此，科学设计熏蒸工艺，了解谷物熏蒸过程中熏蒸剂的扩散以及谷物对熏蒸机的吸附，掌握熏蒸过程中熏蒸剂的浓度演化规律，对于科学储粮具有重要的现实意义。

以往对谷物熏蒸过程的研究大多采用实验室研究和现场测定的方法。Darby［1］根据试验研究提出了谷物吸附熏蒸剂的数学模型。但是由于其试验是在烧瓶内完成的，烧瓶的尺度远远小于实际粮仓的尺度，因此，熏蒸剂的很快扩散到整个烧瓶的谷物中，而且各处的熏蒸剂浓度基本相同，显然这与实际情况是有出入的。现场观测的方法是国内使用较多的方法，但这种方法需要大量人力物力的消耗，而且很难准确地控制测量精度。实际上谷物在熏蒸过程中，熏蒸剂在谷粒间的对流扩散过程是一个非常复杂的过程，一方面由于强制对流或自然浮生对流作用，熏蒸剂在谷物颗粒之间进行对流扩散，同时，谷物颗粒对熏蒸剂吸附以及二者之间的不可逆反应，导致粮堆中熏蒸剂的浓度在空间和时间上是连续变化的。

基于质量守恒和动量守恒的计算流体动力学方法可以有效地描述谷物熏蒸过程中熏蒸剂的运动和浓度分布规律，也是近年来国际上流行的研究流动和传热传质问题的新方法。计算流体动力学（Computational Fluid Dynamics-CFD）的基本思想可以归结为：把原来在时间域及空间域上连续分布的物理量的场，如速度场、温度场和浓度场等用一系列有限个离散点上的变量值的集合来代替，通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组，然后求解代数方程组获得场变量的近似值。因此，CFD可以看作是在流动基本方程（质量守恒方程、动量守恒方程、能量守恒方程）控制下对流动及传热传质过程的数值仿真。通过这种数值模拟，可以得到极其复杂问题的流场内各个位置上的基本物理量（如速度、压力、温度、浓度等）的分布，以及这些物理量随时间的变化情况［2］。

本研究的目的是要建立熏蒸剂在谷物颗粒之间对流扩散的数学模型，模型同时考虑谷物对熏蒸剂的吸附和不可逆化学反应。依据所建立的数学模型，采用数值模拟的方法模拟熏蒸过程中圆筒仓内部谷堆内部熏蒸剂（磷化氢）的质量浓度分布及其演化规律。

1 数学模型

1.1 谷物颗粒床中熏蒸剂对流扩散方程

考虑熏蒸剂气化后为磷化氢气体，因此，根据多孔介质中气体流动和组分输运方程可以得到［3］：

式中：u为空气的表观速度或达西速度；P为压力；t为时间；Δ为微分算子；μ为空气的动力黏度；Si为动量方程的源项，即粮堆中空气流动的阻力［4］为谷粒床的空隙率；ρa为颗粒间空气的密度；φ为谷物颗粒床中熏蒸剂（磷化氢）的质量浓度；Deff为熏蒸剂通过颗粒床的有效扩散系数；Sφ为谷物对熏蒸剂吸附或解吸附速率

1.2 粮粒对磷化氢吸附和反应动力学模型

Darby［1］已提出考虑谷物颗粒对磷化氢吸附及不可逆反应的时间变化率模型。

式中：c为磷化氢质量浓度／mg／L；ssorp为比表面积／m2／m3；kf为谷粒外表面的传质阻力／m／s；C为被颗粒吸附的熏蒸剂的质量浓度／mg PH3／L。

式中：F为分配系数／m3／m3；cs为吸附达到热力学平衡时气体磷化氢的质量浓度／mg／L。

由 Darby［1］报告可知：

式中：n为指数；kbind为不可逆化学反应系数／s-1（mg／L）（1-n）。

1.3 物性参数

磷化氢的扩散系数可以用Chen等［5］公式描述，即二元气体双扩散的计算方程为：

式中：A和B为2种不同气体，A为磷化氢气体；B为空气；θ表示绝对温度；M为分子质量；θC和VC分别为临界温度和体积／m3／kmol。根据 Air Liquide［6］，磷化氢的 θC为324.75K，其临界体积 VC根据Chen等［5］的研究，有：

式中：σ为磷化氢分子的Leonard-Jones碰撞直径，根据Kee等［7］研究结果，σ为3.981Å。Wark等［8］研究表明磷化氢的分子质量为33.997，临界体积为0.117 196 m3／kmol。空气的临界温度和压力分别为132.5K和0.088 3 m3／kmol，并且其分子质量为28.97。当空气温度为25℃，空气密度为1.184 1 kg／m3时，由式（6）计算得到磷化氢的扩散系数为 1.57×10-5m2／s。

2 模型验证

为了验证本研究建立的数学模型，根据Darby［1］的熏蒸试验条件，分别对4种不同的磷化氢初始质量浓度下小麦的熏蒸试验系统中磷化氢扩散的质量浓度分布进行数值模拟预测，通过比较数值模拟结果和直接求解Darby［1］方程得到的磷化氢质量浓度来验证模型的合理性。4种情况涉及到小麦储藏系统中同时存在磷化氢的吸附和不可逆化学反应过程。试验系统由小麦和空气组成，其中小麦占整个空间的95%，磷化氢的初始质量浓度分别为3.0、1.0、0.3和0.1 mg／L。图1是采用本研究建立的数学模型的数值模拟计算和直接求解Darby［1］方程得到的磷化氢质量浓度，从图1可以看出，二者之间完全相符，也说明此数学模型是合理的。

需要说明的是图1给出的利用建立的数学模型进行数值模拟计算和直接求解Darby［1］模型的使用条件略有不同，Darby［1］在测定前摇动烧瓶一定时间后才进行测定的结果，而在数值模拟计算时考虑谷堆内部和谷堆上部空气中的磷化氢扩散，然而，数量级分析发现，磷化氢在谷堆内扩散进行的时间约为1 000 s，它是实验室试验时间的10%，这也说明摇动烧瓶并不能提高磷化氢的扩散。

图1 Darby［1］模型计算结果与本模型的模拟计算结果比较

3 数值模拟结果和分析

基于已经验证的数学模型，采用CFD的方法对部分填充谷物的圆筒仓进行磷化氢熏蒸过程中磷化氢质量浓度进行了数值模拟计算。选取试验仓为一小型的圆筒仓，直径为6 m，圆柱段高度为6 m，体积为182 m3，仓内小麦的体积为154 m3，如图2所示。熏蒸剂通过位于筒仓圆柱段底端以上0.1 m处的直径为0.05 m的进口以1.0 L／s的空气流量、35 mg磷化氢／L空气被送入圆筒仓，然后通过圆筒仓上部的出口流出。数值模拟中圆筒仓的网格为四边形网格，网格数为50 289。

图2 圆筒壁设有直径0.05 m熏蒸剂入口的圆筒仓示意图

数值模拟分为2种情况：一是圆筒仓内存储棉籽；二是圆筒仓内存储小麦。图3显示的是熏蒸通风100 h圆筒仓内棉籽中的磷化氢质量浓度分布。从图3可以看出，熏蒸剂在仓内分布并不均匀，在熏蒸入口处磷化氢的质量浓度最高。由于扩散和吸附的作用，圆筒仓左上部磷化氢质量浓度较低，而棉籽上部的空气区右半部分的磷化氢质量浓度较高，说明部分未被吸附的磷化氢气体从圆筒仓粮堆的右上部通过出口排除，造成熏蒸剂的损失，同时可能在圆筒仓的谷堆左上部还未达到害虫致死剂量，这也说明了该熏蒸系统的设计存在一定的缺陷而需要改进。

图4显示的是不同熏蒸通风时间后圆筒仓内小麦中的磷化氢质量浓度分布。可以看出，在1～10 h熏蒸通风时间内，在熏蒸入口处磷化氢的质量浓度最高，但熏蒸剂并未扩散到整个仓内。20～40 h熏蒸通风时间内，熏蒸剂已经扩散到整个仓内，但是由于吸附作用，仓左上部磷化氢质量浓度仍然较低，20 h为2 mg／L，40 h为 17 mg／L。随着熏蒸时间的增加，仓左上部磷化氢质量浓度逐渐升高，达到80 h后，入口处磷化氢的质量浓度最高为35 mg／L，仓左上部粮堆内磷化氢质量浓度达到27 mg／L，约为进口处的80%，但仓内的磷化氢质量浓度仍然没有达到均匀状态。当熏蒸通风时间达到1周（160 h）后，仓内磷化氢最低质量浓度为32 mg／L，接近入口的质量浓度。而且在80 h后关闭吸附项进一步模拟，即数值模拟中不再考虑粮粒对磷化氢的吸附时，发现此时仓内磷化氢最低质量浓度约为34 mg／L，这表明谷粒不再吸附磷化氢。

比较图3和图4可以发现，在相同时间内棉籽和小麦内磷化氢的质量浓度是不同的，其原因主要在于棉籽堆和小麦堆的孔隙率不同，而且棉籽对磷化氢的吸附能力高于小麦。

图3 熏蒸通风100 h后圆筒仓内棉籽磷化氢质量浓度（mg／L）分布

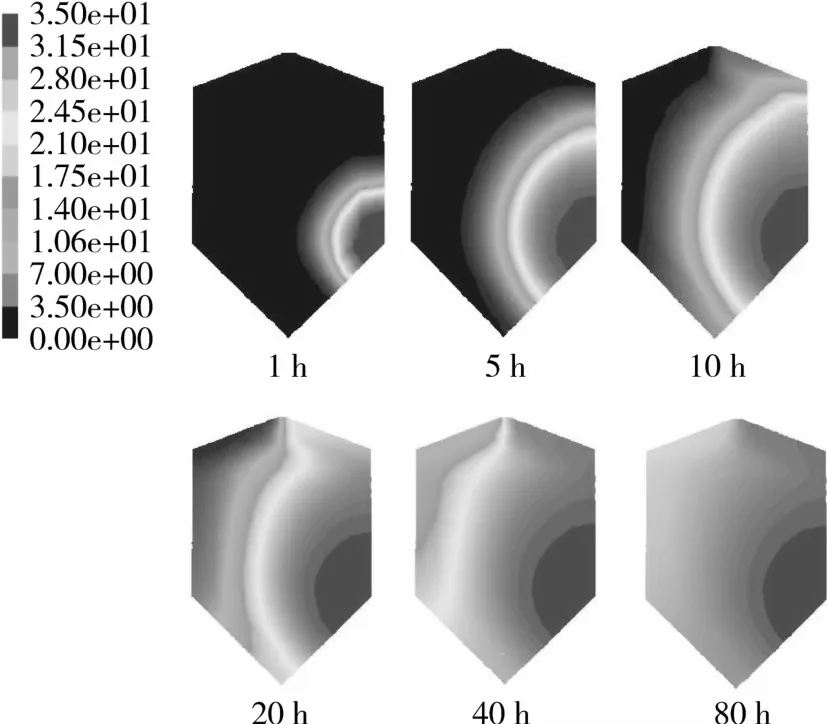
图4 熏蒸通风不同时间后仓内磷化氢质量浓度（mg／L）的演化规律

4 结论

首先依据Darby［1］吸附动力学模型，建立了多孔介质内部熏蒸剂的对流扩散模型，模型考虑了谷物对磷化氢吸附和化学反应作用的影响，通过与Darby［1］的经验方程计算结果进行比较后，验证了本研究建立的数学模型的合理性。

采用CFD方法对试验圆筒仓内谷物的熏蒸过程进行了数值预测，CFD计算结果表明熏蒸通风初期（1～10 h）磷化氢的分布是不均匀的，它不仅受到磷化氢对流扩散速度的影响，而且还受到谷物吸附和不可逆化学反应的双重影响。40 h后，熏蒸剂已经扩散到整个仓内，但是由于吸附作用，仓左上部磷化氢质量浓度仍然较低，约为17 mg／L。达到80 h后，仓左上部粮堆内磷化氢质量浓度达到27 mg／L，约为进口处的80%，当熏蒸通风时间达到1周（160 h）后，仓内磷化氢最低质量浓度为32 mg／L，接近入口的浓度。对于小麦来说，在该熏蒸工艺条件下，大约需要通风1周时间，而棉籽则需要更长的时间才能达到较好的熏蒸效果。

［1］Darby J A.A kinetic model of fumigant sorption by grain using batch experimental data［J］.Pesticide Management Science，2008，64：519-526

［2］王远成，张忠杰，吴子丹，等.计算流体力学技术在粮食储藏中的应用［J］.中国粮油学报，2012，27（5）：86-91

［3］Thorpe G R，Ochoa-Tapia JA and Whitaker S.The diffusion ofmoisture in food grains.II：Estimation of the effective diffusivity［J］.Journal of Stored Products Research，1991，27：11-30

［4］Wang Yuancheng，Duan Haifeng，Zhang Hao，et al.Modeling on Heat and Mass Transfer in Stored Wheat during Forced Cooling Ventilation［J］.Journal of Thermal Science，2010，19（2）：167-172

［5］Chen N H and Othmer D F.New generalized equation for gas diffusion coefficient［J］.Journal of Chemical and Engineering Data，1962，7：37-41

［6］http：／／encyclopedia.airliquide.com／Encyclopedia.asp？GasID＝51［EB／OL］，2012

［7］Kee R J，Dixon-Lewis G，Warnatz J，et al.A FORTRAN computer code for the evaluation of gas-phase，multicomponent transport properties［G］.Sandia National Laboratories Report，Version superceding SAND86-8246B，1998

［8］Wark K and Richards D E.Thermodynamics，6thEdition［M］.WCB／McGraw-Hill，1999：1029-1050.

The Model and Validation of Phosphine Fumigation in Stored Grains in Silos

Wang Yuancheng1，2Graham R Thorpe3Zhao Huiyi4Cao Yang4Wei Lei4

（College of Thermal Energy Engineering，Shandong Jianzhu University1，Ji′nan 250101）
（Key Laboratory of Renewable Energy Utilization Technologies in Buildings of the National Education Ministry2，Ji′nan 250101）
（College of Engineering and Science，Victoria University3，Melbourne，Australia 8001）
（Academy of State Administration of Grains4，Beijing 100037）

Grains should be stored free from insect pests.Insects that infest stored grains in all life stagesmay be killed by being fumigated with poisonous gases as phosphine.In the paper，amathematicalmodel for convective diffusion and sorption of fumigants to be used in stored grains has been developed to be implemented by Computational Fuid Dynamics（CFD）.Themodel has been compared with published results and found to have excellent result.It is shown that the fumigation is non-uniform and the spatial distribution of fumigant can be affected by grain kernels＇adsorption aswell as the non-reversible chemical reaction.

stored grains，fumigation，convection and diffusion，numerical simulation，silos

S379.5；TK124

A

1003-0174（2015）07-0081-04

国家自然科学基金（51276102），山东省自然科学基金（ZR 2011EEM011）

2014-03-04

王远成，男，1963年出生，教授，生物性多孔介质传热传质