基于季节调整的核心通货膨胀度量

■ 赵鹏飞 袁 霓 副教授（中国青年政治学院经济管理学院北京 100089）

学者们对核心通货膨胀的定义虽有不同，但都认为核心通货膨胀反映了价格变动的长期稳定的趋势。中国人民银行在季度报告中给核心通货膨胀进行了界定，将其表述为“从总通货膨胀中剔除暂时性因素影响的潜在通货膨胀，用来反映价格变动的长期趋势”。本文采用中国人民银行给出的界定，对核心通货膨胀进行度量。

核心通货膨胀的度量方法

本文在CPI的基础上，对核心通货膨胀度量。文中标题通货膨胀指统计局公布的CPI，核心通货膨胀指核心CPI。

核心通货膨胀的度量一般有统计途径和建模途径两大类方法。在统计途径方面，基于消费者物价指数的构成情况，可以运用不同方法进行核心通货膨胀的度量。其中，剔除法因计算原理简单，便于理解，被世界各国或地区中央银行普遍采用。在计算核心通货膨胀时，各国所剔除的成分却不尽相同。表1列出了主要经济体计算核心通货膨胀时剔除的成分。此外，剔除法存在着一定的不足。汤丹（2013）认为，各类商品价格指数的波动并不是一成不变的，某些可能随着时间的推移变得相对平稳，而有些可能随着时间的推移波动性变大。固定剔除某些项目，度量出的核心通货膨胀可能存在较大的偏差。

在建模途径方面，从时间序列视角，处理方法为基于序列自身特点，通过平滑或过滤剔除CPI序列的短期“噪音”成分，从而将剩下的长期趋势作为对核心通货膨胀的测度。这种方法更加接近通货膨胀的长期稳定趋势。

Cogley（2002）提出指数平滑法用以描述通货膨胀的长期趋势，该方法采用递减的权重对当前和过去的通货膨胀率进行加权平均，表示为

指数平滑法的关键在于外生变量m的选取。汤丹（2013）运用Cogley的指数平滑法，设定参数m为0.125，选取2001年1月至2011年4月间的月度同比CPI数据，估计中国核心CPI。但是实证表明，中国核心CPI的均值为102.02，标准差为1.638，核心CPI相对CPI具有明显的滞后性。

本文在前人研究的基础上，发现鲜有学者应用季节调整的方法对核心CPI进行度量，更多地是采用季节调整的方法进行CPI的拟合与预测。

张鸣芳等（2004）对上海月度CPI进行实证研究，通过X-12-ARIMA进行季节调整，并考虑春节因素的影响，进一步运用TRAMO/SEATS进行调整。不足的是，缺少对实证结果的具体分析，只给出了未来24个月上海CPI变动情况。

栾惠德（2007）采用PBC版时间序列X-12-ARIMA对中国月度CPI进行季节调整，得到环比CPI和同比CPI，发现环比CPI走势领先于同比CPI，在对经济转折点的判断上比同比CPI领先2到6个月，并对CPI进行了短期预测。

贺凤羊（2011）基于X-12-ARIMA程序中缺少对中国春节等移动假日的调整，提出了改进的X-12-ARIMA-BHG和X-12-ARIMA-LZ的方法，对1997年1月至2010年11月的CPI进行季节调整，反映CPI的发展趋势，同时对2010年12月至2011年6月的同比CPI进行预测。

本文借鉴季节调整的方法，对核心CPI进行拟合和预测，采用X-12-ARIMA模型对定基比CPI进行季节调整，同时考虑到春节因素的影响，构造虚拟变量，运用 TRAMO/SEATS程序对春节效应进行调整，得到最终的长期趋势，即核心CPI。

实证分析

（一）数据的选取与处理

在度量核心通货膨胀时，学者们大多使用同比消费者物价指数进行处理。但是，同比物价指数具有“基数效应”，不能反映当期物价指数真实波动状况。环比指标虽然可以反映当期通货膨胀的真实变动，但环比指标具有季节效应，而且波动剧烈。

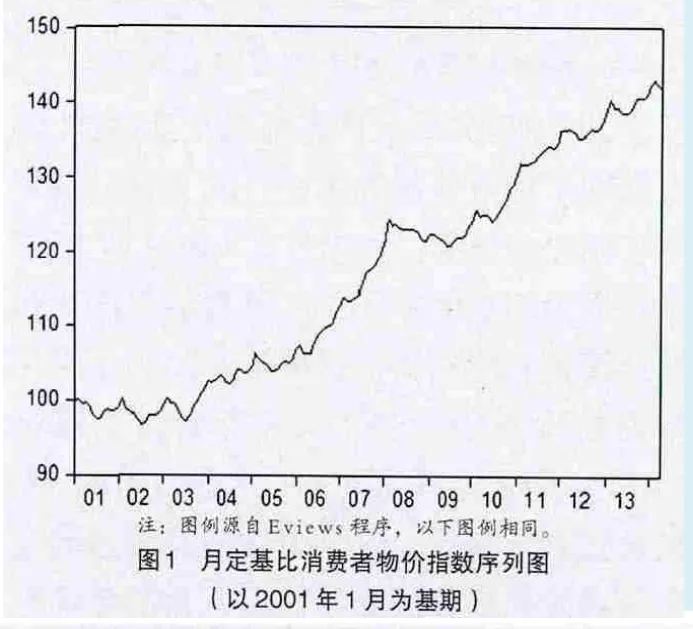
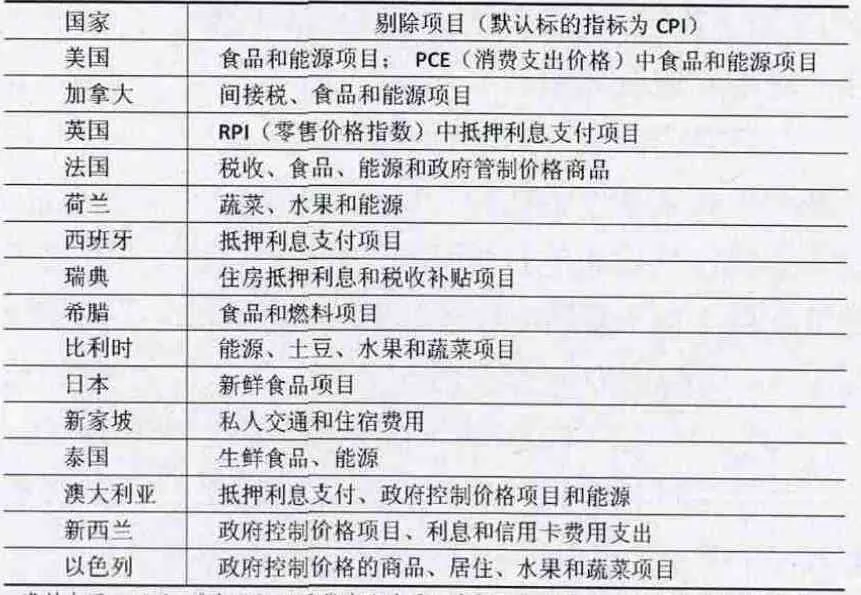
表1 各国度量核心通货膨胀率所剔除的成分

表2 自动探测外部影响表

表3 回归因子组合的卡方检验表

图2 月定基比CPI（DCPI_2001）与季节调整后序列（DCPI_2001_SA）比较图

图3 月定基比CPI序列（DCPI_2001）与核心CPI序列（CoreCPI）比较图

贺凤羊和刘建平（2011）认为一般情况下，时间序列季节调整都是在定基比（固定基期）指数的基础上进行的，这样调整才有明显的效果。张鸣芳（2004）以1993年各月为初始值（100），然后通过同比指标计算定基比指标；贺凤羊（2011）采用相同处理方法，以1996年各月为基期（100）。但是这样得到的“定基比指标”不是真正的定基比，这种方法没有考虑到定基各月间的指标的变动情况。为避免指标的不准确，本文采用环比指标计算定基比CPI（以下简称DCPI），然后在DCPI的基础上对核心进行度量。

自2001年起，中国开始与国际接轨，计算和公布定基价格指数。因此，本文选取国家统计局公布的月度环比全国消费者物价指数（以下简称HCPI），数据范围为2001年1月至2014年4月。

（二）X-12-ARIMA季节调整

为了估计核心通货膨胀，需要剔除季节效应。使用X-12-ARIMA方法进行季节调整，以分离出通货膨胀的长期趋势，即核心通货膨胀。

首先对HCPI进行处理，调整为月定基比消费者物价指数（即DCPI_2001）。DCPI_2001以2001年1月为基期，指数为100（见图1）。

从图1可以看出，每年年初指数居高，然后呈下降趋势，到每年的7～9月开始回升直至年末，这可能受我国春节的影响，每年的年初和年末价格指数高企。同时，可以发现2008年出现了一次转折。2008年美国“次贷危机”的发生对中国经济产生了一定的影响，表现在CPI上，指数呈下降趋势。由于4万亿投资的推出，经过2008年和2009年的调整，经济开始升温，CPI呈上升趋势。整个序列反映了经济的发展状况，存在一个每年基本相同的周期性趋势，表明该序列存在年内的季节性变化。

采用X-12-ARIMA对DCPI_2001进行季节调整。自动诊断发现存在AO2008.Feb，且显著（见表2）。需要注意的是regARIMA程序可以由用户自己指定拟剔除的异常值，也可由程序自动剔除。本文采用自动剔除异常值的功能。

另外，在regARIMA过程中，回归方程中加入了交易日和闰年回归元，样本容量为160，回归方程如下：

该方程的回归因子由交易日、闰年和一个异常值组成，括号中对应各个参数的t值。交易日联合显著性检验发现交易日影响不显著，但是交易日和闰年的联合检验显著，说明闰年对CPI的变动影响较大（见表3）。

在进行季节调整前，先对季节效应进行F检验，发现参数和非参数季节效应显著。同时，移动季节效应在5%水平下显著，结果表明DCPI_2001序列适合进行季节调整。

在ARIMA模型的选取上，采用样本外预测残差平方和最小的标准，程序选取（0，1，1）（0，1，1）模型进行预调整。

程序输出报告给出了11个用于质量监控的M统计量，每个统计量的取值范围都在0～3之间。如果M统计量的数值小于1，则表明季节调整效果良好；否则表示调整的效果欠佳。本文所得到的调整结果，发现11个M统计量的数值均小于1，表明季节调整效果良好（见表4）。

为了直观地体现季节调整的效果，将原序列和调整后序列进行比较（见图2）。

经过季节调整之后，对残差序列进行季节效应检验，发现在整个序列水平以及最后三年的检验均在1%的水平拒绝残差序列存在季节效应，表明季节调整效果显著。

（三）春节效应的调整

春节是中国重要的传统节日。春节期间物价明显要出现上涨，因此对春节效应的调整是不可忽视的。

值得注意的是，在X-12-ARIMA程序中，假期效应的调整针对美国的传统节日设定，并不适用于中国的春节，需要采用其它方法对春节效应进行调整。本文借鉴张鸣芳等（2004）使用TRAMO/SEATS程序，引入一个关于春节的虚拟变量，进一步对物价指数进行调整。

中国春节在每年中的日期具有不确定性，属于移动假日，主要出现在1月份和2月份。参照X-12-ARIMA对复活节的调整方法，建立如下春节模型。假定从春节之前的第n天开始，经济活动的价格水平发生变动并保持在这一新水平上直至节日的前一天。

构造辅助变量Wi(n,t)，表示第i年春节前n天中落入t月份的天数，则构造的春节虚拟变量Pi(n,t)=Wi(n,t)/n，即对于给定的某个月份t，落在t 月份的受到节日影响的时段占整个受影响时段n 的比例。同时借鉴贺凤羊（2011）和栾慧德（2007）的方法，为保证在消除估计的假日影响之后，所得到的序列的年度总和等于原序列的年度总和，对Pi(n,t)进行中心化处理，使调整后的序列是原序列的无偏估计。具体调整如下：

设Pi(n,t)在整个样本区间内的均值为，则中心化后的解释变量

表4 监测及质量评估统计量表

表6 月定基比CPI与核心CPI统计检验一览表

表7 相关CPI的预测值表

另外，参考张鸣芳（2004）的实证分析，设定n=20，得到Pi(n,t)以及中心化处理后Pi*(n,t)的取值情况，见表5。

将中心化处理后的春节变量导入至TRAMO/SEATS程序中，经过调整得到最终的核心CPI序列，并将月定基比CPI序列与核心CPI序列（即CoreCPI）进行对比，见图3。

（四）统计检验

为了验证该方法对中国核心CPI度量的有效性，本文借鉴汤丹（2013）对核心CPI度量方法统计检验，采用波动性检验、平稳性检验、协整检验以及Granger因果关系检验对样本期内（2001年1月至2014年4月）月定基比CPI序列以及核心CPI序列进行分析。

波动性检验，核心CPI是对月定基比CPI长期、稳定趋势的反映，合理的核心CPI的波动要小于月定基比CPI的波动情况。由于序列波动性与标准差有关，因此本文采用标准差作为指标进行检验。经计算发现，月定基比CPI标准差大于核心CPI的标准差（见表6），说明核心CPI通过了波动性检验。

对月定基比CPI序列进行平稳性检验发现，在原序列水平上不平稳，进行一阶差分后，单位根检验显著，序列平稳，说明月定基比CPI序列为一阶单整即I（1），再对核心CPI序列进行检验发现，核心CPI序列同样为I（1）（具体数据见表6）。平稳性检验，是为了保证核心CPI序列与月定基比CPI序列为同阶单整，二者只有保证同阶，对核心CPI的度量才有意义。

由于月定基比CPI序列与核心CPI序列均为I（1），可以进行协整检验。本文采用误差修正模型检验二者间的协整关系，回归方程如下：

回归方程中CPI指月定基比CPI，CoreCPI表示核心CPI。回归发现，α的估计值为负且在1%的水平上显著（具体值见表6），表明月定基比CPI与核心CPI之间存在长期稳定关系，当月定基比CPI偏离核心CPI时，协整关系起到引力线作用，使偏离状态恢复到均衡稳定。

进一步地对二者进行Granger因果关系检验。采用滞后一阶方法，发现月定基比CPI不是核心CPI的格兰杰原因，核心CPI是月定基比CPI的格兰杰原因（具体数据见表6）。

经过一系列的统计检验，表明该方法度量的核心CPI对月定基比CPI的长期、稳定的趋势实现了较好的反映，核心CPI不仅与月定基比CPI具有协整关系，同时月定基比CPI是由核心CPI Granger引起的。可以用核心CPI对月定基比CPI的长期趋势做出较好的预测。

结论

从图3可以看出，核心CPI序列较好地对月定基比CPI序列实现了平滑地拟合，修匀了异常值和过滤了较大的波动，不仅反映了月定基比CPI的长期稳定的走势，也从一定程度上反映了中国在2001-2014年间经济的发展趋势。中国经济因受1997年金融危机的影响，长期处于紧缩状态。虽然采取相应的宏观政策，但经济发展平稳，表现为2001-2003年间核心CPI处于水平态势；直至2004年中国经济开始扩张，2004-2007年间核心CPI处于不断上涨的趋势；2008年的美国“次贷危机”又一次使中国的经济受到了影响，经济增长出现回落，核心CPI虽略有下滑，但长期内保持增长的态势，期间推出的四万亿经济刺激方案出现了成效，2009年末经济开始企稳回升，核心CPI 呈现出上升发展趋势。

由于同比CPI更多地为人们熟知，本文在进行预测时，将得到的定基比核心CPI转换为同比核心CPI，即是，将各期定基比核心CPI与前一年同一时期的定基比核心CPI相比，得出预测期内的同比核心CPI（见表7）。从预测出的趋势来看，2014年5月至2014年9月中国核心通货膨胀（见表7中的第3列）略有下降趋势；从2014年10月至2015年4月有明显的上涨趋势，在1%左右。整体上是呈先下降后上升的平稳态势。实证表明，经季节调整后的核心CPI可以用来对经济的走势进行分析和预测，避免原序列水平不能反映经济长期趋势的不足。

1.伯南克.通货膨胀目标制—国际经验[M].东北财经出版社，2013

2.汤丹.中国核心通货膨胀度量研究[M].社会科学文献出版社，2013

3.张鸣芳，项燕霞，齐东军.居民消费价格指数季节调整实证研究[J].财经研究，2004（3）

4.栾惠德.居民消费价格指数的实时监测—基于季节调整的方法[J].经济科学，2007（2）

5.贺凤羊，刘建平.如何对中国CPI进行季节调整—基于X-12-ARIMA方法的改进[J].数量经济技术经济研究，2011（5）

6.中国人民银行课题组.通货膨胀测度与货币政策[J].经济学动态，2011（6）

7.周小川.《分析物价趋势的指标选择》[J].统计与精算，2013（4）