钢筋高强混凝土偏压中长柱承载力研究

杨荣华，焦俊婷

(厦门理工学院土木工程与建筑学院，福建厦门 361024)

0 引言

我国大力提倡建设资源节约型、环境友好型社会，随着高强、高性能混凝土应用逐渐推广，加之建筑师强调建筑个性特点，钢筋混凝土结构中长柱在工程中已时有应用，中长柱破坏可能发生材料强度破坏或失稳破坏．国内外现有文献对钢筋混凝土中长柱研究已取得一些研究成果［1－9］．张光玮［1］、张健等［2］分别对重庆大剧院的C40、C60细长柱进行了试验研究和理论分析．刁波等［3］采用段长法对任意截面钢筋混凝土柱的稳定进行了简化计算，理论计算与试验结果吻合较好．魏巍等［4］利用柔度法编制的非线性程序分析了钢筋普通混凝土柱的极限承载力．蒋秀根等［5］利用有限元法分析了普通混凝土长柱的力与挠度全过程加载的曲线关系．薛建阳等［6］对型钢再生混凝土长柱恢复力模型进行了试验研究，基于试验数据给出型钢再生混凝土长柱恢复力的特征参数计算方法．王卫华等［7］用ABAQUS 非线性有限元软件分析了初始偏心距对钢筋混凝土短、中、长柱受压承载力的影响．石立彬［8］研究了钢筋混凝土细长柱受地震作用时受力情况，提出长柱的设计建议．王依群等［9］基于模型柱法提出了钢筋混凝土细长圆形截面柱承载力计算公式．现有文献主要对钢筋普通混凝土中长柱、细长柱承载力进行研究［3－9］，而对钢筋高强混凝土中长柱、细长柱承载力的研究较少［1－2］．鉴于此，深入开展钢筋高强混凝土中长柱、细长柱承载力研究是必要的．

在焦俊婷等［10］建立的梁柱单元模型基础上，对C50、C60、C70、C80钢筋高强混凝土偏压中长柱进行多种工况数值分析，对钢筋高强混凝土偏压中长柱承载力主要影响因素长细比λ(λ=l0/h)、相对偏心距e(e=e0/h，e0为轴压力的初始偏心距)、混凝土强度fc、纵筋配筋率ρ等因素进行分析，并分析了钢筋高强混凝土偏压中长柱承载力的敏感因素，最后拟合出钢筋高强混凝土偏压中长柱极限承载力Nu的计算公式，为实际工程应用提供计算参考．

1 单元模型

1．1 基本假设与材料本构模型

作如下假设:①平截面假设;②忽略截面剪切力对截面变形的影响;③ 钢筋与混凝土之间充分粘结，无相对滑移;④钢筋的应力－应变关系为理想弹塑性(混凝土受压应力－应变关系采用文献［11］中本构模型，忽略混凝土受拉应力);⑤柱截面加载前后始终垂直其轴线．

1．2 单元刚度

依据虚功原理推导考虑材料非线性和几何非线性耦合，建立了梁柱单元模型［10］:

1．3 编程与计算程序的验证

基于梁柱单元模型，用梁柱单元模型矩阵组装结构的整体矩阵，为能够跟踪结构计算的下降段采用弧长增量迭代法求解非线性方程组．用Fortran语言编制了钢筋高强混凝土偏压柱非线性分析程序．用所编制的程序，对文献［12］中试件进行计算，并将计算结果与试验数据进行比较，结果如表1所示，二者吻合较好，表明程序可行．

表1 理论计算与试验数据的比较Tab．1 Comparison of theoretical results and test data

2 偏压中长柱承载力的数值分析

2．1 偏压中长柱破坏与承载力主要影响因素

研究指出钢筋混凝土中长柱承载力比截面承载力复杂，其承载力受构件几何尺寸、支撑约束、刚度、材料等影响，二阶弯矩与初始弯矩叠加共同决定其承载力，既有材料非线性也有几何非线性［1－2，4－5］．如图1所示，柱的破坏形式有材料破坏和失稳破坏．其中，Nu表示偏压柱的受压极限承载力，w1表示柱跨内最大挠度．中长柱由于二阶弯矩的影响，经常发生失稳破坏，柱失稳破坏的承载力低于材料破坏的承载力．

现有试验与理论研究表明，钢筋高强混凝土偏压中长柱承载力的主要影响因素有:长细比λ(l0/h)、相对偏心距e(e0/h)、混凝土强度fc和纵筋配筋率ρ等．

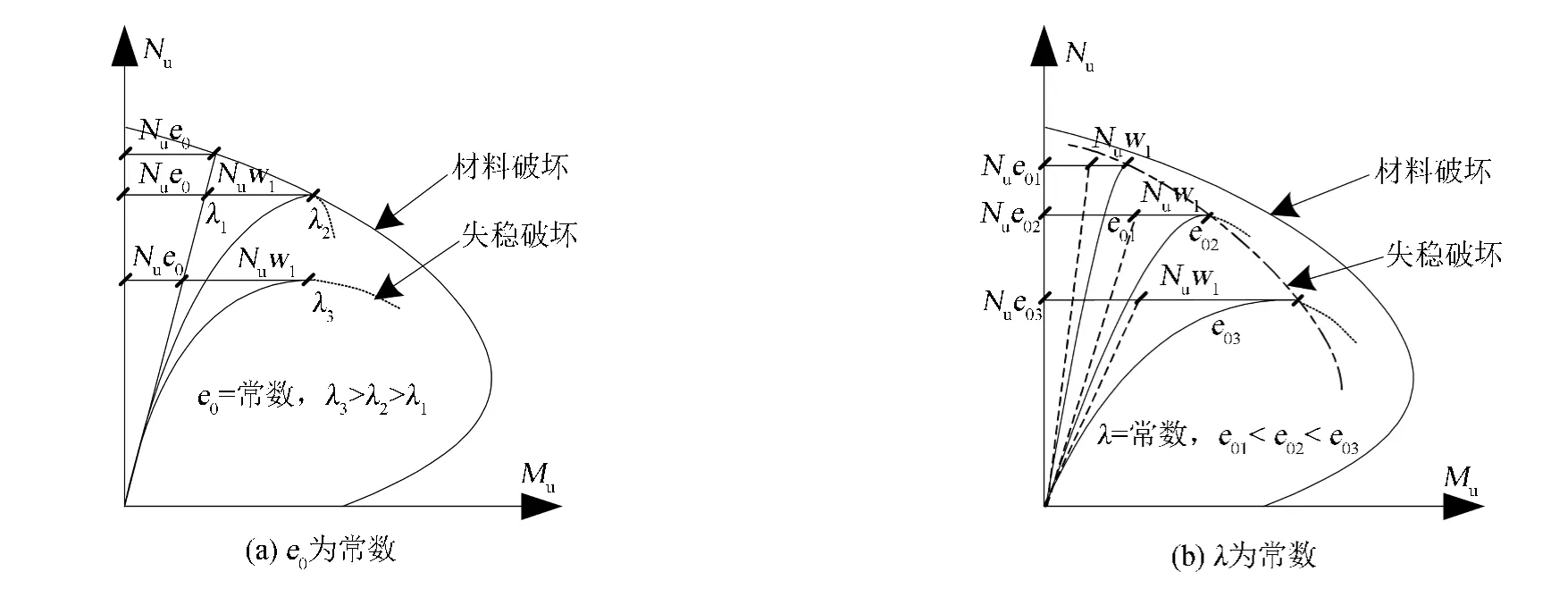
图1 偏压柱的破坏Fig．1 The column failure under eccentric compression

2．2 计算工况

为了较全面了解各影响因素对钢筋高强混凝土偏压中长柱承载力的影响，分别采用不同的λ、e、fc和ρ等多工况，计算铰支等初始偏心距e0的中长柱极限承载力，对比分析各参数对偏压中长柱极限承载力的影响．具体计算工况参数见表2，共5×43=320种不同工况，柱截面配筋如图2所示．

表2 计算工况Tab．2 Calculation conditions

图2 柱截面Fig．2 The column section － cross

2．3 各因素对偏压中长柱极限承载力的影响

为了较好地了解各影响因素对偏压中长柱极限承载力的影响规律，采用增大因子η，即:将其它参数固定，而只改变某一个参数X，该参数取值为X1＜X2＜… ＜Xn，其对应的极限承载力分别为Nu1，Nu2，…，Nun，则增大因子η分别取为η1=Nu2/Nu1，η2=Nu3/Nu2，…，η(n－1)=Nun/Nu(n－1)．若η ＞ 1表示极限承载压力随该参数增大而增大，反之则表示随该参数增大而减小;若η≈1表示极限承载压力受该参数的影响较小．当改变某个参数时，其它参数不变的固定方式有多种，文中对η在各个数值段的个数n进行统计分析，计算其平均值μη、均方差ση、变异系数δη和mη(mη为η＜1时个数与η＞1时个数的比值)，定性反映极限承载力随该参数的变化趋势．

1)λ对极限承载力Nu的影响．图3为Nu随λ变化的典型情况及λ变化时其增大因子η的统计直方图．由图3可以看出:①随着λ的增大，Nu减小，特别是相对偏心距越小Nu减小越显著;②增大因子η的值均小于1，其均值 μη=0．84，均方差 ση=0．035，变异系数 δη=0．042，mη=240∶0．

图3 N u随λ典型变化情况及λ变化时η的统计直方图Fig．3 The typical relationship of N u－λ and the histogram of n－η whenλ changes

2)e对极限承载力Nu的影响．图4为Nu随e变化的典型情况及e变化时其增大因子η的统计直方图．由图4可以看出:①随着e的增大，Nu减小，当相对初始偏心距较小时Nu减小显著;当相对初始偏心距较大时Nu减小平缓，且增大混凝土强度对Nu的提高影响不大;②增大因子η的值均小于1，其均值μη=0．70，均方差 ση=0．057，变异系数 δη=0．081，mη=256 ∶0．

图4 N u随e的典型变化情况及e变化时η的统计直方图Fig．4 The typical relationship of N u－e and the histogram of n－η when e changes

3)fc对极限承载力Nu的影响．图5为Nu随fc变化的典型情况及fc变化时其增大因子η的统计直方图．由图5可以看出:①随着fc的增大，Nu增大，相对初始偏心距较小时，增大混凝土强度对提高Nu影响明显，而相对初始偏心距较大时，增大混凝土强度对提高Nu影响不明显;②增大因子η的值均大于1，其值 μη=1．06，均方差 ση=0．033，变异系数 δη=0．031，mη=0∶240．

图5 N u随f c的典型变化情况及f c变化时η的统计直方图Fig．5 The typical relationship of N u－f c and the histogram of n－η when f c changes

4)ρ对极限承载力Nu的影响．图6为Nu随ρ变化的典型情况及ρ变化时其增大因子η的统计直方图．由图6可以看出:①随着ρ的增大，Nu近似随ρ线性增大;②增大因子η的值均大于1，其均值μη=1．13，均方差 ση=0．057，变异系数 δη=0．05，mη=0∶240．

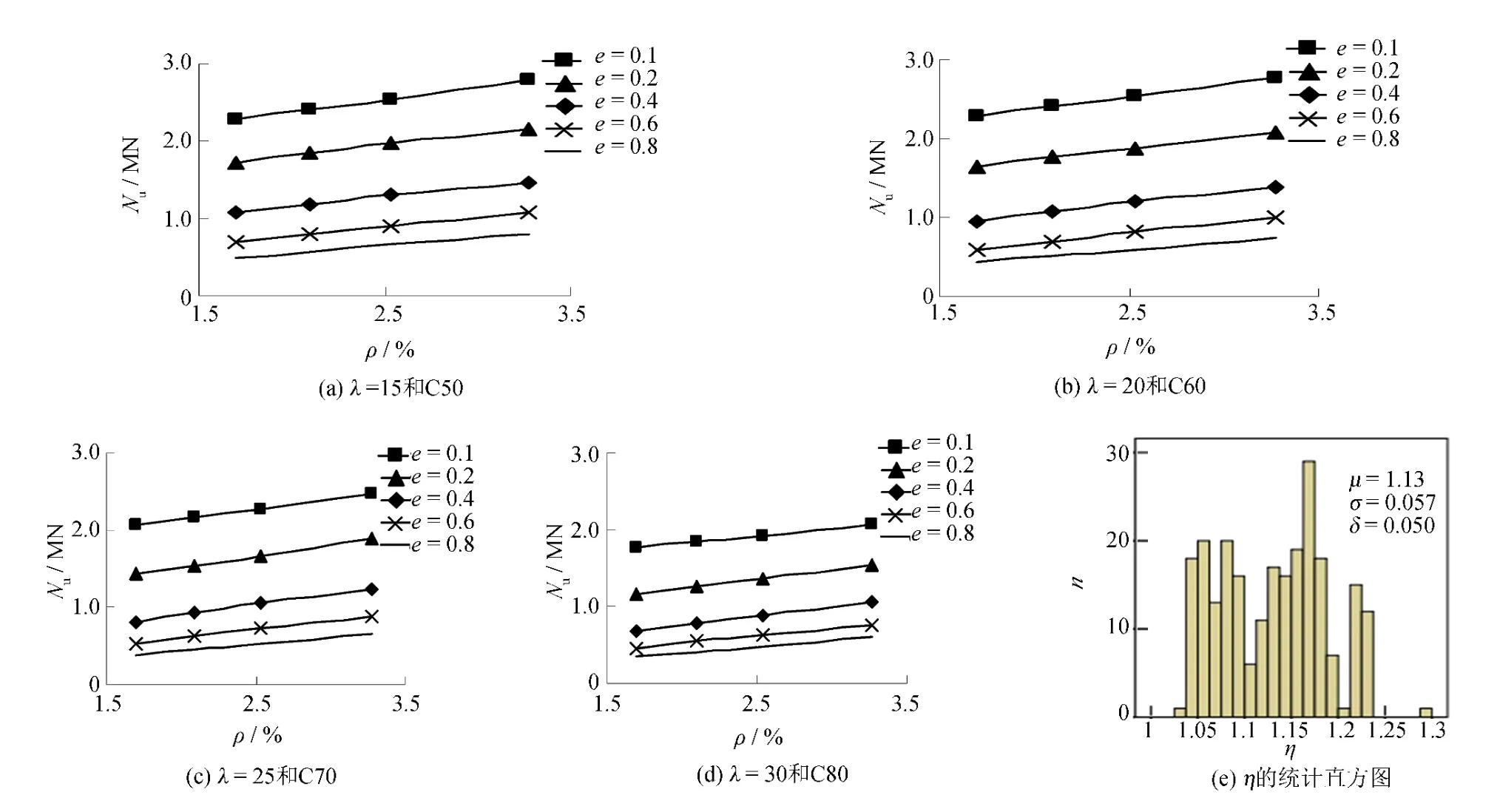
图6 N u随ρ的典型变化情况及ρ变化时η的统计直方图Fig．6 The typical relationship of N u－ρand the histogram of n－η whenρchanges

3 偏压中长柱极限承载力敏感因素分析

为了解钢筋高强混凝土偏压中长柱极限承载力Nu对各影响因素的敏感程度，进行因素方差分析［13］．各因素对Nu影响的方差分析结果如表3所示．由表3可知，对钢筋混凝土偏压中长柱极限承载力Nu的影响敏感性因素依次为:e、λ、ρ和fc．由此可见偏压中长柱的承载力设计不可忽视构件长细比的影响，即刚度影响．

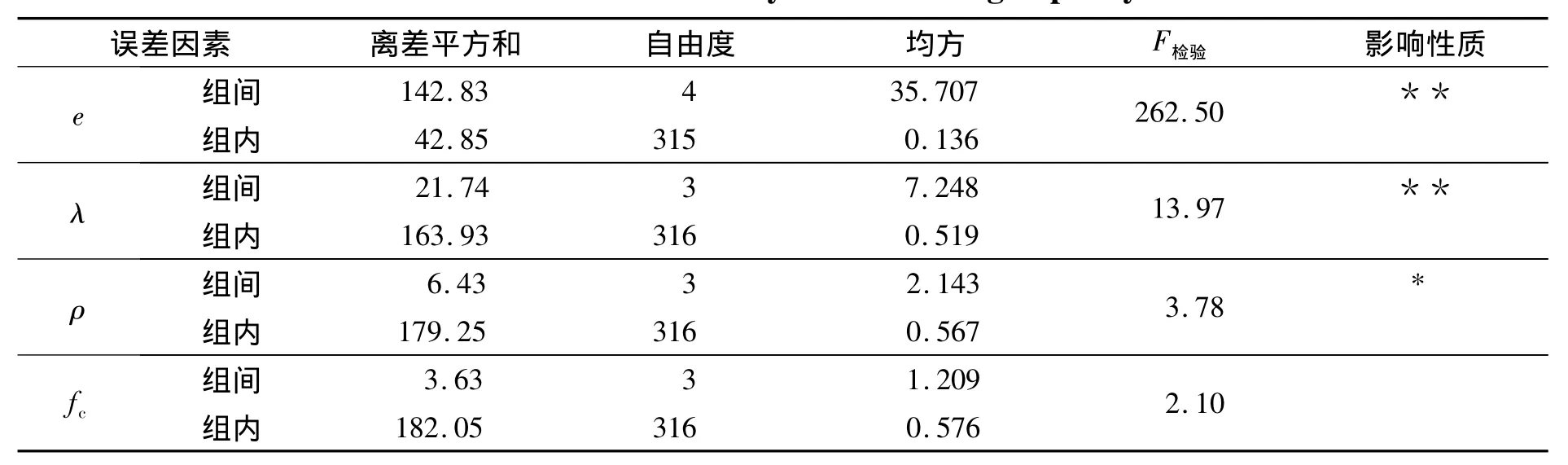
表3 各因素对N u影响方差分析Tab．3 Variance analysis for bearing capacity

4 偏压中长柱承载力的计算公式

通过对表2中所列工况计算结果进行统计分析，得到两端铰接等初始偏心距钢筋混高强凝土偏压中长柱极限承载力Nu的回归计算式为:

式中:a1、a2、a3、a4、a5、a6和a7为常系数，其值见表4．按式(2)对表2中所列320种工况计算的Nu和数值计算的Nu之比的平均值为0．980 5，均方差为0．042 2，变异系数为0．043 1．

式(2)适用条件:①只针对两端铰接等初始偏心距时偏压中长柱的计算数据拟合得到，其它约束或初始偏心距不等的情况不适用;② 只适用混凝土C50、C60、C70、C80，其它强度混凝土尚应研究补充;③计算仅对初始偏心距不大于0．8 h的情况可用，偏心距过大情况有待补充;④计算仅对h/b=4∶3的情况可用，其它情况有待完善．

表4 拟合系数Tab．4 The fitting coefficients

5 结语

通过大量的钢筋高强混凝土偏压中长柱极限承载力数值计算，分析了多个主要影响因素对钢筋高强混凝土偏压中长柱极限承载力的影响情况，经回归给出钢筋高强混凝土偏压中长柱极限承载力与主要影响因素之间的计算公式．研究得到以下结论:

1)钢筋高强混凝土偏压中长柱极限承载力的主要影响因素依次是e、λ、ρ和fc．

2)e对钢筋高强混凝土偏压中长柱极限承载力影响最敏感．随着e的增大，Nu减小．当相对初始偏心距较小时Nu减小显著;当相对初始偏心距较大时Nu减小平缓，且增大混凝土强度对Nu的提高影响不大．

3)λ对钢筋高强混凝土偏压中长柱极限承载力影响不容忽视．随着λ的增大，Nu减小．特别是相对偏心距越小Nu减小越显著．因规范［11］没有给出具体的设计方法，建议对该类柱的设计应特别谨慎．

4)增大纵筋配筋率和混凝土强度对Nu的提高有一定效果．

［1］张光玮．重庆大剧院细长柱试验研究［D］．重庆:重庆大学，2006．

［2］张健，张勋斌，陈滔，等．重庆大剧院细长框架柱承载力非线性分析［J］．重庆建筑大学学报，2008，30(2):108－112．

［3］刁波，叶英华．任意截面钢筋混凝土偏压构件非线性稳定性分析的简化法［J］．北方交通大学学报，1999，23(1):24－29．

［4］魏巍，刘毅，白绍良．钢筋混凝土偏压杆件非弹性稳定的极限承载力分析［J］．重庆建筑大学学报，2000，22(s):80－86．

［5］蒋秀根，剧锦三．偏心受压钢筋混凝土长柱承载力分析［J］．中国农业大学学报，2002，7(2):89－93．

［6］薛建阳，刘锦禄，马辉，等．型钢再生混凝土长柱恢复力模型的试验研究［J］．工业建筑，2013，43(486):35－39．

［7］王卫华，刘阳，徐玉野．初偏心对钢筋混凝土柱受压承载力的影响:铰接［J］．广西大学学报:自然科学版，2014，39(1):81－87．

［8］石立彬．钢筋混凝土细长柱结构在中震作用下若干问题研究［J］．建筑结构，2011，41(5):89－92．

［9］王依群，许贻懂．偏心受压圆截面钢筋混凝土细长柱的计算［J］．天津大学学报，2012，45(2):173－177．

［10］焦俊婷，叶英华，刁波．不规则截面钢筋混凝土梁柱单元模型及应用［J］．哈尔滨工业大学学报，2008，40(4):636－639．

［11］中华人民共和国住房城乡建设部．GB50010－2010混凝土结构设计规范［S］．北京:中国建筑工业出版社，2010．

［12］Diao Bo，Ye Yinghua．Strength analysis of reinforced concrete columns with arbitrary cross－section under bieccentric loadings［J］．Progress in Natural Science，2001，11(4):309－315．

［13］袁志发，周静芋．试验设计与分析［M］．北京:高等教育出版社，2000．