环境参数对公路隧道烟气蔓延影响的实验研究

吴婧，沈斐敏

(福州大学土木工程学院，福建福州 350116)

隧道是为满足交通运输需求及地形而设计的特殊空间，呈现出密闭化、地下化等特性，一旦发生火灾，将出现温度上升快、烟气积累多、人员疏散慢等问题，造成的人员伤亡主要是由火灾所产生的高温和浓烟扩散所引起．随着火灾规模以及通风速度的变化，隧道内的温度以及烟气流动的分布也将发生相应的变化［1］．国内外很多学者对隧道火灾进行了数值模拟分析，如临界风速［2－4］、通风仿真［5－6］、排烟方案［7］、隧道内温度场分布［8－9］等．但是，关于隧道内环境温度、风速对火灾蔓延和烟气扩散影响的研究较少，本文重点讨论环境温度、风速对火灾蔓延和人员疏散的影响，得出隧道火灾预防和控制的一些规律，为监督管理部门对隧道内温度的控制和风速的调节提供参考．

1 隧道模型的建立

1．1 隧道的基本情况

福州象山隧道是福州市二环路上位于西环北路的交通要塞，也是二环上的最大堵点之一．道路等级为城市主干道I级，设计行车速度50 km·h－1，现为四洞连拱结构，中间两洞通行机动车，双向4车道，单洞隧道限界宽9．25 m，车道宽7 m，拱顶高7 m，净空高5 m，隧道全长230 m，距隧道出入口50 m处两洞间设置横通道，高峰时段车流量为4 200辆·h－1．

1．2 隧道模型

所使用的隧道模型(取着火部分隧道)尺寸为9 000 mm×1 500 mm×1 500 mm的有机玻璃模型，有机玻璃模型便于观察烟气流动．实验采用缩尺温度模型［10］，模拟不同火灾强度下，油池火的燃烧特性．根据无量纲控制方程分析(见式1)，采用密度修正弗诺德准则Fr［11－13］，只要保证Re≥0．5×104和瑞利数Ra≥8×106，流动和热力进入自模拟区，实现模型与原型相似［14－15］．

式中:u为特征速度，取浮射流出口速度，m·s－1;L为特征尺寸，取浮射流出口直径，m;g为重力加速度，m·s－2;T为特征温度，取浮射流出口温度，K;ΔT为特征温差，取浮射流出口温度与环境温度的差值，K．

受实验模型材料最高温度及安全因素限制，取温差比尺CΔT=0．079 1，几何比尺CL=0．214，可以确定温度比尺 CT为0．396，速度比尺 Cu为0．207．

对于燃烧区域烟气的流动、热力参数，不是本次实验的重点，而是需要关注扩散区域内热力参数的变化．根据辛烷(汽车燃油主要成分)燃烧化学反应方程式及能量守恒，可得到相应的燃烧参数(表1)作为隧道火源原型数据，将火源模化为热源诱导的高温浮射流．热源原型参数与模型参数对照如表1所示．

表1 热源原型参数与模型参数对照Tab．1 Comparisons between heat prototype parameters and model parameters

2 实验工况设置

2．1 实验系统

模型实验台由热源模拟系统、垂直风流模拟系统和测量系统三部分组成．热源模拟系统采用两级电加热组加热环境空气，直至满足热源风温要求，在热源系统前端添加去离子水烟雾发生器，便于追踪观察，烟雾和加热空气在热风箱(31．0 cm×15．5 cm×22．5 cm)里混合后在浮升力作用下进入实验隧道．为保证垂直风流送风均匀，在隧道的进风断面设置了配有均流板的轴流式风机，并采用变频器进行风速调节．实验测量以地下工程安全数字化实验系统为平台，系统包括两大部分:一是硬件部分，负责监测数据采集，安装有JWSK－6温湿度传感器4个、SBWZ铂热电阻传感器12个、EE65微风风速传感器8个、风杯式风速传感器(自研)2个、SN－687PTA/26W工业摄像头2个、DH－DVR0404LE－AS硬盘录像机1台;二是基于WebGIS的安全监测模块，系统可连续监测隧道内风速、温度、湿度等安全参数及图像信息，安全监测系统从空间数据库中得到相关数据，并实现动态显示和分析评价．

2．2 测点布置

根据美国消防协会NFPA发布的有关公路隧道、桥梁和限制通行的高速公路的防灾设计标准(NFPA 502)中的可接受维生环境的准则，当烟气界面下降到人眼特征高度(取为1．6 m)时，对人的危害将是直接烧伤或吸入热气体引起的．结合本实验室的实施条件，布置以下测点，见图1．

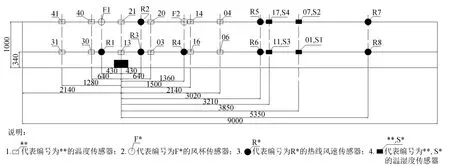
图1 传感器位置布置图Fig．1 Layout plan of sensor position

2．3 实验工况

隧道模型内按汽车建立模型，车辆的最大长、宽、高尺寸分别取4．80 m×1．85 m×1．50 m，着火车辆为一辆，其位置设在距隧道入口2．14 m(对应隧道原型为距离隧道入口55 m)处，着火点向隧道入口方向发生堵车，着火点向隧道出口方向无车停留．实验工况如表2所示．

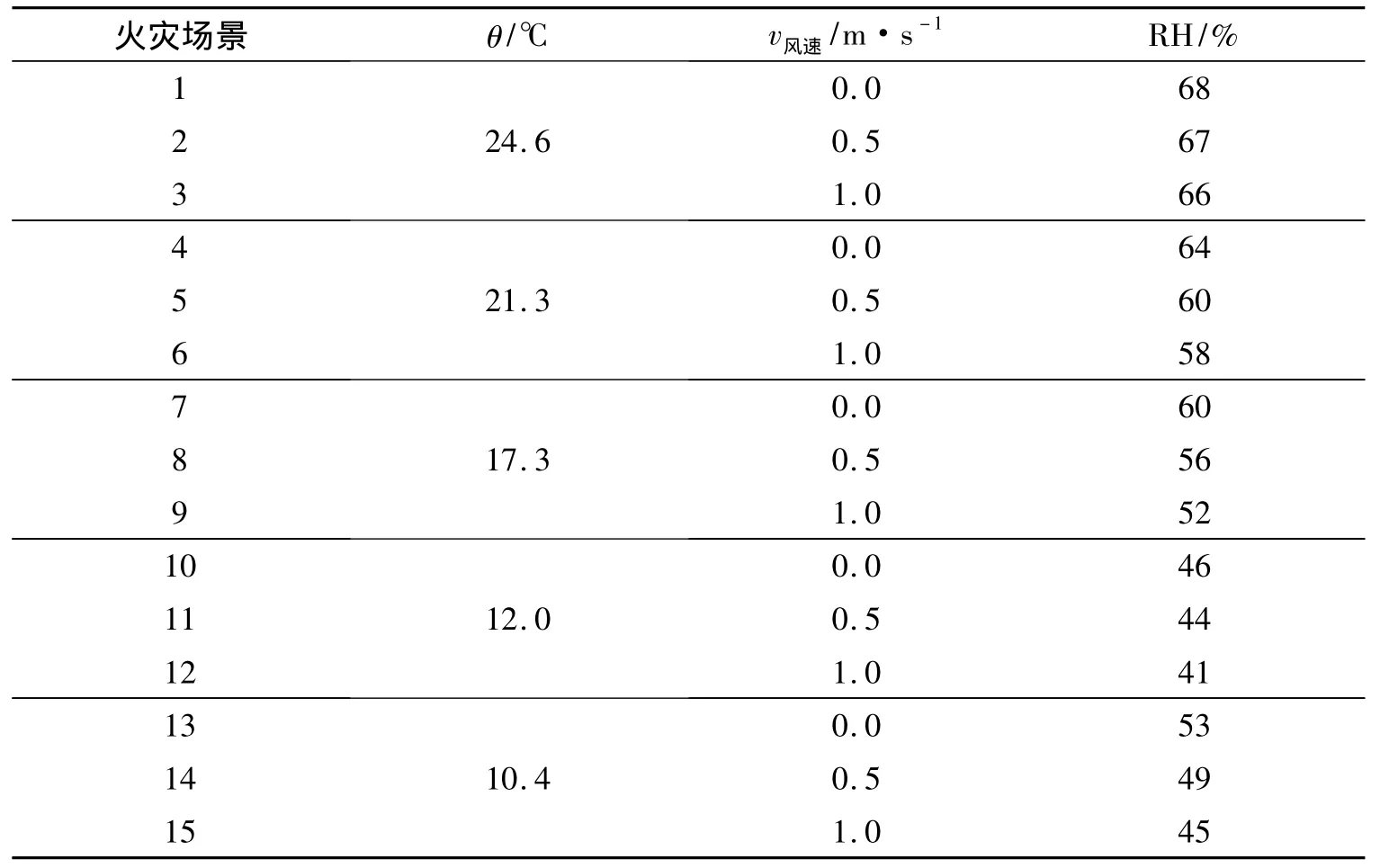
表2 实验工况设置Tab．2 Experimental conditions setting

2．4 实验结果

实验采用控制变量法，以隧道内初始温度、风速、湿度为变量，得出目标点处的温度随烟气蔓延时间的变化过程，并根据相似理论对模型实验数据进一步折算为原型隧道烟气速度、温度的变化，据此讨论热烟气蔓延的规律．

2．4．1 隧道顶部测点温度变化结果

当环境温度为17．3℃时，火源上方隧道顶部测点21及火源前方0．64 m(对应隧道原型为火源前方3 m)处隧道顶部测点20在三种不同风速下(隧道模型中v0=0 m·s－1，v1=0．5 m·s－1，v2=1 m·s－1;对应隧道原型中 v0=0 m·s－1，v1=2．4 m·s－1，v2=4．8 m·s－1)的温度变化情况见图2、3 所示．

图2测点21在不同风速下温度值Fig．2 Temperature values of measuring point 21 under different wind speeds

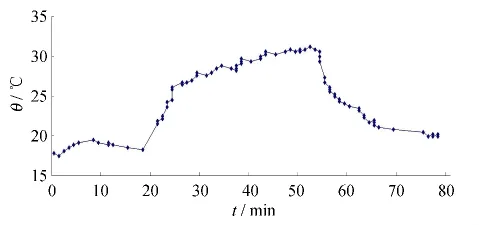
图3 测点20在不同风速下温度值Fig．3 Temperature values of measuring point 20 under different wind speeds

图2中，前25 min未发生火灾，温度保持不变，第25 min火源点燃持续35 min并处于无机械通风状态，最高温度可达到44．53℃(根据相似理论折算成原型隧道温度为361．55℃)，当开启风机并保持0．5 m·s－1的风速15 min时，温度快速下降至21．97℃(折算后温度为76．34℃)，再调大风速至1．0 m·s－1并保持18 min，温度继续下降至19．30℃(折算后温度为42．58℃)．

图3中，第20 min火源点燃持续燃烧33 min并处于无机械通风状态，温度缓慢上升到最高温度31．17℃(折算后温度为194．89℃)，开启风机并保持0．5 m·s－1的风速10 min时，温度快速下降至22．27℃(折算后温度为80．94℃)，再调大风速至1．0 m·s－1温度下降到19．89℃(折算后温度为50．46℃)．

目前，计算火源上方顶棚射流最高温度的理论分析主要有Alpert公式［16－17］和Kurioka［18］模型．Kurioka模型对于纵向风速为0或风速很小的情况，Fr值趋近于0，其预测结果与真实情况差别很大［8］．Alpert等通过烟气羽流撞击顶棚实验得到下列关于最高温度θmax(℃)的分布关系式:

式中:θ0为环境温度，℃;h为火源底面到顶棚的高度，m;y为顶棚射流在水平方向上离火源中心线的距离，m;Q为热释放率，kW．

用Alpert公式对实验数据进行验证，对火源上方隧道顶部测点21、20的最高温度进行计算，取:

θ0=17．3 ℃，h=7 －0．2=6．8 m，Q=12 MW，y ＜0．18 h=1．2，θmax－ θ0=362．88 ℃，θmax=380．18 ℃;

y ＞0．18 h=1．2，θmax－ θ0=199．36 ℃，θmax=216．66 ℃;

计算值与测点21、20测得的最高温度值361．55、194．89℃接近，误差分别为4．90%和10．04%，可见Alpert公式计算火源上方最高温度的方法是可靠的，实验测得的数据也具有可靠性．同时，火源前方1．5、2．1、3．2、3．8 m(对应隧道原型为火源前方7、10、15、18 m)处隧道顶部测点14、04、17、07 在三种不同风速下(隧道模型中 v0=0 m·s－1、v1=0．5 m·s－1、v2=1 m·s－1，对应隧道原型中 v0=0 m·s－1、v1=2．4 m·s－1、v2=4．8 m·s－1)的温度变化情况见图4～图7所示．从图4～7可以看出，随着离火源距离越远，隧道顶部温度上升幅度越小，最高温度也随之降低，并且开启风机通风对温度影响也不大．

同一条件下，火源后方0．64、1．28 m(对应隧道原型为火源后方3、6 m)、火源前方1．5、2．1 m(对应隧道原型为火源前方7、10 m)处隧道侧壁人眼特征高度处测点30、31、16、06在三种不同风速下(隧道模型中 v0=0 m·s－1、v1=0．5 m·s－1、v2=1 m·s－1，对应隧道原型中 v0=0 m·s－1、v1=2．4 m·s－1、v2=4．8 m·s－1)的温度变化情况见图8～图11所示．

图8中，第20 min火源点燃持续燃烧33min并处于无机械通风状态，温度缓慢上升到最高温度20．51℃(折算后温度为57．88℃)，开启风机并保持0．5 m·s－1的风速10 min时，温度快速下降至20．21℃(折算后温度为54．09℃)，再调大风速至1．0 m·s－1温度下降到18．16℃(折算后温度为28．17℃)．

图4 测点14在不同风速下温度值Fig．4 Temperature values of measuring point point 14 under different wind speeds

图5 测点04在不同风速下温度值Fig．5 Temperature values of measuring 04 under different wind speeds

图6 测点17在不同风速下温度值Fig．6 Temperature values of measuring point 17 under different wind speeds

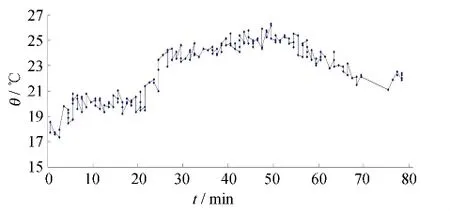
图7 测点07在不同风速下温度值Fig．7 Temperature values of measuring point 07 under different wind speeds

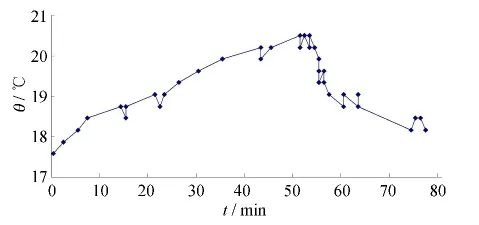
图8 测点30在不同风速下温度值Fig．8 Temperature values of measuring point 30 under different wind speeds

图9 测点31在不同风速下温度值Fig．9 Temperature values of measuring point 31 under different wind speeds

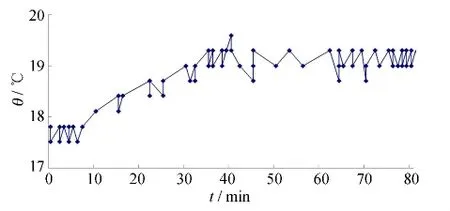
图10 测点16在不同风速下温度变化值Fig．10 Temperature values of measuring point 16 under different wind speeds

图11 测点06在不同风速下温度变化值Fig．11 Temperature values of measuring point 06 under different wind speeds

图9中，第20 min火源点燃持续燃烧35 min并处于无机械通风状态，温度缓慢上升到最高温度19．04℃(折算后温度为39．30℃)，开启风机并保持0．5 m·s－1的风速15 min时，温度快速下降至18．46℃(折算后温度为31．96℃)，再调大风速至1．0 m·s－1温度下降到18．16℃(折算后温度为28．17℃)．

从图8～11可以看出，随着离火源距离越远，隧道侧壁人眼特征高度处温度上升幅度越小，最高温度也随之降低．

2．4．2 烟气蔓延的时间

在表2中列出的15个场景工况下烟气蔓延到达目标点的时间如表3所示．

表3 各场景下烟气蔓延到达特定位置的时间Tab．3 Smoke spread time to reach the particular locations in experimental conditions (s)

由表3实验数据知，环境温度越低，烟气蔓延时间越短．产生这种现象的原因是:隧道内发生火灾后，火场温度升高，空气膨胀、体积增大、密度减小，与隧道外的冷空气产生较大的密度差，引起热空气向上运动，即“烟囱效应”和“浮力效应”的综合作用．外界环境温度越低，这种密度差越大，热压越明显，烟气蔓延速度会加大，传播时间就会缩短．

2．4．3 烟气蔓延的过程

当环境温度为10．4℃，无风工况时，火源燃烧后，热烟气迅速撞击顶棚并向四周扩散，然后在模型的上部空间逐渐积累并向上、下游蔓延，烟气层在传播过程中基本保持水平，下沉速度缓慢，传播时间较长，如图12所示．风速较小时(模型中v=0．5 m·s－1，原型中v=2．4 m·s－1)，火源燃烧后产生的烟气上升后，被轴流风机的气流打散，烟气逐渐弥漫整个隧道空间，并向下游扩散，上游无明显烟气流，见图13．风速较大时(模型中v=1．0 m·s－1，原型中v=4．8 m·s－1)，火源燃烧后，产生的烟气还未上升，就被轴流风机的气流吹散，烟气迅速弥漫整个隧道空间，向下游扩散，上游无烟气流，见图14．

图12 无风时烟气蔓延分布图Fig．12 Smoke spread distribution under no wind

图 13 v=0．5 m·s－1时烟气蔓延分布图Fig．13 Smoke spread distribution under wind speed is 0．5 m·s－1

图14 v=1 m·s－1时烟气蔓延分布图Fig．14 Smoke spread distribution under wind speed is 1m·s－1

3 结语

1)隧道内发生火灾后，火源上方隧道顶部的温度上升幅度大，响应时间短，其最高温度的测量值与Alpert公式理论计算的结果比较接近，可以用Alpert公式计算预测隧道内火源上方的最高温度值;火源上、下游人眼特征高度处温度的上升幅度较小，离火源距离越远，火源对其上、下游的影响逐渐减小，因此火灾发生后，350 s内不应开启风机，此时烟气蔓延还未降至人眼特征高度处，且此高度以下温度变化幅度小，离火源较远的人员可以逃生．

2)通风对隧道内温度的影响很大，火灾发生后，隧道内火源附近温度急剧上升，开启风机通风后，温度迅速下降，但是并不是风速越大，温度下降的越多，而且离火源距离越远，通风对温度影响越小，因此火灾发生后，350 s后应开启风机通风，可迅速降低隧道内温度，但风速不宜大于3 m·s－1．

3)根据烟气蔓延时间及人的步行速度(约为1．2 m·s－1)，对于特长或交通量比较大的隧道，隧道内每隔300～400 m应设置避难联络横通道．

4)环境温度较低时，烟气蔓延时间更短，在低温时段应为人员安全疏散及灭火救援争取更多时间．

［1］何凯明．隧道火灾数值模拟及人员疏散安全性研究［J］．交通标准化．2010，222(11):36－38．

［2］Kennedy W D，Parsons B．Critical velocity:past，present and future［C］//One Day Seminar of Smoke and Critical Velocity in Tunnels．London:ITC，1996:305－322．

［3］Wu Y，Bakar M Z A．Control of smoke flow in tunnel fires using longitudinal ventilation systems:a study of the critical velocity［J］．Fire Safety Journal，2000，35(4):363 －390．

［4］Hwang CC，Edwards JC．The critical ventilation velocity in tunnel fire－a computer simulation［J］．Fire Safety Journal，2005，40(3):213－244

［5］Friedman R．An international survey of computer models for fire and smoke［J］．Journal of Fire Protection Engineering，1992，4(3):81－92．

［6］Chow W K．Simulation of tunnel fire using a zone model［J］．Tunnelling and Underground Space Technology，1996，11(2):221－236．

［7］Chow WK．On smoke control for tunnels by longitudinal ventilation［J］．Tunnelling and Underground Space Technology，1998，13(3):271－275．

［8］毛军，郗艳红，樊洪明．隧道内火焰顶棚射流最高温度的分布研究［J］．中国矿业大学学报，2010，39(3):346－351．

［9］彭伟，霍然，胡隆华，等．隧道内纵向风速对火源上方烟气温度影响的试验［J］．中国科学技术大学学报，2006，36(10):1 063－1 068

［10］Vauquelin O，Mégret O．Smoke extraction experiments in case of fire in tunnel［J］．Fire Safety，2002，37(5):525 －33

［11］科纳科夫．相似理论及其在热工上的应用［M］．李德桃，贺道德，译．北京:科学出版社，1962．

［12］诺吉德．相似理论及因次理论［M］．官信，译．北京:国防工业出版社，1963．

［13］基尔皮契夫 M B．相似理论［M］．沈自求，译．北京:科学出版社，1955．

［14］章熙民，任泽霈，梅飞鸣．传热学［M］．北京:中国建筑工业出版社，2001．

［15］米海耶夫M A．传热学基础［M］．王补宣，译．北京:高等教育出版社，1954．

［16］Alpert R L．SFPE hand－book of fire protection engineering:ceiling－jet flows［M］．Massachusetts:National Fire Protection Association，1995:233－246．

［17］Hasemi Y，Tokunaga T．Some experimental aspects of turbulent diffusion flames and buoyant plumes from fire sources against a wall out in a corner of walls［J］．Combustion Science and Technology，1984，40(1):1 －17．

［18］Kurioka H，Oka Y，Satoh H，et al．Fire properties in near field of square fire source with longitudinal ventilation in tunnels［J］．Fire Safety Journal，2003，38(4):319 －340．