两阶段抽样法在无标度网络结构特征量估计中的应用

邓光明，苏 健，陈玟宇，贾 贞

(1.桂林理工大学 理学院；2.广西空间信息与测绘重点实验室,广西 桂林 541004)

0 引言

无标度网络是由美国圣母大学的Barabási和Albert在1999年提出的一个重要网络模型[1，2]，他们在研究了电力网络和线粒虫神经网络的统计时发现这些网络的度分布均可用幂律分布来描述，称此性质为无标度特性。其后的许多研究发现，许多网络都具有无标度特性，如Internet、WWW、科研合作网络、在线社交网络等等。无标度网络的主要特性是其度分布极不均匀，其少数节点具有很高的度，多数节点的度很低，而这些少数度高的节点（在技术网络中也称为hub节点）在网络中却十分重要，对网络中病毒或信息的传播具有举足轻重的作用。对这类无标度网络的抽样，若采用随机抽样法可能导致入样的节点均为度低的节点，忽略了度高的节点；若采用滚雪球抽样法、广度优先算法、随机游走等抽样方法，则会导致样本网络中的节点偏向于度高的节点，而忽略了度低节点，这样获得的样本网络难以估计完全网络的真实特征。本文对上述抽样方法进行改进，针对BA无标度网络的度分布不均匀特性，设计一种改进的两阶段抽样方法[3，4]。用此方法进行抽样，使得原始网络中的高度节点和低度节点都以一定比例入样，因此能根据网络的结构特点控制不同度的节点的入样率，从而所得到的样本网络能更好地估计完全无标度网络的结构特性。

1 两阶段抽样方法

由于BA无标度网络中大部分节点为低度节点，为了避免抽样时仅抽到低度的节点，而忽略了网络中具有重要地位的高度节点，本文提出使用两阶段抽样法，将低度节点和高度节点都以一定比例选入样本网络，具体算法如下：

第一步，在规模为N的初始网络G中不重复随机抽取ρN个节点为第一阶段抽样，其中ρ为第一阶段抽样率，得到的样本记为样本Ⅰ；

第二步，在样本Ⅰ中随机取δρN个节点进行向前一步随机游走，得到新的δρN个节点作为样本Ⅱ，这为第二阶段抽样；

第三步，将样本Ⅰ与样本Ⅱ节点合并为为两阶段抽样的样本节点，加上这些节点之间的原始边，即得到两阶段抽样的样本网络Gs，样本容量不超过(1+δ)ρN。

根据此算法可知，样本Ⅰ代表网络中度较低的节点。根据Cohen等[5]提出的，在给定网络中，沿着随机选择的一条边到达某特殊节点的概率与此特殊节点的度数成正比，度越高的节点选入样本Ⅱ的概率越大，因此样本Ⅱ代表网络中度较高的节点。所以，低度节点入选的比例约为ρ，高度节点入选的比例约为δρ。我们可以用参数ρ和δ来控制两类节点的入样率。由于样本Ⅱ的节点是原节点进行向前一步随机游走得到的节点，因此样本Ⅱ的节点可能为ρN个节点外的节点，也可能是样本Ⅰ中的节点，即有少数节点可能被重复抽中，因此最终得到的样本的样本量n≤(1 +δ) ρN 。

2 网络的生成与结构参量

2.1 初始BA无标度网络的生成

初始网络为BA无标度网络，其构造算法[6]为：

（1）增长：从一个具有m0个节点的连通网络开始，每次引入一个新的节点并且连到m个已存在的节点上。

（2）优先连接：一个新节点与一个已存在的节点i相连接的概率∏i与节点i的度ki之间满足如下关系

根据上述算法，本文生成3个初始网络 G1，G2，G3，取每个网络的网络规模N=10000，m0=100，m分别取m=20，m=50，m=80。m越大初始网络中，节点的平均度越大，且相比于m较小的初始网络，其度小的节点数越少。

2.2 网络的结构特征量

本文选取下面三个典型的网络结构特征量来进行样本估计并评价估计结果。

（1）幂率度分布：完全BA无标度网络的度分布是服从幂率分布的[7,8]，即度分布具有形式 P(k)～k-γ，其中 P(k)是度为k的节点的经验概率，也就是网络中一个随机选择的节点的度为k的概率，γ＞0为幂指数，许多实际的无标度网络的幂指数一般介于2与3之间，网络的度分布图在双对数坐标下大致呈线性形式。下文中我们将进行抽样模拟，用样本网络来估计完全网络的幂率度分布的幂指数。

（2）聚类系数：网络的聚类系数C定义为：

（3）节点度相关性：网络的度相关性是衡量网络中任意两个节点之间连边概率是否与这两个节点的度值有关的指标。一般地，网络的度相关性可以使用图形来描绘，即在双对数二维坐标中绘制度为k的节点的相邻节点的平均度数knn随k的变化情况。当knn随k的增大而增大时，称网络是度正相关的，即总体上度大的节点倾向于连接度大的节点；当knn随k的增大而减小，则称网络是度负相关的，即度大的节点倾向于连接度小的节点；当knn不随k的变化而显著变化时，称网络不具有度相关性。平均度数knn定义为：

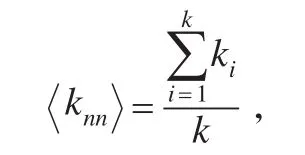
其中ki指的是度为k的节点的第i个邻居节点的度。

3 抽样模拟与结果分析

在抽样模拟中，对于每个初始网络，设置抽样率ρ分别为ρ=0.2，ρ=0.5，ρ=0.8高度节点入样控制δ分别取δ=0.2，δ=0.5δ=0.8。考虑到抽样随机因素的影响，对每个初始网络在每一组参数(ρ，δ)下重复抽样50次取平均结果。

图1考察网络的幂率度分布的估计效果。图1（a）—（c）是在固定δ（δ=0.5），而 ρ取不同值，在不同的初始网络中进行抽样的子网络度分布图。图1（d）—（f）是固定ρ（ρ=0.5），而δ取不同值下抽样所得子样本网络的度分布图。从图1可以看出，每个图中的4条线基本都呈平行状态，表明各参数组合下的样本网络都能估计出初始网络服从幂率度分布。我们进下用最小二乘法获得各分布的幂指数的估计值，见表1所示。需要指出的是，通常很难看到在度的整个取值范围内都很好地服从幂律分布的网络，我们提到某个网络具有幂率分布时，往往指的是当度值较大时分布近似具有幂律形式[9]。因此本文估计的是线性部分的幂律指数。结果显示，所有样本的γ值都在2与3之间，能很好地反映初始网络的度分布情况，且随着ρ的增加，样本对幂指数的估计越接近于初始样本。样本网络尾部呈现“波浪”状态，这取决于初始网络的形态。取其它参数组合所得样本的结论一样。总的来说，对于幂率度分布，两阶段抽样能较好地估计初始网络的总体形态，尤其是对网络的中度节点的估计。随着ρ和δ增加，样本网络对幂率度分布的估计效果更好。

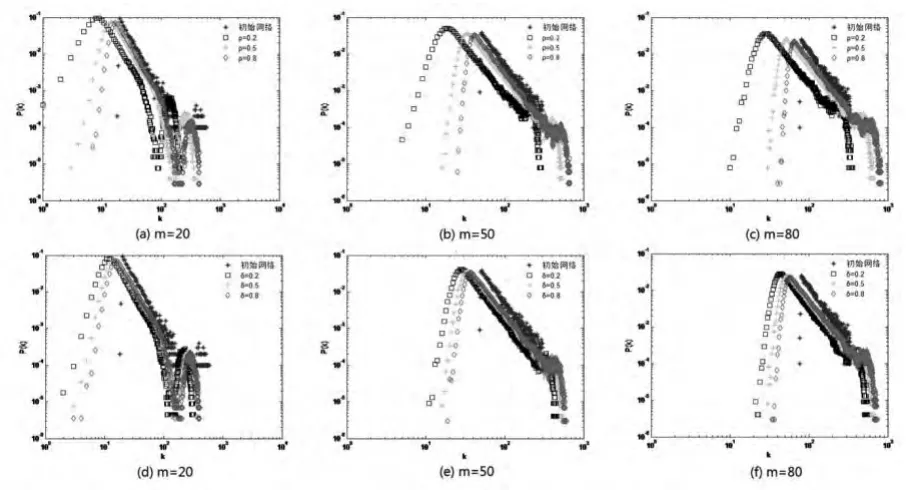
图1 样本网络与初始网络的度分布比较图

图2考察的是聚类系数的估计效果。图2中的星形点为各抽样参数组合(ρ，δ)下在不同的m所对应的初始网络中，抽取的50个样本网络的聚类系数的均值，水平虚线为初始网络的聚类系数。当m=20，50，80时，初始网络的聚类系数分别为：0.0218，0.0296,0.0387，即随着m的增大，初始网络的聚类系数也增大。抽样结果表明，当ρ较小时，随着δ的增加，样本网络会大大高估初始网络的聚类系数；当ρ较大时，样本网络随着δ的增加，其聚类系数则越接近于初始网络的聚类系数，估计效果显著增强。综合来看，提高第一阶段抽样率更有利于样本对初始网络聚类系数的估计，且随着总抽样率的增加，样本网络的聚类系数越接近于初始网络。此外，样本网络的聚类系数都大于初始网络，这是因为两阶段抽样法能使hub节点更易入样，某个节点的任意两个邻居节点的连边概率更高，因此样本网络的聚类系数略高于初始网络的聚类系数。

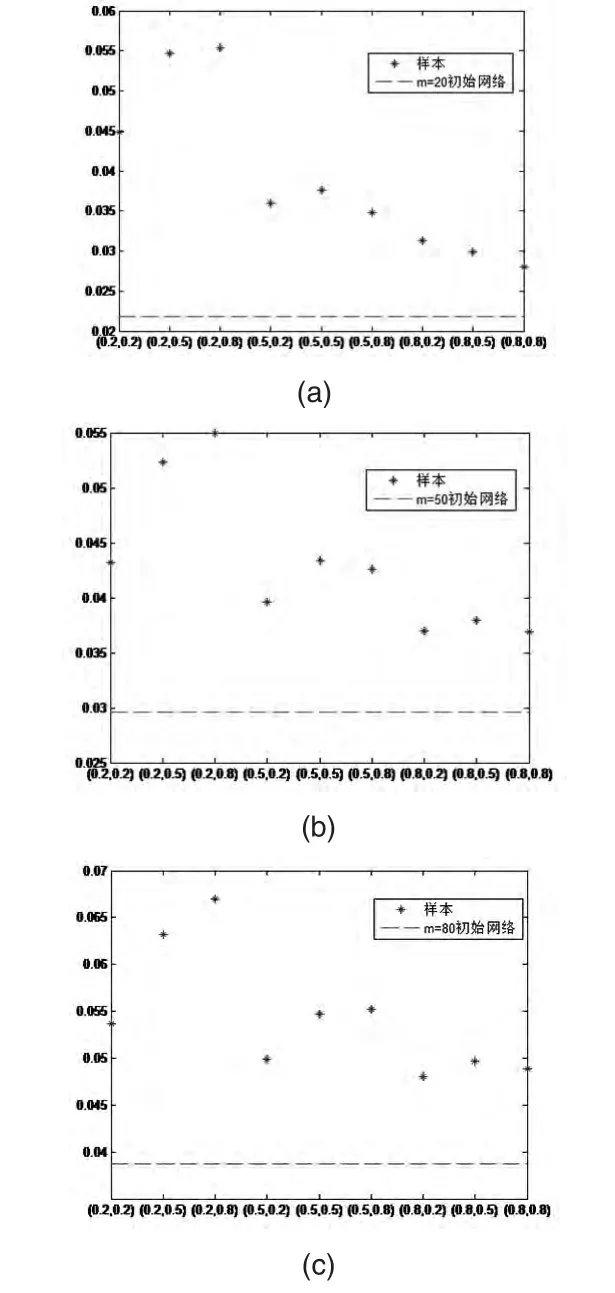
图2 样本网络与初始网络的平均聚类系数比较图

图3考察的是节点度相关性的估计效果。图3（a）—（c）和（d）—（f）分别为 δ=0.5和 ρ=0.5时，不同 ρ和 δ在不同初始网络下得到的样本网络的度相关图。图3显示，3个初始网络的knn都近似常数，即节点的连边概率和节点的度没有明显的正负相关关系。在m=20的初始网络中，knn出现“断层”，表明网络中有部分孤立节点。模拟结果表明，不论何种参数组合下的样本，都能大致估计初始样本不具有度相关性。但样本对初始网络knn值的估计效果对于ρ值的变动较敏感，尤其当ρ=0.2时，样本会大大低估初始网络的knn值，而 ρ=0.5和 ρ=0.8的估计效果相差不大，因此，当考虑抽样成本时，取ρ=0.5便可以得到较好的knn值估计。相比而言，样本对knn值的估计效果对于δ的变动则不是十分敏感。总的来说，两阶段抽样法能较准确地估计初始网络的度相关性，但样本网络的估计值略低于初始网络的knn值。

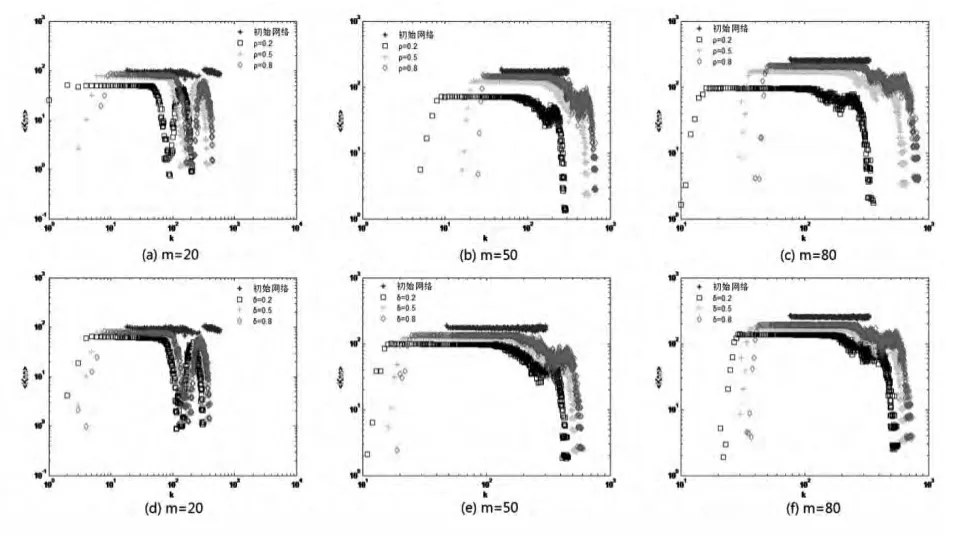
图3 样本网络与初始网络的度相关性比较图

4 样本稳定性评价

方差的大小决定着样本的稳定性，抽样平均误差的大小决定着样本对总体推断结论的准确程度。本文在m=50的初始网络中，计算各参数组合下50个样本网络的幂指数γ的方差和抽样平均误差，用以评价不同参数组合的样本对总体的估计效果。修正样本方差定义为：

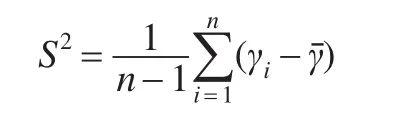
其中n为样本个数，γi为第i个样本网络的幂指数，为50个样本网络的幂指数均值。抽样平均误差定义为：

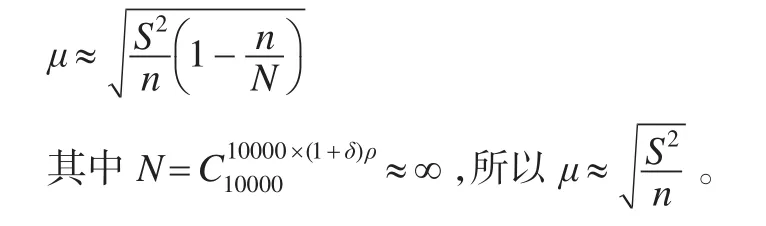
从计算结果（表2）中可以看出，(0.8，0.5)组合下的样本方差和抽样平均误差最小，抽样最稳定，结合表1也看出，该组合下的幂指数估计也较接近初始网络，(0.5，0.8)组合下的样本稳定性次之。评价结果表明，样本的稳定性较好，而且稳定性与样本量的大小呈较明显的正相关关系。实际抽样中，我们可以根据实际条件参照上述估计效果对参数组合(ρ，δ)进行取值。

表2 样本网络的样本方差和抽样平均误差

[1]Barabási A-L,Albert R.Emergence of Scaling in Eandom Networks[J].Science,1999,286(5439).

[2]Barabási A-L:Scale-free Networks:A Decade and Beyond[J].Science,2009,325(5939).

[3]李勇，黄霞，侯志强.两阶段抽样调查的平衡两层次样本轮换研究[J].统计与决策，2009,（19）.

[4]贺建风.基于二阶段抽样的双重抽样框估计量设计[J].统计与决策，2011,（15）.

[5]Cohen R,Havlin S,Avraham D B.Efficient Immunization Strategies for Computer Networks and Populations[J].Physical Review Letters,2003,91(24).

[5]汪小帆，李翔，陈关荣.网络科学导论[M].北京：高等教育出版社，2012.

[6]Albert R,Jeong H,Barabási A-L:Diameter of the World Wide Web[J].Nature,1999,401(6749).

[7]Barabási A-L,Albert R.Emergence of Scaling in Random Networks[J].Science,1999,286(5439).