基于1/3倍频程的轨道动力学测试参量校核

徐中秋

(中国铁道科学研究院研究生部，北京100081)

基于1/3倍频程的轨道动力学测试参量校核

徐中秋

(中国铁道科学研究院研究生部，北京100081)

在轨道动力学测试中所测得的相关参量(如钢轨垂直力和钢轨垂向位移)并不是相互独立的，相关的参量之间可以相互校核来证明试验数据的正确性，同时展示试验数据的可信度。本文利用有限元软件建立轨道模型，并且通过将一实测钢轨垂直力样本的1/3倍频程作为有限元模型的激励谱计算出钢轨垂向位移的理论幅值谱。利用钢轨垂向位移理论幅值谱与钢轨垂向位移实际幅值谱进行配对T检验，根据检验结果对比理论数据与实际数据的差异，校核结果证明钢轨垂直力和钢轨垂向位移的测试数据是正确的。

轨道动力学 有限元 1/3倍频程

轨道动力学测试中所测试的参量如轮轨垂直力和钢轨垂向位移间通常存在相关关系，因此可以对两个相关参量进行相互校核，确保试验数据的正确性。

将信号源发出的振动信号强度按照频率顺序展开，表示成频率的函数，并研究振动能量的变化规律，称为傅里叶频谱分析［1-2］。频谱分析中1/3倍频程分析方法具有谱线少频带宽的特点，它常用于声学、人体振动、机械振动等的测试分析以及频带范围较宽的随机振动测试分析［2］。本文的有限元计算由于所涉及的轮轨力频带范围宽，直接用于频谱计算较为繁琐，所以采用1/3倍频程谱进行有限元谱分析。

1 1/3频程原理

倍频程是频域分析中频率的一种相对尺度，是由一系列频率点和对应这些频率点附近频带内振动信号的平均幅值所构成。平均幅值也就是振动信号的有效值。这些频率点定义为中心频率，中心频率附近有上限频率和下限频率，上下限频率之间的频率范围称为频带宽度，又叫带宽［2-3］。

图1(a)是从厦深铁路联调联试轨道动力学测试数据中选取的垂直力时域波形样本，将垂直力时域波形转换为幅值谱，见图1(b)。将图1(b)的垂直力样本幅值谱转换为1/3倍频程，见图1(c)。

垂直力1/3倍频程各频率数值见表1。

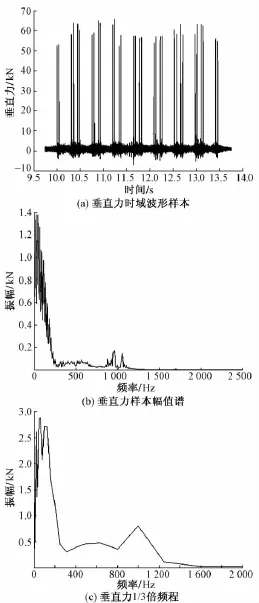
图1 垂直力样本数据分析

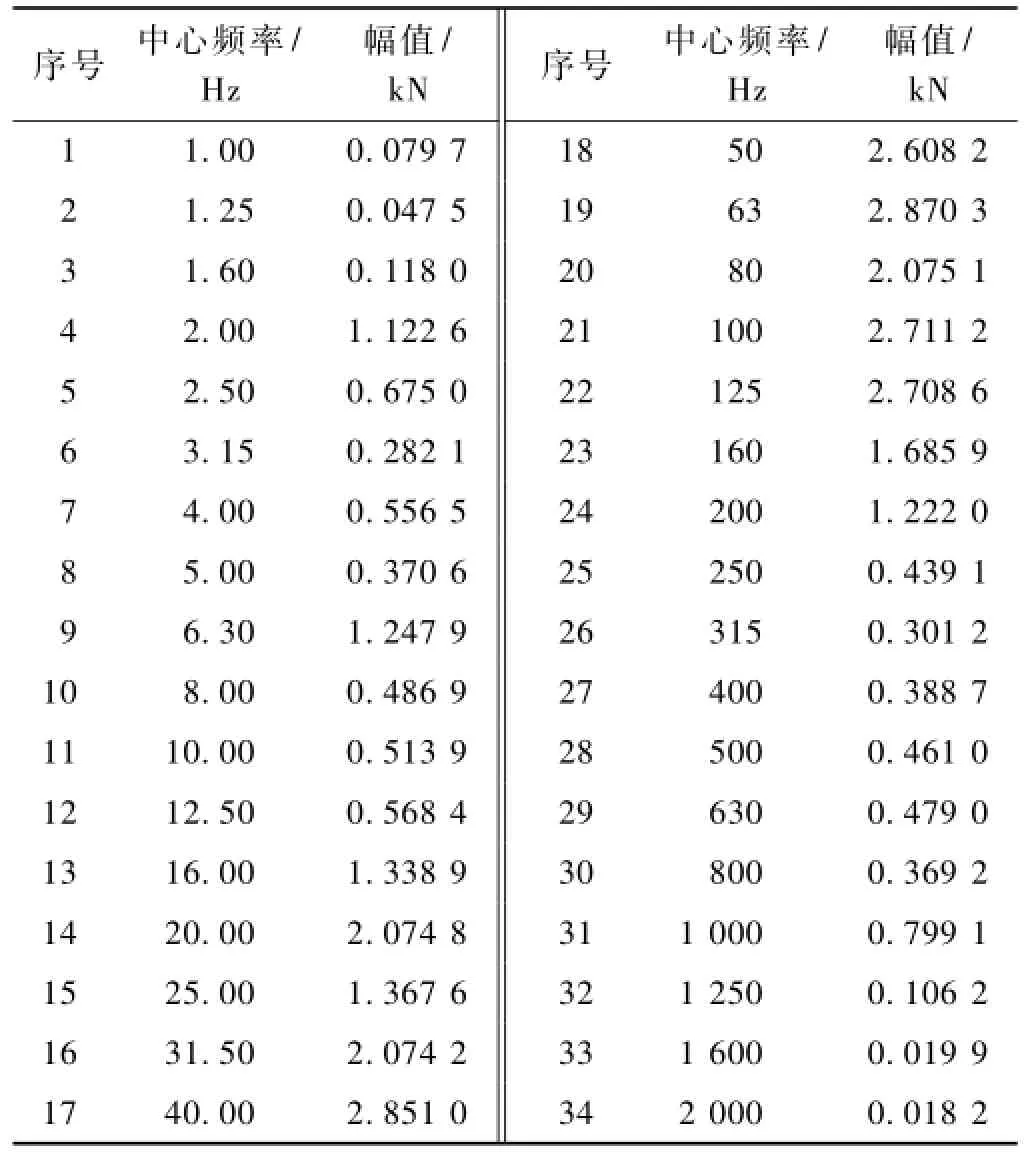
表1 垂直力1/3倍频程

2 轨道测试有限元分析

2.1 计算模型

本文中轨道模型采用连续弹性基础梁模型［4］，所以此次ANSYS有限元模型选用Beam188单元构建钢轨断面，作为梁断面，见图2(a)。轨道扣件采用弹簧模拟［4-6］，模型见图2(b)。

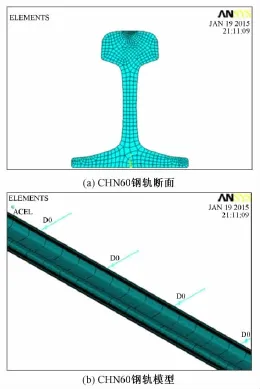
图2 钢轨断面及模型

2.2 谱分析

谱分析是用模态分析结果与已知谱结合进而计算模型的位移和应力的分析技术。谱分析替代时间—历程分析［7］。在有限元计算中代入经1/3倍频程计算得到的位移频率响应频谱，理论位移幅值谱见表2，其波形见图3(a)。试验中所测得的钢轨垂向位移时域波形见图3(b)。将试验所测得的位移时域波形转化成位移幅值谱，见图3(c)。

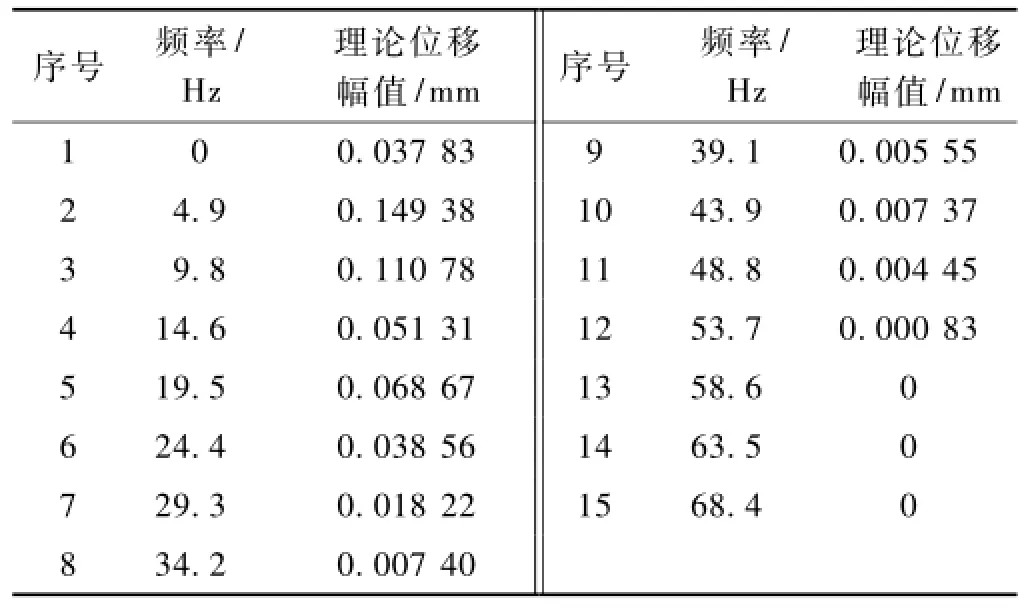
表2 理论位移幅值谱

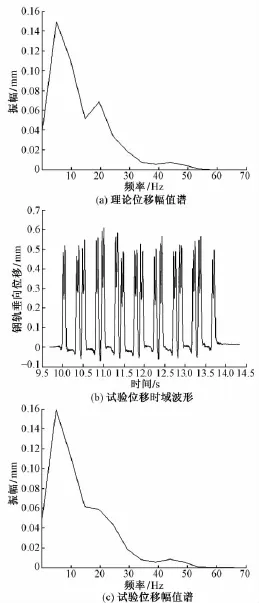
图3 位移幅值谱分析

试验所测得的位移幅值谱和理论计算位移幅值谱对比见表3。

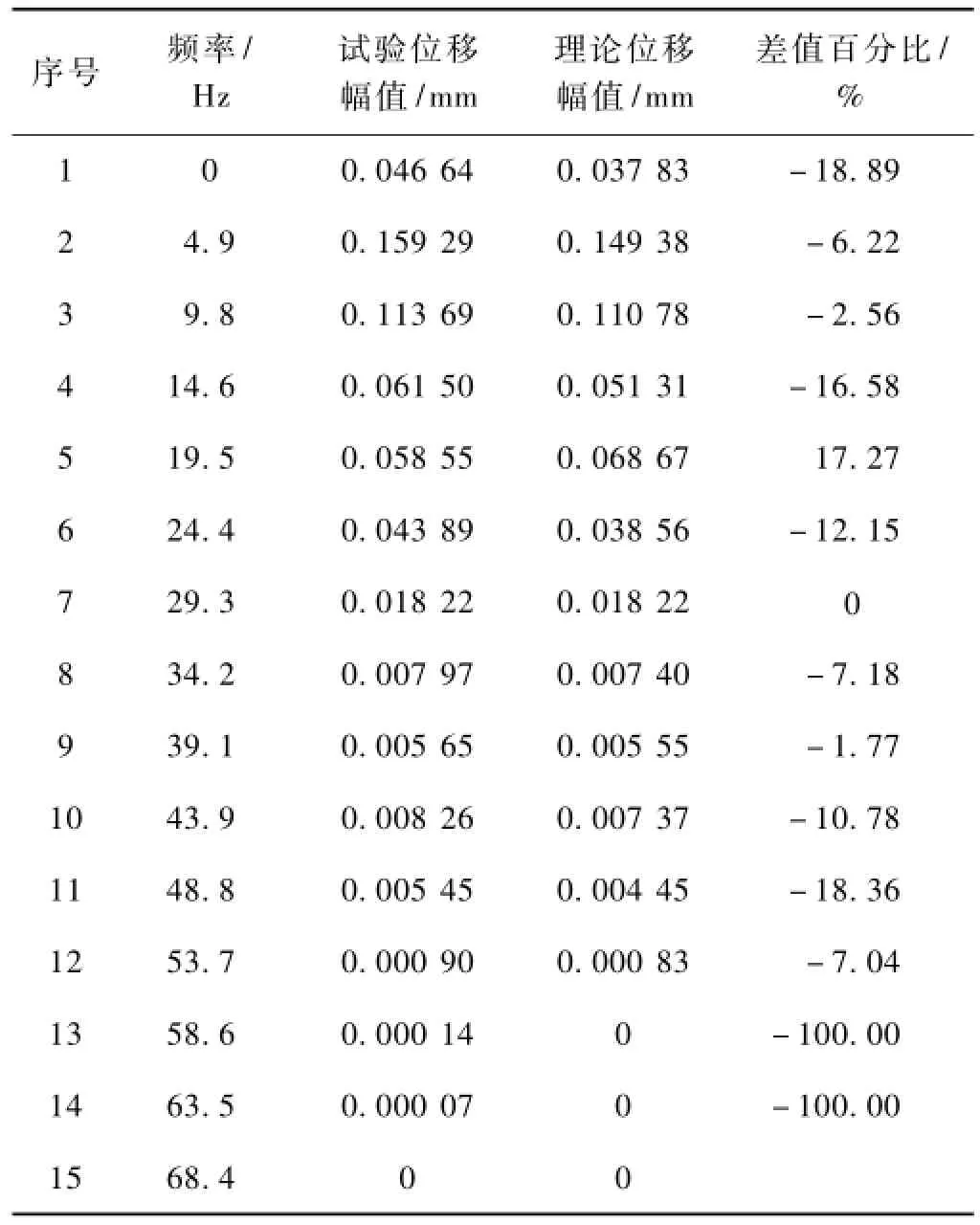
表3 试验位移幅值谱与理论幅值谱对比

由表3可知，剔除绝对值较小的情况，试验位移幅值和理论位移幅值差值百分比不大于20%。

对试验钢轨垂向位移幅值谱和理论计算钢轨垂向位移幅值谱做成对样本T检验［8］，试验和理论位移幅值统计量见表4，检验结果见表5。

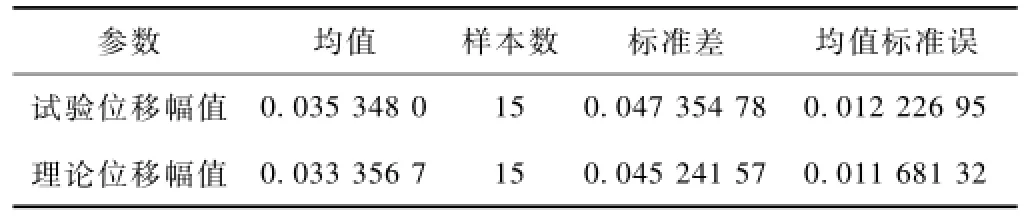
表4 试验和理论位移幅值统计量

从表5的检验结果可以看出，试验位移幅值和理论位移幅值的Pearson相关系数为0.995，因此可以得出试验位移幅值和理论位移幅值的变化趋势大体一致。另外表5给出了试验位移幅值和理论位移幅值的均值、标准差、均值标准误、95%的置信区间以及T检验分数、自由度和显著性水平(双侧)。由于试验位移幅值和理论位移幅值的配对T检验显著性水平(双侧)为0.151，超过0.05，所以可以认为试验位移幅值和理论位移幅值之间没有显著差异，即可以认定此次试验所测得的钢轨垂向位移和理论计算所得的钢轨垂向位移相吻合，从而认定此次试验数据是正确的。

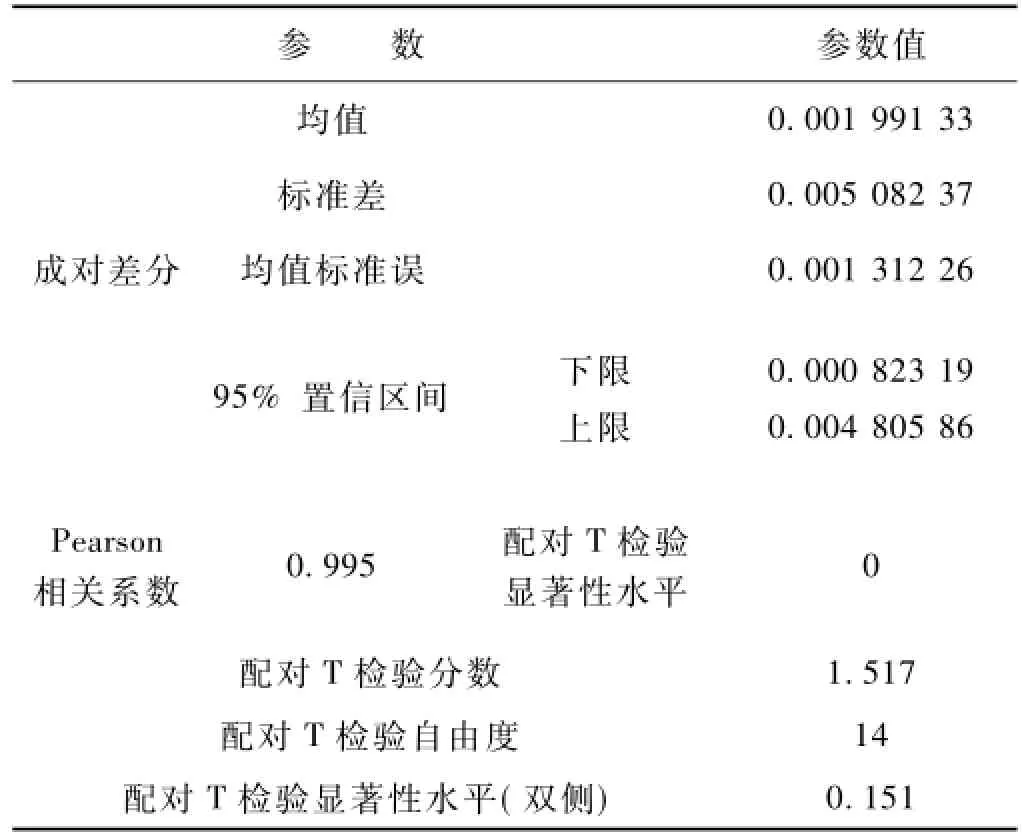
表5 试验和理论位移幅值检验结果

3 结语

在轨道工程测试过程中，由于各种各样的原因，测试数据的正确性会受到影响。本文通过构建有限元模型，利用垂直力的1/3倍频程作为激励谱推导出钢轨垂向位移的幅值谱，并与实际测试所获得的垂向位移幅值谱作比较，使得垂直力与钢轨垂向位移之间相互佐证，从而验证了测试数据的正确性。本文所选取的示例是通过力激励谱得到位移响应谱，同理，力谱、位移谱、加速度谱之间均可以相互佐证。

［1］胡广书.数字信号处理［M］.北京:清华大学出版社，2007.

［2］王济，胡晓.MATLAB在振动信号处理中的应用［M］.北京:中国水利水电出版社，2006.

［3］杨福生.随机信号分析［M］.北京:清华大学出版社，1990.

［4］李成辉.轨道［M］.成都:西南交通大学出版社，2011.

［5］郝瀛.铁道工程［M］.北京:中国铁道出版社，2000.

［6］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007.

［7］王勖成，邵敏.有限单元法基本原理和数值方法［M］.北京:清华大学出版社，1997.

［8］师义民.数理统计［M］.北京:科学出版社，2009.

(责任审编李付军)

U213.2+12

A

10.3969/j.issn.1003-1995.2015.05.36

1003-1995(2015)05-0144-03

2015-01-19;

2015-03-11

徐中秋(1989—)，男，江西广丰人，硕士研究生。