船舶气囊下水过程计算的程序设计

朱珉虎 朱 辉

（1.济南昌林气囊容器厂有限公司 济南250023；2.上海二手车信息服务有限公司 上海200000）

引 言

船舶气囊下水技术是我国具有自主知识产权的一项创新技术，自从20世纪80年代初推出以来，迅速取代传统的滑道下水技术而在中小型船厂普及，并扩展到大型船舶和海洋平台下水。目前正在从中国走向世界，说明这种下水技术具有取代其他下水技术的魅力。

对于大型船舶来说，为了确保其安全性，原有的手工计算方法已不能满足需要，必须编制计算机程序来处理大量数据，提高计算精度。我们从2006年开始这项工作，先解析建模、然后着手进行程序设计，于2009年完成了第一个版本计算机程序（V1.0，2009）的设计开发。

程序开发以后，需要有一个使用和发现问题的过程。相对来说，第一版的功能是比较简单的，只能适用于气囊下水早期使用的模式，当初针对的船型是30 000载重吨以下的船型，这类船舶的下水质量不足10 000 t。气囊的布置方式为等间距、统一的气囊尺度，如今来看，已经不能完全适应大型船舶下水的要求。

2010年12月3日，浙江舟山正和造船有限公司用气囊下水了一艘载重量70 000 t的散货船（见图1），这在船舶气囊下水的历史上是一个里程碑。不仅仅是因为它的下水质量跃上万吨台阶，开创了大型船舶下水的新纪元。主要是因为在这艘船上，使用了一系列突破性的气囊下水技术，例如气囊对置布置形式、不等间距布置形式，并实测了气囊下水对结构强度的影响。

图1 70 000 载重吨散货船气囊下水

使用过程中冒出来的问题以及一些新的需求，促使我们在2011年进行一次较大的增补和修改，从原来的4个模块增加到8个模块。即增添了所谓的第二种模式：气囊不等间距布置和允许采用多种规格的气囊进行拼接，即成为第二版（V2.0，2011）。

从第二版到第三版，又经历一个飞跃。首先是增加两个很重要的功能模块。其一是气囊下水冲程的计算，称为“动力学计算模块”。这个模块不仅计算出气囊作用力对船的推动作用，而且计算出水的阻力。在作用力计算正确的基础上，算出瞬时加速度、速度和经过每一区段所需的时间，得到最后的冲程。其二是结构力学计算模块。这个模块能够计算出重力曲线、剪力曲线、弯矩曲线，用于校验指定剖面的应力。

2014年，我们以比较完善的第三版（V3.0，2013）向国家版权局申请软件著作权，获得登记证书。这是气囊下水领域第一个实用的计算机软件。

1 气囊下水过程的描述

气囊下水过程是指船舶到达气囊下水的指定地点，并且全部气囊已经按设计要求的压力充足气。这时，释放或砍断牵住船舶的钢缆，船舶在重力的作用下，沿着斜坡依赖于气囊的滚动向水面下行。

开始时，船舶尾端呈悬臂状下坠向水面伸出，船尾纵倾增加，尾部接近坡道末端的几个气囊压扁，船体重心下挫，在船尾接触水面前会保持这种趋势。这个阶段，船体的重量全部由气囊承担。

船尾入水后产生浮力，抑制尾部继续下沉。随着入水体积的增加，尾部逐渐上抬，船体纵倾角减小，此时船体的质量由气囊和浮力分担。这个过程直到船首离开坡道终端，全部气囊逸出结束。此时船舶质量全部由浮力托起，称为“全浮”。

从船体解脱钢缆的约束开始运动到船舶全部浮起的过程称为“全浮过程”。本文就是介绍气囊下水全浮过程的计算方法和程序设计，这是整个气囊下水计算程序最核心的部分，包括需要输入的参数、计算使用的数学模型、程序设计的原理和输出参数等；揭示船舶在气囊下水过程中的受力状态、瞬时的姿态变化、气囊内部压力的变化等；既是船舶气囊下水过程的预演，也是进行其他受力计算的基础。

2 输入参数

2.1 船型参数

下列参数不可缺省：

（1）两柱间长LBP；

（2）下水重量W；

（3）重心纵向位置LCG：重心距舯的距离，舯前为正，舯后为负。

2.2 船底的型值

常见的运输船船底形状如图2所示，按20等分站线将宽度型值输入。

图2 船底形状

2.3 邦戎曲线数据

邦戎曲线数据是用来计算船体入水部分浮力和浮心位置的，可按设计院提供的数据用Excel表格的形式输入。

2.4 环境参数

环境参数是气囊下水计算的重要参数之一。如图3所示，主要有上坡道倾角β1、下坡道倾角β2、下坡道的水平长度SR、水深h1、上坡道末端水深h2、船舶尾柱距离上坡道末端的位置XAP。

2.5 气囊参数

气囊参数一般是在船舶下水前用气囊把船体抬起，然后拆除支墩阶段就设定的。这个阶段在气囊下水术语中称为“起墩阶段”。气囊参数包括气囊直径D、气囊长度L、气囊充气压力p、船舶重心处的气囊工作高度HG等。

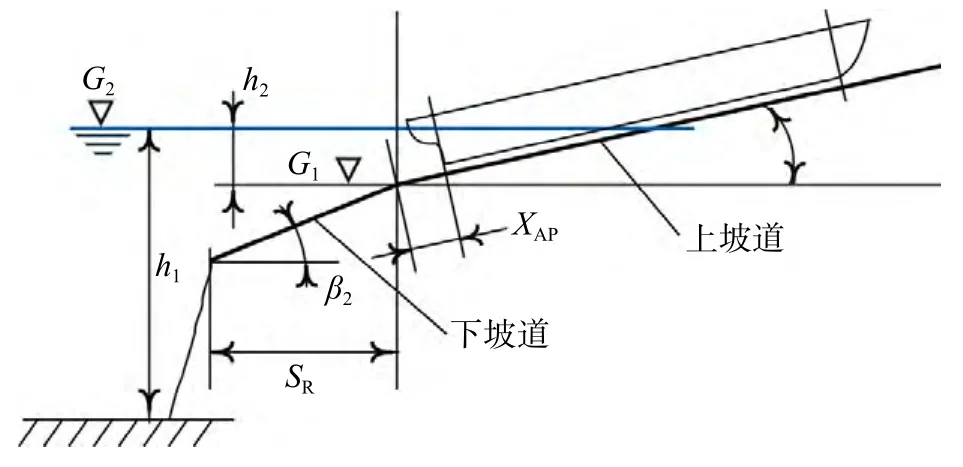
图3 环境参数

3 计算方法和数学模型

船底下的气囊可视为弹性支座，只能承压而不能受拉，故称为接触元。作为弹性支座的气囊像弹簧一样能够伸张和压缩，当工作高度小于气囊直径时，它始终对船体提供支承力，其刚度呈非线性。

由于气囊下水时，船舶是在弹性垫上作三维方向的运动：x方向是行程；z方向是垂向升降；还有一个方向是绕重心轴旋转。所以必须用包括弹性力学在内的动态数学模型来模拟气囊下水过程，建立完全新颖的气囊下水计算方法［1］。

3.1 平衡方程

3.1.1 起始状态

气囊下水的起始状态如图4所示。

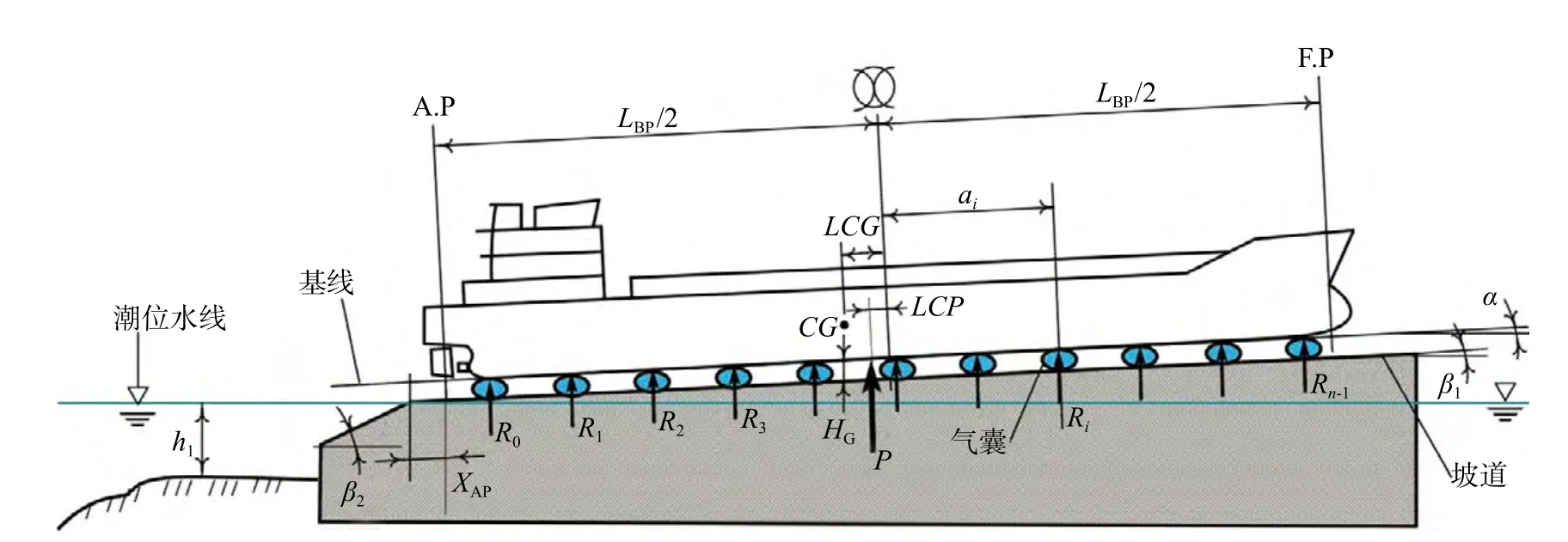
图4 气囊下水起始状态

（1）垂直方向力的平衡方程

作用在垂直方向的力主要有重力W和气囊反压力的垂向分力PZ。我们取向上的力为正，向下的力为负，于是：

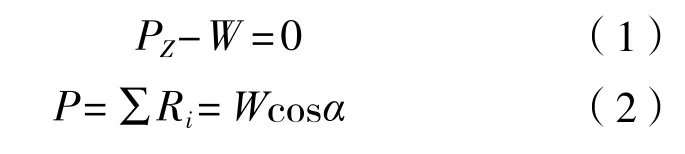
式（2）中的P为气囊对船底正压力的合力。如果不考虑方向，用W的绝对值来取代P的值仅会引起微小误差。

（2）力矩平衡方程

相对于船舯剖面来说，引起船纵倾的力矩主要有重力矩和气囊反力引起的力矩，顺时针为正，逆时针为负，达到平衡时为：

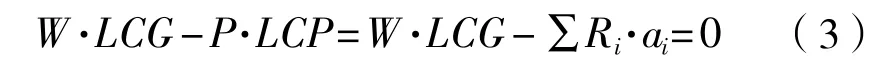
式中：W为重力，kN；因重力向下为负值；α为船底基平面与水平面的夹角，（°）；α通常为负值；Ri为各个气囊的载力，kN；P为气囊对船底正压力的合力，kN；LCP为气囊压力合力距舯的距离，m；LCG为船舶重心距舯的距离，m；ai为各个气囊相对于船舯的位置，m。

3.1.2 尾部入水后

船舶沿着坡道的方向行进X行程后，尾部进入水中，产生浮力（如图5所示），上述力和力矩的平衡方程有所改变。

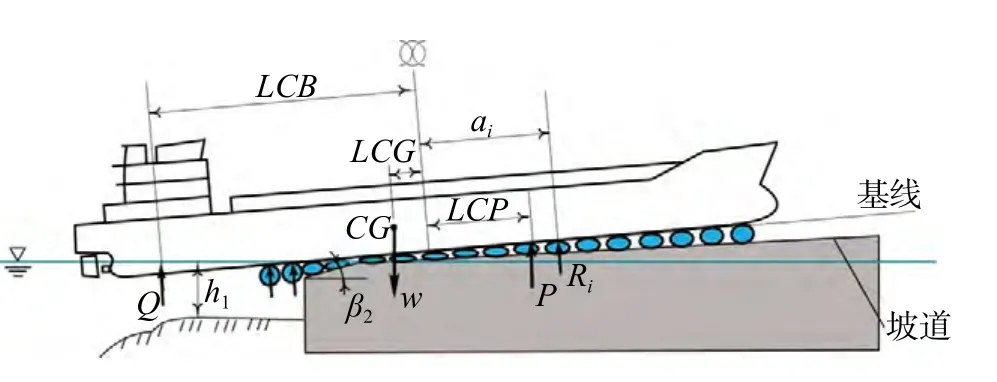
图5 尾部入水后状态

（1）垂直方向力的平衡方程

作用在垂直方向的力主要有重力W、气囊反压力的垂向分力PZ以及尾部水的浮力Q：

（2）力矩平衡方程

相对于船舯剖面来说，引起船纵倾的力矩除重力矩和气囊反力矩之外，增加了浮力矩，顺时针为正，逆时针为负，达到平衡时为：

3.2 气囊的刚度

在船舶气囊下水过程中，气囊的作用就好似一根弹簧。气囊载力的计算主要是解决气囊的刚度问题。刚度是载荷与变形量的比，充以一定压力空气的气囊当压缩高度改变时，其压缩反力会随之发生变化，其刚度为：

式中：G为气囊的刚度，kN/m；R为气囊的承载力，kN；Z为气囊的垂直压缩量，m。

气囊刚度是进行气囊下水计算和船体结构强度计算所必需的基础数据，以下通过推导，提出计算气囊刚度的理论公式。

分析气囊压缩反力（承载力）的增量是由以下两部分组成的：

其一是接触面积的改变量，在平行面压缩的情况下，接触面积的改变量基本与压缩量Z成线性关系；其二是气囊内压的改变量，根据我们所做的试验结果，它是非线性的，而且因气囊物理特性的不同而不同。

在船舶气囊下水过程中，气囊的压缩量不断改变，气囊内气体质量不变，随着气囊容积的变化，气囊内气体的压力p会发生相应的改变。设初始状态下的工作高度为H1，则当气囊在垂向变形dZ时，其工作高度变为H2，气囊的载力变为：

于是得到气囊刚度的计算公式：

图6［3］是气囊压缩性能曲线，当气囊处于低压缩比时（≤40%），p曲线的变化较缓，基本上与压缩量成线性关系。但当气囊处于高压缩比阶段时，内压p的变化曲线变陡；此时，即使压缩量略有改变，p的改变量也不可忽视，呈非线性关系。我们把它回归成一条指数曲线：

式中：b、m是回归系数（为常量）。

图6 气囊压缩性能曲线

于是，式（9）可写成一般形式：

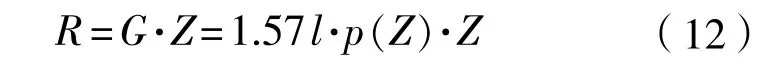
4 程序设计

程序设计是对实船下水过程的仿真。

4.1 确认初始状态

船舶下水开始时的状态称为“初始状态”。此时船已经承载在气囊上，各个气囊已经充气，其内压为pi0，距船舯的距离为ai0，船重心处船底离地面高度为HG0，船尾柱距上坡道末端距离为XAP。此时可通过平衡式（2）和式（3）求得船相对于坡道的纵倾角τ（通常τ≠0），有时为了下水方便，施工队会将船故意向尾倾斜一个角度。此时船龙骨平面相对于水平面的倾角α：

4.2 全浮过程计算

气囊下水过程的计算划分成许多步来进行，每一步的步长称为Step，则第I步的船舶行程JS：

船舶航行一段距离后，各种参数都发生改变，原来的平衡被打破。船舶会产生坐沉和绕重心旋转，以达到新的平衡。

计算步骤、方法和数学模型介绍如下：

（1）首先要确定各个气囊的新位置

气囊的运动速度仅为船舶行进速度之半，故气囊相对于船舯的位置可按下式求得：

（2）确定各个气囊的工作高度Hi

首先假定HG与τ不变，即采用上一步计算求得的HG和τ，按下式计算各个气囊的工作高度Hi：

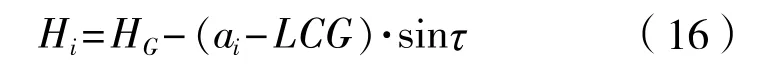
这里还要注意气囊相对于上坡道末端的位置Xi。船舶未启动前，所有的气囊位置都位于上坡道终端的上方，气囊相对于终端的距离为正值。当船向下行进一段距离后，尾部的气囊也跟着下行，当越过终端之后，气囊相对于终端的距离变为负值。此时，上坡道面对气囊的约束消失。如果没有下坡道，而水深又足够的话，这个气囊则不受约束（压缩）成自由状态了（即Hi=D）。如果有下坡道，气囊的工作高度则按下式计算：

（3）计算各个气囊的载力Ri和载力对舯力矩MTi

气囊的工作高度改变之后，内部压力也发生变化。各个气囊的载力Ri可利用式（12）求得。载力对舯力矩MTi可按下式求得：

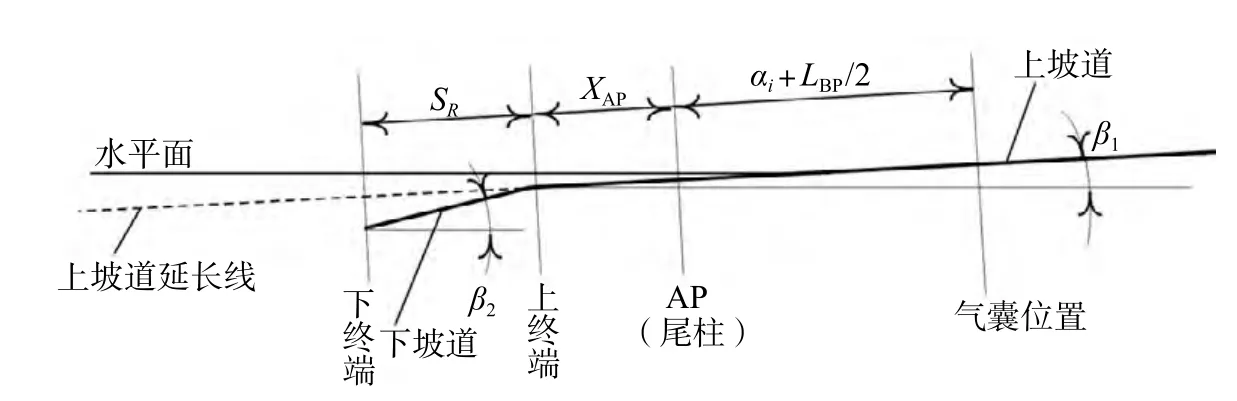
图7 气囊与终端的相对位置

（4）浮力和浮心位置的计算

图8显示一艘倾斜的船沿坡道下到水中，尾部产生了浮力。浮力和浮心位置的计算用到了“邦戎曲线数据”，其计算方法可在相关文献中查到［2］。

图8 浮力计算

计算步骤和方法如下：

（1）计算尾吃水TA：

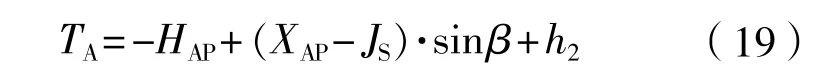
（2）求水线长度l0及与龙骨线交点的站号jm：当船之尾吃水变为正值，而首吃水仍为负值时，可求得水线与龙骨线交点距尾柱的长度l0：

（注意：公式中出现负号是因为α为负值之故。）

此长度可转化为站号，即水线与龙骨线交点的站号jm：

jm若大于j站号而小于j+1站号，则可用它来取代j+1站号，以此类推作为浮力计算的结束站点。在这个站点，吃水Tjm=0，横剖面面积Sjm=0，距船舯的距离：

（3）计算各站线处的吃水Tj：

（4）计算各站线处的横剖面面积Sj和距船舯的距离dj：

各横剖面面积距船舯的距离dj按下式计算：

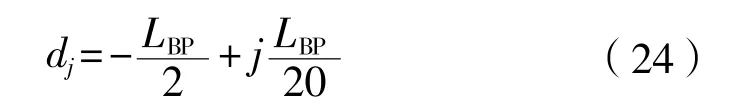
（5）计算浮力Q和浮心距船舯的距离LCB：

程序用梯形法计算排水体积▽，再乘以水的密度ρ和重力加速度g，即能得到浮力Q：

4.3 如何求平衡

在船舶气囊下水过程计算中求平衡是非常重要的。船舶在运动过程中是自动平衡的，包括绕重心旋转和坐沉。若我们的计算状态未达到平衡状态，则所有的计算结果都是不准确的。所谓平衡状态，从数学概念来讲，就是垂向力之和以及对船舯力矩之和达到一个极小量，工程上常用基准值的5%作为允许误差，因此我们可以把垂向力和纵倾力矩平衡方程写成以下不等式形式：

满足上述不等式即算达到平衡状态。

船每行进一步，我们在计算时先假定船相对于坡道面的姿态没有变化，即τ和HG处于前一步终结时的平衡状态，但气囊相对于船舯的位置已有改变，由新的ai计算出Hi、pi、Ri等一系列数据，以及尾吃水、浮力、LCB等数据。此时，前一步的平衡状态已经打破，即不再满足式（27），需对倾角τ和离地面高度HG进行调整才能达到新的平衡状态。

（1）调整重心处船底离地面高度HG

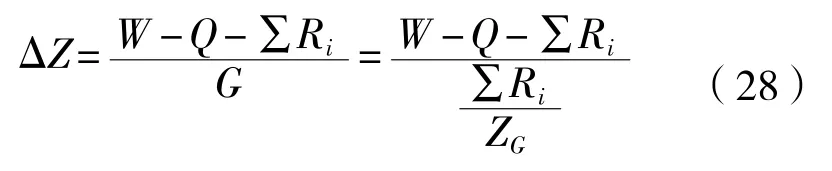
新的重心处船底离地面高度HG_new

求得新的重心处船底离地面高度HG_new后，再按以前的计算步骤用新的HG_new代入重新计算一遍，包括尾吃水、浮力、浮心纵向位置LCB等，使数据全面刷新，接着进入下一步骤：调整船舶的纵倾角τ。

（2）调整船舶的纵倾角τ

经过上一步骤，数据全面刷新之后，相信在满足式（27）方面有了显著改善。倘若仍不满足的话，就要调整船舶的纵倾角τ了。即令

5 输出数据

全浮过程计算的结果主要形成两类数据。一类是气囊内压在下水过程中不断变化的数据（参阅下页表1）。它的作用是能看到每一只气囊在哪一行程（步）达到最大压力；这个最大压力有多大？是否会产生爆破？在气囊标准中规定了各种型号气囊要求达到的爆破压力最小值［3-4］。只要不超过这个规定的爆破压力值，就可认为是安全的。表中压力为0的气囊说明在所处的行程已经不起作用。

从表1中可以看出，在下水过程中，压力变化比较大的仅是靠近尾部的0～17号气囊，第17号气囊向首的气囊压力在下水过程中的变化缓和，均处于稳中有降的状况。图9画出1～17号气囊内压在船舶气囊下水过程中的变化曲线。最大内部压力系9号气囊在行程90 m处出现，其值在250 kPa左右，远小于D=1.5 m六层气囊要求的最小爆破压力390 kPa，说明是十分安全的。

图9 某30 000载重吨级散货船气囊内压变化曲线（计算结果）

另一类数据是有关船的动态参数的，如行程、船舶重心离地面高度、纵倾角、首尾吃水、浮力、气囊承载力及其作用力中心的纵向位置等。这些数据汇总在表2中，称为全浮过程计算结果汇总表。

表1 某30 000载重吨级船型下水过程中的气囊内压变化数据 kPa

表2的内容说明如下：

（1）表中第1列是步数，第2列是行程。从表中可以看出全浮过程经20步计算后结束，总行程为224 m。此时气囊的载力R为0，达到全浮状态。

（2）表中第3列是船舶重心处船底离地面的高度HG；第6列是船舶尾柱处船底离地面高度HAP，都是相对于主坡道表面而言的，出现负值则表示在主坡道的延长线之下。这种情况只可能出现在该处已越出了主坡道终端后，主坡道的延长线成为一个参考平面，见图10中的虚线。

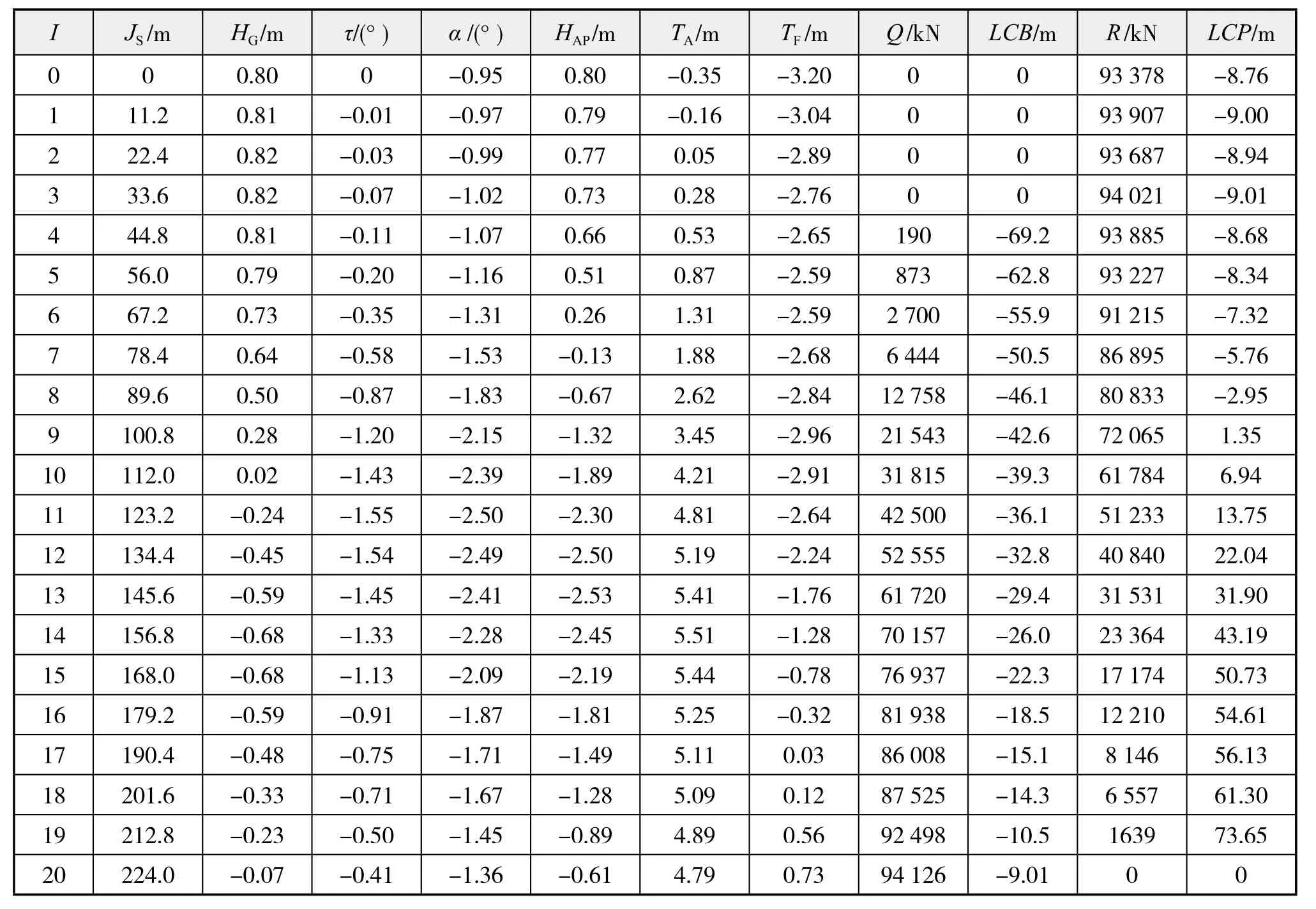
表2 某30 000载重吨级散货船全浮过程计算结果汇总表

图10 某30 000载重吨级散货船气囊下水全浮过程曲线

（3）第7、8两列是尾吃水TA和首吃水TF，负值表示在水平面以上，尚未入水。最底下一行显示的首、尾吃水恰好就是空船的静浮吃水。从表列数据来看，最大的尾吃水出现在第14步时，达到5.658 m，比空船尾吃水4.902 m大0.756 m，所以下水水域的水深应比计算得到的空船静浮吃水大一些，才能确保下水安全。

图10是根据表2中数据绘制的曲线图。图中可以看到气囊载力、浮力曲线的变化情况、船舶纵倾角的变化情况以及重心处船底离上坡道面高度和相对于水平面的高度。图中还画出了上坡道和下坡道的位置以及坡道参考线的位置（图中纵坐标的高度标尺为每格0.4 m）。

6 结 论

（1）针对气囊下水的特点和过程的剖析，对气囊下水过程和环境参数进行描述，建立气囊下水过程计算的数学模型，并推导气囊刚度的计算公式，为编制计算机程序奠定了基础。

（2）按照建立的数学模型，编制完成计算机程序，通过一艘30 000载重吨级船型的计算，输出的结果符合预期要求。本程序计算的结果可作为其他计算的基础，如动力学计算和结构强度校核。

（3）本程序输出的结果可供进行安全评估、方案比较以及对环境参数的考量，以便制定应急预案和方案的改进。

（4）船舶气囊下水的技术正在发展，还有许多未知领域，随着应用领域的拓展和测试技术的进步，本程序将不断改进以适应新的需求。

［1］ 朱珉虎，孙菊香.船舶气囊纵向下水计算方法的研究［J］.船舶，2009（3）：39-44.

［2］ 中国船舶工业总公司.船舶设计实用手册（总体分册）［M］.北京：国防工业出版社，1998.

［3］ ISO 14409.Ships and marine technology-Ship launching air bags［S］.2011.

［4］ 王绍清，朱珉虎.高承载力多层揉压气囊的研制与使用［J］.造船技术，2006（5）：27-31.